Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 2 - Hình học 9 — Không quảng cáo

Đề bài

Cho đường tròn (O). Hai dây AB và CD song song với nhau. Biết $AB = 30cm, CD = 40cm$, khoảng cách giữa hai dây là 35cm. Tính bán kính đường tròn (O).

Lời giải chi tiết

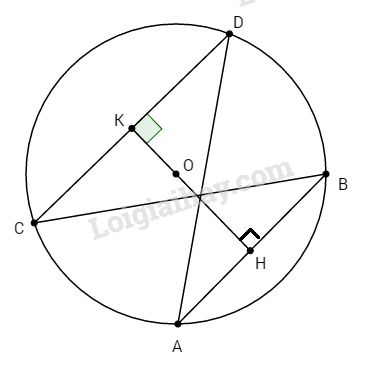
Kẻ $OH ⊥ AB$, ta có:

$HA = HB = {{AB} \over 2} = {{30} \over 2} = 15\,\left( {cm} \right)$ (định lí đường kính dây cung)

Mặt khác: vì AB // CD (gt)

nên $OH ⊥ CD$ tại K, ta có:

$KC = KD = {{CD} \over 2} = {{40} \over 2} = 20cm$

Khi đó các tam giác AHO và CKO vuông. Theo định lí Pi-ta-go :

$\eqalign{  & A{H^2} + O{H^2} = O{A^2}\left( { = {R^2}} \right)  \cr  & C{K^2} + O{K^2} = O{C^2}\left( { = {R^2}} \right)  \cr  &  \Rightarrow A{H^2} + O{H^2} = C{K^2} + O{K^2}\,\left( * \right) \cr}$

Đặt $OK = x ⇒ OH = 35 – x$ (**)

Thay (**) vào (*), ta có:

$\eqalign{  & {15^2} + {\left( {35 - x} \right)^2} = {20^2} + {x^2}  \cr  &  \Leftrightarrow 225 + 1225 - 70x + {x^2} = 400 + {x^2}  \cr  &  \Leftrightarrow 70x = 1050 \Leftrightarrow x = 15 \cr}$

Xét tam giác vuông CKO ta có:

$C{O^2} = O{K^2} + C{K^2}$ (định lí Pi-ta-go)

hay ${R^2} = {15^2} + {20^2} \Rightarrow {R^2} = 625$

$\Rightarrow R = 25\,\left( {cm} \right)$

Vậy bán kính đường tròn là 25cm.