Đề kiểm tra 15 phút - Đề số 8 - Bài 8 - Chương 2 - Hình học 9 — Không quảng cáo

Đề bài

Cho hình bình hành ABCD ($AB > AD$). Vẽ đường tròn tâm A bán kính AD, đường tròn (A) cắt AB tại E. Vẽ đường tròn tâm B bán kính BE, đường tròn (B) cắt đường thẳng DE tại F. Chứng minh đường tròn (A; AD) và (B; BE) tiếp xúc với nhau và ba điểm F, B, C thẳng hàng.

Lời giải chi tiết

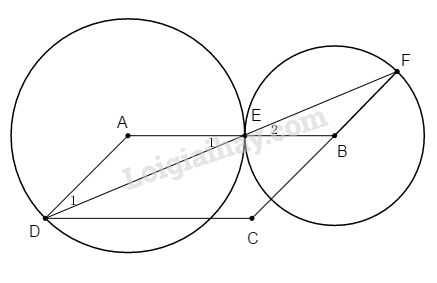
Ta có: $AB = AE + EB\; (d = R + R’)$

$⇒ (A; AD)$ và $(B; BE)$ tiếp xúc ngoài với nhau tại E.

Ta có ∆ADE cân tại A ($AD = AE = R$) $\Rightarrow {\widehat D_1} = {\widehat E_1}$

Tương tự ∆EBF cân tại B

$\Rightarrow \widehat F = {\widehat E_2},$ mà ${\widehat E_1} = {\widehat E_2}$ (đối đỉnh)

$\Rightarrow {\widehat D_1} = \widehat F.$ Do đó AD // BF. Lại có AD // BC (gt)

Theo tiên đề Ơ-clit : BF và BC phải trùng nhau hay F, B, C thẳng hàng.