Đề kiểm tra 15 phút - Đề số 9 - Bài 1 - Chương 1 - Hình học 9 — Không quảng cáo

Đề bài

Cho \(∆ABC\) vuông tại A, M là trung điểm của AC. Vẽ MD vuông góc với cạnh huyền \(BC\; (D ∈ BC)\). Chứng minh : \(A{B^2} = B{D^2} - C{D^2}\)

Lời giải chi tiết

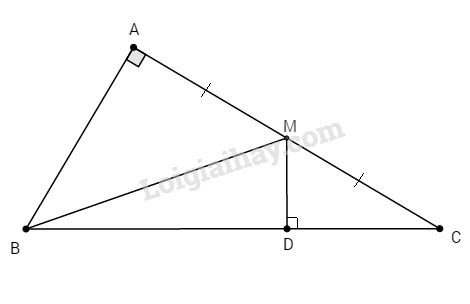
Nối BM. Xét tam giác BDM vuông ta có:

\(B{D^2} = B{M^2} - M{D^2}\) (định lí Pi-ta-go)

Xét tam giác CDM có \(D{C^2} = M{C^2} - M{D^2}\) (định lý Pi-ta-go)

\( \Rightarrow B{D^2} - D{C^2} = B{M^2} - M{C^2}\) (1)

Xét tam giác vuông BAM ta có:

\(A{B^2} = B{M^2} - A{M^2}\) (2) (định lí Pi-ta-go)

Lại có \(MA = MC\) ( vì M là trung điểm của AC)

\( \Rightarrow B{D^2} - D{C^2} = A{B^2}\) (đpcm)