Đề kiểm tra giữa học kì 2 Toán 4 Cánh diều - Đề số 4
Số thích hợp điền vào chỗ chấm 28 cm2 10 mm2 = ....... mm2 là ... Sân trước nhà Mai có chiều dài 14 m và chiều rộng 12 m. Bố Mai muốn sử dụng các viên gạch hình vuông cạnh 4 dm để lát nền sân.
Đề bài
-
A.
$\frac{5}{6}$
-
B.
$\frac{2}{3}$
-
C.
$\frac{5}{3}$
-
D.
$\frac{1}{3}$
Rút gọn phân số $\frac{{28}}{{42}}$ ta được phân số tối giản là:
-
A.
$\frac{{14}}{{21}}$
-
B.
$\frac{4}{7}$
-
C.
$\frac{6}{7}$
-
D.
$\frac{2}{3}$
Trong các phân số dưới đây, phân số nhỏ nhất là:
-
A.
$\frac{7}{8}$
-
B.
$\frac{5}{6}$
-
C.
$\frac{{47}}{{48}}$
-
D.
$\frac{{13}}{{16}}$
-
A.
1 hình
-
B.
2 hình
-
C.
3 hình
-
D.
4 hình
Số thích hợp điền vào chỗ chấm 28 cm 2 10 mm 2 = ....... mm 2 là:
-
A.
2 810
-
B.
28 100
-
C.
281 000
-
D.
2 801
Sân trước nhà Mai có chiều dài 14 m và chiều rộng 12 m. Bố Mai muốn sử dụng các viên gạch hình vuông cạnh 4 dm để lát nền sân. Hỏi bố Mai cần chuẩn bị bao nhiêu viên gạch loại đó để vừa đủ lát kín nền sân. (Diện tích phần mạch vữa không đáng kể)
-
A.
672 viên
-
B.
168 viên
-
C.
525 viên
-
D.
1 050 viên
Ngày thứ Bảy, anh Nam về thăm quê. Giờ thứ nhất anh đi được $\frac{5}{{12}}$ quãng đường. Giờ thứ hai anh đi hơn giờ thứ nhất $\frac{1}{4}$ quãng đường. Hỏi giờ thứ hai anh Nam đi được bao nhiêu phần quãng đường?
-
A.
$\frac{1}{2}$ quãng đường
-
B.
$\frac{2}{3}$ quãng đường
-
C.
$\frac{7}{{12}}$ quãng đường
-
D.
$\frac{3}{4}$ quãng đường
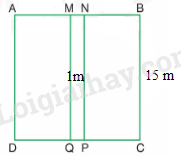
Bác Cường trồng hoa trên mảnh đất hình vuông có cạnh 15 m, ở giữa là lối đi hình chữ nhật có chiều rộng 1 m như hình bên. Diện tích trồng hoa là:
-
A.
15 m 2
-
B.
225 m 2
-
C.
195 m 2
-
D.
210 m 2
Lời giải và đáp án
-
A.
$\frac{5}{6}$
-
B.
$\frac{2}{3}$
-
C.
$\frac{5}{3}$
-
D.
$\frac{1}{3}$
Đáp án : C
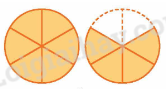
Phân số chỉ số phần đã tô màu có tử số là số phần được tô màu và mẫu số là tổng số phần bằng nhau.
Phân số chỉ số phần đã tô màu trong hình bên là $\frac{{10}}{6}$ hay $\frac{5}{3}$.
Rút gọn phân số $\frac{{28}}{{42}}$ ta được phân số tối giản là:
-
A.
$\frac{{14}}{{21}}$
-
B.
$\frac{4}{7}$
-
C.
$\frac{6}{7}$
-
D.
$\frac{2}{3}$
Đáp án : D
Cách rút gọn phân số:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản
Ta có $\frac{{28}}{{42}} = \frac{{28:14}}{{42:14}} = \frac{2}{3}$
Trong các phân số dưới đây, phân số nhỏ nhất là:
-
A.
$\frac{7}{8}$
-
B.
$\frac{5}{6}$
-
C.
$\frac{{47}}{{48}}$
-
D.
$\frac{{13}}{{16}}$
Đáp án : D
Quy đồng mẫu số các phân số rồi so sánh để tìm phân số nhỏ nhất.
$\frac{7}{8} = \frac{{7 \times 6}}{{8 \times 6}} = \frac{{42}}{{48}}$
$\frac{5}{6} = \frac{{5 \times 8}}{{6 \times 8}} = \frac{{40}}{{48}}$
$\frac{{13}}{{16}} = \frac{{13 \times 3}}{{16 \times 3}} = \frac{{39}}{{48}}$
Ta có $\frac{{39}}{{48}} < \frac{{40}}{{48}} < \frac{{42}}{{48}} < \frac{{47}}{{48}}$
Vậy phân số nhỏ nhất trong các phân số đã cho là $\frac{{13}}{{16}}$
-
A.
1 hình
-
B.
2 hình
-
C.
3 hình
-
D.
4 hình
Đáp án : C
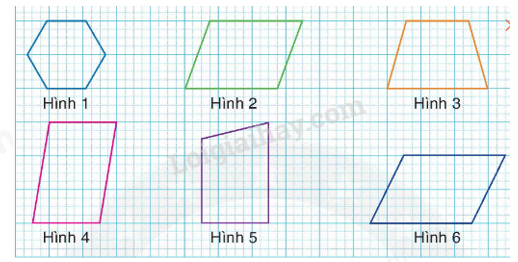
Hình bình hành có 2 cặp cạnh đối diện song song và bằng nhau.
Có 3 hình bình hành là: hình 2, hình 4, hình 6.
Số thích hợp điền vào chỗ chấm 28 cm 2 10 mm 2 = ....... mm 2 là:
-
A.
2 810
-
B.
28 100
-
C.
281 000
-
D.
2 801
Đáp án : A
Áp dụng cách đổi: 1 cm 2 = 10 mm 2
Ta có 28 cm 2 10 mm 2 = 2 800 mm 2 + 10 mm 2 = 2 810 mm 2
Sân trước nhà Mai có chiều dài 14 m và chiều rộng 12 m. Bố Mai muốn sử dụng các viên gạch hình vuông cạnh 4 dm để lát nền sân. Hỏi bố Mai cần chuẩn bị bao nhiêu viên gạch loại đó để vừa đủ lát kín nền sân. (Diện tích phần mạch vữa không đáng kể)
-
A.
672 viên
-
B.
168 viên
-
C.
525 viên
-
D.
1 050 viên
Đáp án : D
- Tìm diện tích sân = chiều dài x chiều rộng
- Tìm diện tích viên gạch = cạnh x cạnh
- Tìm số viên gạch cần mua
Diện tích sân nhà Mai là: 14 x 12 = 168 (m 2 ) = 16 800 dm 2
Diện tích mỗi viên gạch là: 4 x 4 = 16 (dm 2 )
Bố Mai cần chuẩn bị số viên gạch là: 16 800 : 16 = 1 050 (viên gạch)
Ngày thứ Bảy, anh Nam về thăm quê. Giờ thứ nhất anh đi được $\frac{5}{{12}}$ quãng đường. Giờ thứ hai anh đi hơn giờ thứ nhất $\frac{1}{4}$ quãng đường. Hỏi giờ thứ hai anh Nam đi được bao nhiêu phần quãng đường?
-
A.
$\frac{1}{2}$ quãng đường
-
B.
$\frac{2}{3}$ quãng đường
-
C.
$\frac{7}{{12}}$ quãng đường
-
D.
$\frac{3}{4}$ quãng đường
Đáp án : B
Số phần quãng đường giờ thứ hai anh Nam đi được = Số phần quãng đường giờ thứ nhất đi được + $\frac{1}{4}$ quãng đường
Giờ thứ hai anh Nam đi được số phần quãng đường là:
$\frac{5}{{12}} + \frac{1}{4} = \frac{8}{{12}} = \frac{2}{3}$ (quãng đường)
Bác Cường trồng hoa trên mảnh đất hình vuông có cạnh 15 m, ở giữa là lối đi hình chữ nhật có chiều rộng 1 m như hình bên. Diện tích trồng hoa là:

-
A.
15 m 2
-
B.
225 m 2
-
C.
195 m 2
-
D.
210 m 2
Đáp án : D
- Tìm diện tích mảnh đất hình vuông = cạnh x cạnh
- Tìm diện tích lối đi = chiều dài x chiều rộng
- Diện tích trồng hoa = diện tích mảnh đất hình vuông - diện tích lối đi
Diện tích mảnh đất hình vuông là: 15 x 15 = 225 (m 2 )
Diện tích lối đi là 15 x 1 = 15 (m 2 )
Diện tích để trồng hoa là: 225 – 15 = 210 (m 2 )
- Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
- Muốn trừ hai phân số có cùng mẫu số, ta lấy tử số của phân số thứ nhất trừ đi tử số của phân số thứ hai và giữ nguyên mẫu số.
a) $\frac{2}{9} + \frac{{11}}{{18}} = \frac{4}{{18}} + \frac{{11}}{{18}} = \frac{{15}}{{18}} = \frac{5}{6}$
b) $\frac{{11}}{{18}} - \frac{5}{{18}} = \frac{6}{{18}} = \frac{1}{3}$
c) $\frac{5}{{16}} + \frac{7}{8} + \frac{3}{4} = \frac{5}{{16}} + \frac{{14}}{{16}} + \frac{{12}}{{16}} = \frac{{31}}{{16}}$
d) $\frac{{41}}{{40}} - \frac{{17}}{{40}} = \frac{{41 - 17}}{{40}} = \frac{{24}}{{40}} = \frac{3}{5}$
Áp dụng cách đổi:
1 m 2 = 100 dm 2 = 10 000 cm 2
1 cm 2 = 100 mm 2
a) 3m 2 58 dm 2 = 358 dm 2
b) 9m 2 36 cm 2 = 90 036 cm 2
c) 80 070 mm 2 = 800 cm 2 70 mm 2
d) 2 050 cm 2 = 20 dm 2 50 cm 2
- Quy đồng mẫu số các phân số rồi so sánh
- Sắp xếp các phân số sau theo thứ tự từ lớn đến bé
Ta có $\frac{{15}}{{16}} < 1\,,\,\,\frac{{21}}{{32}} < 1\,,\,\,\frac{5}{8}\, < 1$ ; $\frac{3}{2} > 1$
$\frac{{15}}{{16}} = \frac{{15 \times 2}}{{16 \times 2}} = \frac{{30}}{{32}}$
$\frac{5}{8} = \frac{{5 \times 4}}{{8 \times 4}} = \frac{{20}}{{32}}$
Ta có $\frac{{30}}{{32}} > \frac{{21}}{{32}} > \frac{{20}}{{32}}$ nên $\frac{{15}}{{16}} > \frac{{21}}{{32}} > \frac{5}{8}$
Vậy các phân số sắp xếp theo thứ tự từ lớn đến bé là: $\frac{3}{2}$; $\frac{{15}}{{16}}$ ; $\frac{{21}}{{32}}$ ; $\frac{5}{8}$
- Tìm chiều dài = (tổng + hiệu) : 2
- Chiều rộng = Nửa chu vi – chiều dài
- Diện tích thửa ruộng = chiều dài x chiều rộng
- Số kg khoai thu được = Diện tích thửa ruộng : 36 x 95
Chiều dài của thửa ruộng là:
(102 + 6) : 2 = 54 (m)
Chiều rộng của thửa ruộng là:
54 – 6 = 48 (m)
Diện tích thửa ruộng là:
54 x 48 = 2 592 (m 2 )
Cả thửa ruộng thu hoạch được số ki-lô-gam khoai là:
2 592 : 36 x 95 = 6 840 (kg)
Đáp số: 6 840 kg khoai