Đề kiểm tra học kì 2 Toán 9 - Đề số 5
Đề bài
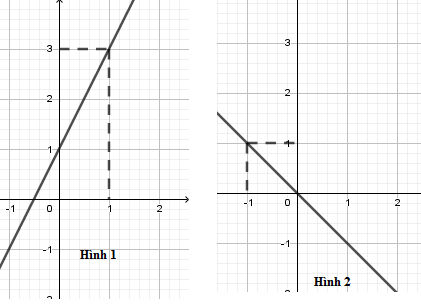
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$
-
A.
Hình 4
-
B.
Hình 2
-
C.
Hình 3
-
D.
Hình 1
Cho hệ phương trình \(\left\{ \begin{array}{l}8x + 7y = 16\\8x - 3y = - 24\end{array} \right.\) . Nghiệm của hệ phương trình là
-
A.
$\left( {x;y} \right) = \left( { - \dfrac{3}{2};4} \right)$
-
B.
$\left( {x;y} \right) = \left( {4; - \dfrac{3}{2}} \right)$
-
C.
$\left( {x;y} \right) = \left( { - \dfrac{3}{2}; - 4} \right)$
-
D.
$\left( {x;y} \right) = \left( { - 2;2} \right)$
Phép tính $\sqrt {{{\left( { - 5} \right)}^2}{{.7}^2}} $ có kết quả là?
-
A.
$35$
-
B.
$5$
-
C.
$ - 35$
-
D.
Không tồn tại.
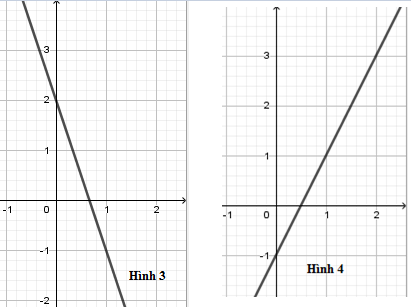
Hình nào dưới đây biểu diễn góc nội tiếp?
-
A.
Hình \(1\)
-
B.
Hình \(2\)
-
C.
Hình $3$
-
D.
Hình \(4\)
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
Với điều kiện nào của \(x\) thì biểu thức \(\dfrac{{\sqrt { - 3x} }}{{{x^2} - 1}}\) có nghĩa?
-
A.
\(x \ne \pm 1\)
-
B.
\(\left\{ \begin{array}{l}x \ge 0\\x \ne - 1\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x \le 0\\x \ne 1\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x \le 0\\x \ne - 1\end{array} \right.\)
Điểm nào sau đây thuộc ĐTHS $y = 2{\rm{x}} + 1$:
-
A.
$(0;1)$
-
B.
$(0; - 1)$
-
C.
$(1;0)$
-
D.
$( - 1;2)$
Cho phương trình: \({x^4} + m{x^2} + 2m + 3 = 0\) (1). Với giá trị nào dưới đây của $m$ thì phương trình (1) có $4$ nghiệm phân biệt ?
-
A.
\(m = - \dfrac{7}{5}\)
-
B.
\(m = - 1\)
-
C.
\(m = - \dfrac{3}{2}\)
-
D.
\(m = 4 - 2\sqrt 7 \)
Một hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh. Tính chiều cao hình trụ biết bán kính hình trụ là $1cm.$
-
A.
\(10\,cm\)
-
B.
$1\,cm$
-
C.
\(2\,cm\)
-
D.
\(0,5\,cm\)
Cho phương trình: \({x^2} + 2\left( {m - 3} \right)x + {m^2} + m + 1 = 0\) (1)
Khẳng định nào trong các khẳng định sau đúng:
-
A.
Với \(m = 3\) phương trình (1) có $2$ nghiệm phân biệt.
-
B.
Với \(m = - 1\) phương trình (1) có nghiệm duy nhất.
-
C.
Với \(m = 2\) phương trình (1) vô nghiệm.
-
D.
Với \(m = 2\) phương trình (1) có $2$ nghiệm phân biệt.
Cho \(B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}\) và \(C = \left( {2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} } \right):\sqrt 3 \). Chọn đáp án đúng.
-
A.
\(B > C\)
-
B.
\(B < C\)
-
C.
\(B = C\)
-
D.
\(B = - C\)
Tính $\Delta '$ và tìm số nghiệm của phương trình \(7{x^2} - 12x + 4 = 0\) .
-
A.
$\Delta ' = 6$ và phương trình có hai nghiệm phân biệt
-
B.
$\Delta ' = 8$ và phương trình có hai nghiệm phân biệt
-
C.
$\Delta ' = 8$ và phương trình có nghiệm kép
-
D.
$\Delta ' = 0$ và phương trình có hai nghiệm phân biệt
Tâm đường tròn nội tiếp của tam giác là
-
A.
giao của ba đường phân giác góc trong tam giác
-
B.
giao ba đường trung trực của tam giác
-
C.
trọng tâm tam giác
-
D.
trực tâm tam giác
Cho $a$ là số không âm, $b$ là số dương. Khẳng định nào sau đây là đúng?
-
A.
$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{b}$
-
B.
$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$
-
C.
$\sqrt {\dfrac{a}{b}}=\dfrac{{ - \sqrt a }}{{\sqrt b }}$
-
D.
$\sqrt {\dfrac{a}{b}}=\dfrac{a}{{\sqrt b }}$
Cho đường tròn $\left( {O;3cm} \right)$, lấy điểm $A$ sao cho $OA = 6cm$. Từ \(A\) vẽ tiếp tuyến $AB,AC$ đến đường tròn $\left( O \right)$ ($B,C$ là tiếp điểm). Chu vi tam giác $ABC$ là
-
A.
$9cm$
-
B.
$9\sqrt 3 cm$
-
C.
$9\sqrt 2 cm$
-
D.
Kết quả khác
Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:
-
A.
$2$
-
B.
$1$
-
C.
$0$
-
D.
$3$
Cho phương trình bậc hai: \({x^2} - 2px + 5 = 0\) có $1$ nghiệm \({x_1} = 2\)
Tìm giá trị của $p$ và nghiệm \({x_2}\) còn lại:
-
A.
\(p = 2;{x_2} = 1\)
-
B.
\(p = \dfrac{5}{2};{x_2} = \dfrac{9}{4}\)
-
C.
\(p = \dfrac{9}{4};{x_2} = \dfrac{5}{2}\)
-
D.
\(p = \dfrac{9}{4};{x_2} = \dfrac{1}{2}\)
Nghiệm của phương trình \(\sqrt {4x - 20} + \sqrt {x - 5} - \dfrac{1}{3}\sqrt {9x - 45} = 4\) là
-
A.
$x = - 9$
-
B.
$x = 5$
-
C.
$x = 8$
-
D.
$x = 9$
Cho biểu thức $P = \left( {\dfrac{{\sqrt x + 1}}{{x - 9}} - \dfrac{1}{{\sqrt x + 3}}} \right)\left( {\sqrt x - 3} \right)$. Rút gọn \(P\) .
-
A.
\(P = \dfrac{4}{{\sqrt x - 3}}\)
-
B.
\(P = \dfrac{4}{{\sqrt x + 3}}\)
-
C.
\(P = \dfrac{2}{{\sqrt x + 3}}\)
-
D.
\(P = \dfrac{1}{{\sqrt x + 3}}\)
Rút gọn biểu thức: $A = \left( {\dfrac{{\sqrt x }}{2} - \dfrac{1}{{2\sqrt x }}} \right)\left( {\dfrac{{x - \sqrt x }}{{\sqrt x + 1}} - \dfrac{{x + \sqrt x }}{{\sqrt x - 1}}} \right)$ v ới \(x > 0;\,\,x \ne 1.\)
-
A.
\(A = - 2\sqrt x \)
-
B.
\(A = 2\sqrt x \)
-
C.
\(A = - \sqrt x \)
-
D.
\(A = 4\sqrt x \)
Với giá trị nào của m thì đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung?
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = - 1$
-
D.
$m = 2$
Cho đường thẳng $d$ vuông góc với $d':y = - \dfrac{1}{3}{\rm{x}}$ và $d$ đi qua $P\left( {1; - 1} \right)$ . Khi đó phương trình đường thẳng $d$ là:
-
A.
$y = 3x - 4$
-
B.
$y = 3x + 4$
-
C.
$y = 3x - 2$
-
D.
$y=3x+1$
Cho hệ phương trình $\left\{ \begin{array}{l}4\sqrt x - 3\sqrt y = 4\\2\sqrt x + \sqrt y = 2\end{array} \right.$ . Biết nghiệm của hệ phương trình là $\left( {x;y} \right)$ , tính $x.y$
-
A.
$2$
-
B.
$0$
-
C.
$-2$
-
D.
$1$
Tìm các giá trị của m để nghiệm của hệ phương trình :
\(\left\{ \begin{array}{l}\dfrac{{2x + 1}}{3} - \dfrac{{y + 1}}{4} = \dfrac{{4x - 2y + 2}}{5}\\\dfrac{{2x - 3}}{4} - \dfrac{{y - 4}}{3} = - 2x + 2y - 2\end{array} \right.\)
cũng là nghiệm của phương trình \(6mx - 5y = 2m - 66\).
-
A.
$m = - 1$
-
B.
$m = 1$
-
C.
$m = 2$
-
D.
$m = 3$
Cho hệ phương trình\(\left\{ \begin{array}{l}mx - y = 2m\\4x - my = m + 6\end{array} \right..\) Trong trường hợp hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right)\), tìm giá trị của m để : \(6x - 2y = 13.\)
-
A.
$m = - 9$
-
B.
$m = 9$
-
C.
$m = 8$
-
D.
$m = - 8$
Hai người đi xe đạp xuất phát đồng thời từ hai thành phố cách nhau \(38\,km\) . Họ đi ngược chiều và gặp nhau sau $2$ giờ. Hỏi vận tốc của người thứ nhất, biết rằng đến khi gặp nhau, người thứ nhất đi được nhiều hơn người thứ hai \(2\,km\) ?
-
A.
$7\,{\rm{km/h}}$
-
B.
$8\,{\rm{km/h}}$
-
C.
$9\,{\rm{km/h}}$
-
D.
$10\,{\rm{km/h}}$
Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt
-
A.
$m = 2$
-
B.
$m = - 2$
-
C.
$m = 4$
-
D.
$m \in \mathbb{R}$
Tìm tham số $m$ để đường thẳng $d:y = 2x + m$ và parabol $\left( P \right):y = 2{x^2}$ không có điểm chung
-
A.
$m < - \dfrac{1}{2}$
-
B.
$m \le - \dfrac{1}{2}$
-
C.
$m > \dfrac{1}{2}$
-
D.
$m \ge \dfrac{1}{2}$
Tìm các giá trị của m để đường thẳng \(d:\,\,y = 2\left( {m - 1} \right)x - m - 1\) cắt parabol (P): \(y = {x^2}\) tại hai điểm có hoành độ trái dấu.
-
A.
$m > - 1$
-
B.
$m < - 1$
-
C.
$m = 1$
-
D.
$m \ne - 1$
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
-
A.
$2$
-
B.
$3$
-
C.
$1$
-
D.
$4$
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
-
A.
$BC = 10$
-
B.
$BC = 11$
-
C.
$BC = 9$
-
D.
$BC = 12$
Một máy bay đang bay ở độ cao $10km$ so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là ${15^0}$ thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? ( làm tròn kết quả đến hai chữ số phần thập phân)
-
A.
$37,32\,km$
-
B.
$373,2\,km$
-
C.
$38,32\,km$
-
D.
$37,52\,km$
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai ?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
-
A.
\(A{B^2}\)
-
B.
\(B{C^2}\)
-
C.
\(A{C^2}\)
-
D.
\(A{M^2}\)
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA, MB\) với \(\left( O \right)\) tại \(A\) và \(B.\) Qua \(A\) vẽ đường thẳng song song với \(MB\) cắt đường tròn tại \(C.\)
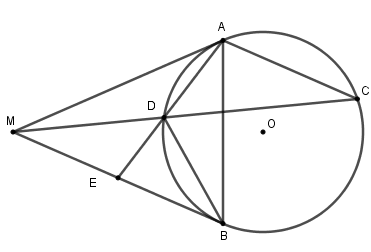
Nối \(C\) với \(M\) cắt đường tròn \(\left( O \right)\) tại \(D.\) Nối \(A\) với \(D\) cắt \(MB\) tại \(E.\) Chọn câu đúng
-
A.
\(ME = 2EB\)
-
B.
\(2ME = EB\)
-
C.
\(ME = EB.\)
-
D.
\(3ME = 2EB\)
Cho \(A\) là điểm cố định trên đường tròn \(\left( {O;R} \right).\) Gọi \(AB\) và \(AC\) là hai dây cung thay đổi trên đường tròn \(\left( O \right)\) thỏa mãn \(\sqrt {AB.AC} = R\sqrt 3 .\) Khi đó vị trí của \(B,\,C\) trên \(\left( O \right)\) để diện tích \(\Delta ABC\) lớn nhất là:
-
A.
\(\Delta ABC\) cân
-
B.
\(\Delta ABC\) đều.
-
C.
\(\Delta ABC\) vuông cân
-
D.
\(\Delta ABC\) vuông
Cho đường thẳng $d:y = x + 2;d':y = - 2x + 5$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $B$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành. Khi đó diện tích tam giác $AMB$ là:
-
A.
$\dfrac{{27}}{6}$ ( đvdt)
-
B.
$27$( đvdt)
-
C.
$\dfrac{{27}}{2}$ (đvdt)
-
D.
$\dfrac{{27}}{4}$(đvdt)
Với \(x;\,\,y;\,\,z\) là các số thực thỏa mãn \(x + y + z + xy + yz + zx = 6\). Tìm giá trị nhỏ nhất của biểu thức:
\(P = \sqrt {4 + {x^4}} + \sqrt {4 + {y^4}} + \sqrt {4 + {z^4}} \).
-
A.
\({{\rm P}_{\min }} = \sqrt 5 \)
-
B.
\({{\rm P}_{\min }} = 3\sqrt 5 \)
-
C.
\({{\rm P}_{\min }} = 5\sqrt 3 \)
-
D.
\({{\rm P}_{\min }} = 3\)
Cho phương trình: \({x^2} - 2mx + 2m - 1 = 0\) .
Tìm $m$ để phương trình có $2$ nghiệm phân biệt thỏa mãn: \(2\left( {x_1^2 + x_2^2} \right) - 5{x_1}{x_2} = - 1\).
-
A.
\(m = 1\)
-
B.
\(m = \dfrac{5}{4}\)
-
C.
\(m = - 4\)
-
D.
\(m = \dfrac{{ - 7}}{4}\)
Lời giải và đáp án
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$


-
A.
Hình 4
-
B.
Hình 2
-
C.
Hình 3
-
D.
Hình 1
Đáp án : D
Sử dụng cách vẽ đồ thị hàm số
Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng
Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
Đồ thị hàm số $y = 2x + 1$ là đường thẳng đi qua hai điểm có tọa độ $\left( {0;1} \right)$ và $\left( {1;3} \right)$ nên hình 1 là đồ thị hàm số $y = 2x + 1$.
Cho hệ phương trình \(\left\{ \begin{array}{l}8x + 7y = 16\\8x - 3y = - 24\end{array} \right.\) . Nghiệm của hệ phương trình là
-
A.
$\left( {x;y} \right) = \left( { - \dfrac{3}{2};4} \right)$
-
B.
$\left( {x;y} \right) = \left( {4; - \dfrac{3}{2}} \right)$
-
C.
$\left( {x;y} \right) = \left( { - \dfrac{3}{2}; - 4} \right)$
-
D.
$\left( {x;y} \right) = \left( { - 2;2} \right)$
Đáp án : A
Ta có \(\left\{ \begin{array}{l}8x + 7y = 16\\8x - 3y = - 24\end{array} \right.\)$ \Leftrightarrow \left\{ \begin{array}{l}8x + 7y = 16\\8x + 7y - \left( {8x - 3y} \right) = 16 - \left( { - 24} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8x + 7y = 16\\10y = 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 4\\8x + 7.4 = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 4\\x = - \dfrac{3}{2}\end{array} \right.$
Vậy hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( { - \dfrac{3}{2};4} \right)$
Phép tính $\sqrt {{{\left( { - 5} \right)}^2}{{.7}^2}} $ có kết quả là?
-
A.
$35$
-
B.
$5$
-
C.
$ - 35$
-
D.
Không tồn tại.
Đáp án : A
-Sử dụng công thức khai phương một tích: Với hai số $a,b$ không âm, ta có $\sqrt a .\sqrt b = \sqrt {ab} $
-Sử dụng hằng đẳng thức $\sqrt {{A^2}} = \left| A \right|$
Cách giải:
$\sqrt {{{\left( { - 5} \right)}^2}{{.7}^2}} = \sqrt {{{\left( { - 5} \right)}^2}} .\sqrt {{7^2}} = \left| { - 5} \right|.\left| 7 \right| = 5.7 = 35$.
Hình nào dưới đây biểu diễn góc nội tiếp?

-
A.
Hình \(1\)
-
B.
Hình \(2\)
-
C.
Hình $3$
-
D.
Hình \(4\)
Đáp án : B
Sử dụng định nghĩa góc nội tiếp:
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Hình \(1\) góc \(\widehat {BOA}\) là góc ở tâm .
Hình \(3\) có \(1\) cạnh không phải là dây của đường tròn.
Hình \(4\) đỉnh $B$ không nằm trên đường tròn.
Hình \(2\) góc \(\widehat {BCA}\) là góc nội tiếp chắn cung \(AB\)
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
Đáp án : B
Từ tỉ số lượng giác sin, cos để chứng minh.
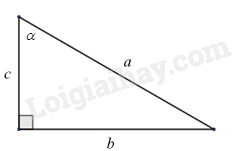
Giả sử ta có tam giác vuông có các cạnh và góc $\alpha $ như hình vẽ.
Áp dụng tỉ số lượng giác của góc nhọn, ta có:
$\sin \alpha =\frac{b}{a},\cos \alpha =\frac{c}{a},\tan \alpha =\frac{b}{c},\cot \alpha =\frac{c}{b}$.
Ta có: ${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha ={{\left( \frac{b}{a} \right)}^{2}}+{{\left( \frac{c}{a} \right)}^{2}}=\frac{{{b}^{2}}+{{c}^{2}}}{{{a}^{2}}}=\frac{{{a}^{2}}}{{{a}^{2}}}=1$
Vậy ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
Với điều kiện nào của \(x\) thì biểu thức \(\dfrac{{\sqrt { - 3x} }}{{{x^2} - 1}}\) có nghĩa?
-
A.
\(x \ne \pm 1\)
-
B.
\(\left\{ \begin{array}{l}x \ge 0\\x \ne - 1\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x \le 0\\x \ne 1\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x \le 0\\x \ne - 1\end{array} \right.\)
Đáp án : D
+ \(\sqrt A \) có nghĩa khi \(A \ge 0\)
+ \(\dfrac{A}{B}\) có nghĩa khi \(B \ne 0.\)
Ta có \(\dfrac{{\sqrt { - 3x} }}{{{x^2} - 1}}\) có nghĩa khi \( \Leftrightarrow \left\{ \begin{array}{l} - 3x \ge 0\\{x^2} - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\{x^2} \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\x \ne 1\\x \ne - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\x \ne - 1\end{array} \right.\)
Điểm nào sau đây thuộc ĐTHS $y = 2{\rm{x}} + 1$:
-
A.
$(0;1)$
-
B.
$(0; - 1)$
-
C.
$(1;0)$
-
D.
$( - 1;2)$
Đáp án : A
Sử dụng kiến thức: Điểm $({x_0};{y_0})$ thuộc ĐTHS $y = {\rm{ax}} + b \Leftrightarrow {\rm{a}}{{\rm{x}}_0} + b = {y_0}$.
Đáp án A: Thay $ x_0=0;y_0=1$ vào hàm số, ta có $ 2.0 + 1 = 1 \Rightarrow (0;1)$ thuộc ĐTHS đã cho.
Cho phương trình: \({x^4} + m{x^2} + 2m + 3 = 0\) (1). Với giá trị nào dưới đây của $m$ thì phương trình (1) có $4$ nghiệm phân biệt ?
-
A.
\(m = - \dfrac{7}{5}\)
-
B.
\(m = - 1\)
-
C.
\(m = - \dfrac{3}{2}\)
-
D.
\(m = 4 - 2\sqrt 7 \)
Đáp án : A
Đặt \({x^2} = t\) $( t \ge 0)$ đưa phương trình (1) thành phương trình bậc $2$ với ẩn $t$ và tham số $m$.
Phương trình mới thu được: \({t^2} + mt + 2m + 3 = 0\) (2)
Để phương trình (1) có $4$ nghiệm phân biệt, thì phương trình (2) có $2$ nghiệm dương phân biệt.
Biện luận phương trình (2) theo tham số $m$ để có $2$ nghiệm dương phân biệt.
Đặt: \({x^2} = t\left( {t \ge 0} \right)\) ta được: \({t^2} + mt + 2m + 3 = 0\) (2).
Để phương trình (1) có $4$ nghiệm phân biệt thì phương trình (2) có $2$ nghiệm dương phân biệt
Phương trình (2) có $2$ nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right.\)
\(\left\{ \begin{array}{l}{m^2} - 4\left( {2m + 3} \right) > 0\\ - m > 0\\2m + 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 8m - 12 > 0\\m < 0\\m > - \dfrac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 4 + 2\sqrt 7 \\m < 4 - 2\sqrt 7 \end{array} \right.\\ - \dfrac{3}{2} < m < 0\end{array} \right. \Leftrightarrow - \dfrac{3}{2} < m < 4 - 2\sqrt 7 \)
Với các giá trị thuộc \( - \dfrac{3}{2} < m < 4 - 2\sqrt 7 \) thì phương trình đã cho có $4$ nghiệm phân biệt.
Nhận thấy trong các đáp án thì thì chỉ có \(m = - \dfrac{7}{5}\) thỏa mãn \( - \dfrac{3}{2} < m < 4 - 2\sqrt 7 \) để phương trình đã cho có $4$ nghiệm phân biệt.
Một hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh. Tính chiều cao hình trụ biết bán kính hình trụ là $1cm.$
-
A.
\(10\,cm\)
-
B.
$1\,cm$
-
C.
\(2\,cm\)
-
D.
\(0,5\,cm\)
Đáp án : B
Sử dụng công thức tính diện tích xung quanh, diện tích toàn phần của hình trụ có bán kính đáy $R$ và chiều cao \(h\) là \({S_{xq}} = 2\pi {R}h\) ; \({S_{tp}} = 2\pi {R}h + 2\pi {R^2}\)
Gọi chiều cao của hình trụ là \(h.\)
Ta có \({S_{xq}} = 2\pi {R}h\) ; \({S_{tp}} = 2\pi {R}h + 2\pi {R^2}\) mà theo giả thiết thì \({S_{tp}} = 2{S_{xq}}\) nên ta có
\(2\pi {R}h + 2\pi {R^2} = 2.2\pi {R}h \Leftrightarrow 2\pi {R^2} = 2\pi {R}h \)\(\Rightarrow h = R=1cm.\)
Cho phương trình: \({x^2} + 2\left( {m - 3} \right)x + {m^2} + m + 1 = 0\) (1)
Khẳng định nào trong các khẳng định sau đúng:
-
A.
Với \(m = 3\) phương trình (1) có $2$ nghiệm phân biệt.
-
B.
Với \(m = - 1\) phương trình (1) có nghiệm duy nhất.
-
C.
Với \(m = 2\) phương trình (1) vô nghiệm.
-
D.
Với \(m = 2\) phương trình (1) có $2$ nghiệm phân biệt.
Đáp án : C
Phương trình đã cho là phương trình bậc $2$ ẩn $x$ và tham số m.
Để xem phương trình có nghiệm hay không, ta xét đại lượng \(\Delta \) của phương trình.
Thay các giá trị của $m$ vào để tìm đáp án đúng.
Phương trình (1) là phương trình bậc hai với ẩn $x$ và tham số $m$.
Xét: \(\Delta ' = {\left( {m - 3} \right)^2} - \left( {{m^2} + m + 1} \right) = {m^2} - 6m + 9 - {m^2} - m - 1 = - 7m + 8\).
\( \bullet \) Phương trình đã cho vô nghiệm \( \Leftrightarrow \Delta ' < 0 \Leftrightarrow - 7m + 8 < 0 \Leftrightarrow m > \dfrac{8}{7}\).
\( \bullet \) Phương trình đã cho có nghiệm duy nhất \( \Leftrightarrow \Delta ' = 0 \Leftrightarrow - 7m + 8 = 0 \Leftrightarrow m = \dfrac{8}{7}\).
\( \bullet \) Phương trình đã cho có $2$ nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0 \Leftrightarrow - 7m + 8 > 0 \Leftrightarrow m < \dfrac{8}{7}\).
Như vậy
+ Với $m=3>\dfrac{8}{7}$ thì phương trình vô nghiệm nên A sai.
+ Với $m=-1<\dfrac{8}{7}$ thì phương trình có hai nghiệm phân biệt nên B sai.
+ Với $ m=2>\dfrac{8}{7}$ thì phương trình vô nghiệm nên C đúng, D sai.
Vậy đáp án đúng là đáp án C.
Cho \(B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}\) và \(C = \left( {2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} } \right):\sqrt 3 \). Chọn đáp án đúng.
-
A.
\(B > C\)
-
B.
\(B < C\)
-
C.
\(B = C\)
-
D.
\(B = - C\)
Đáp án : A
+ Tính \(B;C\) bằng cách sử dụng các công thức
Với \(A > 0\) và \(A \ne {B^2}\) thì \(\dfrac{C}{{\sqrt A \pm B}} = \dfrac{{C(\sqrt A \mp B)}}{{A - {B^2}}}\)
Khai phương một tích: \(\sqrt {A.B} = \sqrt A .\sqrt B {\rm{ }}(A \ge 0,B \ge 0)\)
+ So sánh \(B;C.\)
Ta có \(B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}\)
\( = \dfrac{{2\sqrt 2 }}{{\sqrt 2 .\sqrt 2 }} + \dfrac{{\sqrt 3 + \sqrt 2 }}{{\left( {\sqrt 3 - \sqrt 2 } \right)\left( {\sqrt 3 + \sqrt 2 } \right)}} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}\)
$ = \dfrac{{2\sqrt 2 }}{2} + \dfrac{{\sqrt 3 + \sqrt 2 }}{{3 - 2}} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{3 - 1}}$ $= \sqrt 2 + \dfrac{{\sqrt 3 + \sqrt 2 }}{1} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{2}$
\( = \sqrt 2 + \sqrt 3 + \sqrt 2 - \left( {\sqrt 3 + 1} \right)\)
\( = \sqrt 2 + \sqrt 3 + \sqrt 2 - \sqrt 3 - 1\)
\( = 2\sqrt 2 - 1\)
Lại có
$\begin{array}{l}C = (2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} ):\sqrt 3 \\ = \left( {2\sqrt 3 - 5\sqrt {9.3} + 4\sqrt {4.3} } \right):\sqrt 3 \\= (2\sqrt 3 - 5.3\sqrt 3 + 4.2\sqrt 3 ):\sqrt 3 \\ = - 5\sqrt 3 :\sqrt 3 \\ = - 5\end{array}$
Nhận thấy \(B = 2\sqrt 2 - 1 > 0;\,C = - 5 < 0 \Rightarrow B > C\)
Tính $\Delta '$ và tìm số nghiệm của phương trình \(7{x^2} - 12x + 4 = 0\) .
-
A.
$\Delta ' = 6$ và phương trình có hai nghiệm phân biệt
-
B.
$\Delta ' = 8$ và phương trình có hai nghiệm phân biệt
-
C.
$\Delta ' = 8$ và phương trình có nghiệm kép
-
D.
$\Delta ' = 0$ và phương trình có hai nghiệm phân biệt
Đáp án : B
Xét phương trình bậc hai một ẩn $a{{x}^{2}}+bx+c=0\left( a\ne 0 \right)$, với $b=2b'$ và $\Delta '=b{{'}^{2}}-ac$.
- Nếu $\Delta '>0$ thì phương trình có hai nghiệm phân biệt:
${{x}_{1}}=\frac{-b'+\sqrt{\Delta '}}{a};{{x}_{2}}=\frac{-b'-\sqrt{\Delta '}}{a}$.
- Nếu $\Delta '=0$ thì phương trình có nghiệm kép ${{x}_{1}}={{x}_{2}}=-\frac{b'}{a}$.
- Nếu $\Delta '<0$ thì phương trình vô nghiệm.
Phương trình \(7{x^2} - 12x + 4 = 0\) có $a = 7;b' = - 6;c = 4$ suy ra
$\Delta ' = {\left( {b'} \right)^2} - ac = {\left( { - 6} \right)^2} - 4.7 = 8 > 0$
Nên phương trình có hai nghiệm phân biệt.
Tâm đường tròn nội tiếp của tam giác là
-
A.
giao của ba đường phân giác góc trong tam giác
-
B.
giao ba đường trung trực của tam giác
-
C.
trọng tâm tam giác
-
D.
trực tâm tam giác
Đáp án : A
Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác các góc trong tam giác.
Cho $a$ là số không âm, $b$ là số dương. Khẳng định nào sau đây là đúng?
-
A.
$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{b}$
-
B.
$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$
-
C.
$\sqrt {\dfrac{a}{b}}=\dfrac{{ - \sqrt a }}{{\sqrt b }}$
-
D.
$\sqrt {\dfrac{a}{b}}=\dfrac{a}{{\sqrt b }}$
Đáp án : B
Sử dụng kiến thức căn thức bậc hai của một thương.
Với số $a$ không âm và số $b$ dương , ta có $\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$.
Cho đường tròn $\left( {O;3cm} \right)$, lấy điểm $A$ sao cho $OA = 6cm$. Từ \(A\) vẽ tiếp tuyến $AB,AC$ đến đường tròn $\left( O \right)$ ($B,C$ là tiếp điểm). Chu vi tam giác $ABC$ là
-
A.
$9cm$
-
B.
$9\sqrt 3 cm$
-
C.
$9\sqrt 2 cm$
-
D.
Kết quả khác
Đáp án : B
Dựa vào tính chất tiếp tuyến của đường tròn
Định lí Pi-ta-go
Hệ thức lượng trong tam giác vuông
Cách tính chu vi hình tam giác
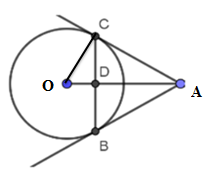
Gọi $D$ là giao điểm của $BC$ và $OA$
Có $OC \bot AC$ (tính chất tiếp tuyến của đường tròn)
Xét $\Delta OAC$ vuông tại \(C\), ta có: $O{C^2} + C{A^2} = O{A^2}$ (Py-ta-go)
\( \Rightarrow A{C^2} = {\rm{ }}O{A^2} - {\rm{ }}O{C^2} = {6^2} - {3^2} = 36 - 9 = 27 \Rightarrow AC = 3\sqrt 3 cm\)
Mà $AC=AB$ (tính chất hai tiếp tuyến cắt nhau) nên $AB = 3\sqrt 3 cm$.
Vì $AC=AB;OB=OC$ nên $OA$ là đường trung trực của $BC$ hay $OA \bot BC$ tại $D$ và $D$ là trung điểm của $CB.$
Xét tam giác vuông $OCA$ có $CD$ là đường cao nên:
\(CD = \dfrac{{OC.CA}}{{OA}} = \dfrac{{3.3\sqrt 3 }}{6} = \dfrac{{3\sqrt 3 }}{2} \Rightarrow BC = 2CD = 3\sqrt 3 cm\)
Vậy chu vi tam giác $ABC$ là $3\sqrt 3 + 3\sqrt 3 + 3\sqrt 3 = 9\sqrt 3 cm$
Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:
-
A.
$2$
-
B.
$1$
-
C.
$0$
-
D.
$3$
Đáp án : A
Bước 1: Giải phương trình hoành độ giao điểm.
Bước 2: Số nghiệm vừa tìm được của phương trình là số giao điểm của đường thẳng và parabol
Xét phương trình hoành độ giao điểm ${x^2} = 2x + 4 \Leftrightarrow {x^2} - 2x - 4 = 0$ có $\Delta ' = 5 > 0$ nên phương trình có hai nghiệm phân biệt hay đường thẳng cắt parabol tại hai điểm phân biệt.
Cho phương trình bậc hai: \({x^2} - 2px + 5 = 0\) có $1$ nghiệm \({x_1} = 2\)
Tìm giá trị của $p$ và nghiệm \({x_2}\) còn lại:
-
A.
\(p = 2;{x_2} = 1\)
-
B.
\(p = \dfrac{5}{2};{x_2} = \dfrac{9}{4}\)
-
C.
\(p = \dfrac{9}{4};{x_2} = \dfrac{5}{2}\)
-
D.
\(p = \dfrac{9}{4};{x_2} = \dfrac{1}{2}\)
Đáp án : C
Thay nghiệm \({x_1} = 2\) vào phương trình đã cho để tìm $p$.
Thay giá trị $p$ tìm được vào phương trình, phân tích thành phương trình tích với nhân tử là \((x - 2)\) để tìm nghiệm còn lại.
Thay \(x = 2\) vào phương trình đã cho ta được: \(4 - 4p + 5 = 0 \Leftrightarrow 4p = 9 \Leftrightarrow p = \dfrac{9}{4}\).
Thay \(p = \dfrac{9}{4}\) vào phương trình đã cho ta được: \({x^2} - \dfrac{9}{2}x + 5 = 0 \Leftrightarrow 2{x^2} - 9x + 10 = 0 \Leftrightarrow (x - 2)(2x - 5) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \dfrac{5}{2}\end{array} \right.\)
Vậy nghiệm còn lại là \({x_2} = \dfrac{5}{2}\).
Nghiệm của phương trình \(\sqrt {4x - 20} + \sqrt {x - 5} - \dfrac{1}{3}\sqrt {9x - 45} = 4\) là
-
A.
$x = - 9$
-
B.
$x = 5$
-
C.
$x = 8$
-
D.
$x = 9$
Đáp án : D
-Tìm điều kiện xác định
-Sử dụng công thức khai phương một tích: Với hai số $a,b$ không âm, ta có $\sqrt {ab} = \sqrt a .\sqrt b $
và nhóm nhân tử chung để đưa phương trình về dạng đã biết.
-So sánh điều kiện rồi kết luận nghiệm.
Điều kiện: $\left\{ \begin{array}{l}4x - 20 \ge 0\\x - 5 \ge 0\\9x - 45 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 5 \ge 0\\4\left( {x - 5} \right) \ge 0\\9\left( {x - 5} \right) \ge 0\end{array} \right. \Leftrightarrow x - 5 \ge 0 \Leftrightarrow x \ge 5$
Với điều kiện trên ta có \(\sqrt {4x - 20} + \sqrt {x - 5} - \dfrac{1}{3}\sqrt {9x - 45} = 4.\)$ \Leftrightarrow \sqrt {4\left( {x - 5} \right)} + \sqrt {x - 5} - \dfrac{1}{3}\sqrt {9\left( {x - 5} \right)} = 4$
$ \Leftrightarrow \sqrt 4 .\sqrt {x - 5} + \sqrt {x - 5} - \dfrac{1}{3}\sqrt 9 \sqrt {x - 5} = 4 \Leftrightarrow 2\sqrt {x - 5} + \sqrt {x - 5} - \dfrac{1}{3}.3.\sqrt {x - 5} = 4 \Leftrightarrow 2\sqrt {x - 5} = 4 \Leftrightarrow \sqrt {x - 5} = 2$
$ \Leftrightarrow x - 5 = {2^2} \Leftrightarrow x - 5 = 4 \Leftrightarrow x = 9\,\left( {TM} \right)$
Vậy nghiệm của phương trình là $x = 9$.
Cho biểu thức $P = \left( {\dfrac{{\sqrt x + 1}}{{x - 9}} - \dfrac{1}{{\sqrt x + 3}}} \right)\left( {\sqrt x - 3} \right)$. Rút gọn \(P\) .
-
A.
\(P = \dfrac{4}{{\sqrt x - 3}}\)
-
B.
\(P = \dfrac{4}{{\sqrt x + 3}}\)
-
C.
\(P = \dfrac{2}{{\sqrt x + 3}}\)
-
D.
\(P = \dfrac{1}{{\sqrt x + 3}}\)
Đáp án : B
+ Phân tích mẫu thức thành nhân tử rồi qui đồng mẫu các phân thức
+ Từ đó rút gọn phân thức
Điều kiện \(x \ge 0;x \ne 9.\)
P = $\left[ {\dfrac{{\sqrt x + 1}}{{(\sqrt x + 3)(\sqrt x - 3)}} - \dfrac{{\sqrt x - 3}}{{(\sqrt x + 3)(\sqrt x - 3)}}} \right]$$\left( {\sqrt x - 3} \right)$
= $\dfrac{{\sqrt x + 1 - (\sqrt x - 3)}}{{(\sqrt x + 3)(\sqrt x - 3)}}$$\left( {\sqrt x - 3} \right)$
= $\dfrac{{\sqrt x + 1 - \sqrt x + 3}}{{(\sqrt x + 3)(\sqrt x - 3)}}$$\left( {\sqrt x - 3} \right)$
= $\dfrac{4}{{\sqrt x + 3}}$
Vậy \(P = \dfrac{4}{{\sqrt x + 3}}\) với \(x \ge 0;x \ne 9.\)
Rút gọn biểu thức: $A = \left( {\dfrac{{\sqrt x }}{2} - \dfrac{1}{{2\sqrt x }}} \right)\left( {\dfrac{{x - \sqrt x }}{{\sqrt x + 1}} - \dfrac{{x + \sqrt x }}{{\sqrt x - 1}}} \right)$ v ới \(x > 0;\,\,x \ne 1.\)
-
A.
\(A = - 2\sqrt x \)
-
B.
\(A = 2\sqrt x \)
-
C.
\(A = - \sqrt x \)
-
D.
\(A = 4\sqrt x \)
Đáp án : A
+ Phân tích mẫu thức thành nhân tử rồi qui đồng mẫu các phân thức
+ Từ đó rút gọn phân thức
$\begin{array}{l}A = \left( {\dfrac{{\sqrt x }}{2} - \dfrac{1}{{2\sqrt x }}} \right)\left( {\dfrac{{x - \sqrt x }}{{\sqrt x + 1}} - \dfrac{{x + \sqrt x }}{{\sqrt x - 1}}} \right) = \dfrac{{x - 1}}{{2\sqrt x }}.\left( {\dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x + 1}} - \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x - 1}}} \right)\\\,\,\,\,\,\, = \dfrac{{x - 1}}{{2\sqrt x }}.\dfrac{{\sqrt x {{\left( {\sqrt x - 1} \right)}^2} - \sqrt x {{\left( {\sqrt x + 1} \right)}^2}}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \dfrac{{x - 1}}{{2\sqrt x }}.\dfrac{{\sqrt x \left[ {x - 2\sqrt x + 1 - \left( {x + 2\sqrt x + 1} \right)} \right]}}{{x - 1}}\\\,\,\,\,\,\, = \dfrac{{x - 2\sqrt x + 1 - x - 2\sqrt x - 1}}{2} = \dfrac{{ - 4\sqrt x }}{2} = - 2\sqrt x .\end{array}$
Vậy \(A = - 2\sqrt x \) với \(x > 0;\,\,x \ne 1.\)
Với giá trị nào của m thì đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung?
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = - 1$
-
D.
$m = 2$
Đáp án : A
Để hai đường thẳng ${d_1}:y = ax + b$ và ${d_2}:y = a'x + b'$ cắt nhau tại một điểm trên trục tung thì $\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$
Để hai đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung thì
$\left\{ \begin{array}{l} - 2 \ne 5\\m + 2 = 5 - 2m\end{array} \right.$$ \Leftrightarrow 3m = 3 \Leftrightarrow m = 1$.
Cho đường thẳng $d$ vuông góc với $d':y = - \dfrac{1}{3}{\rm{x}}$ và $d$ đi qua $P\left( {1; - 1} \right)$ . Khi đó phương trình đường thẳng $d$ là:
-
A.
$y = 3x - 4$
-
B.
$y = 3x + 4$
-
C.
$y = 3x - 2$
-
D.
$y=3x+1$
Đáp án : A
Sử dụng kiến thức:
+) $d \bot d' \Leftrightarrow a.a' = - 1$
+) Điểm $({x_0};{y_0})$ thuộc đồ thị hàm số $y = {\rm{ax}} + b $$\Leftrightarrow {\rm{a}}{{\rm{x}}_0} + b = {y_0}$.
Đường thẳng $d$ vuông góc với đường thẳng $d' \Rightarrow a.\dfrac{{ - 1}}{3} = - 1 \Leftrightarrow a = 3$
Đường thẳng $d$ đi qua điểm $P(1;-1) \Rightarrow 3.1 + b = - 1 \Leftrightarrow b = - 4$
$ \Rightarrow d:y = 3x - 4$.
Cho hệ phương trình $\left\{ \begin{array}{l}4\sqrt x - 3\sqrt y = 4\\2\sqrt x + \sqrt y = 2\end{array} \right.$ . Biết nghiệm của hệ phương trình là $\left( {x;y} \right)$ , tính $x.y$
-
A.
$2$
-
B.
$0$
-
C.
$-2$
-
D.
$1$
Đáp án : B
ĐK: $x \ge 0;y \ge 0$
Ta có $\left\{ \begin{array}{l}4\sqrt x - 3\sqrt y = 4\\2\sqrt x + \sqrt y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4\sqrt x - 3\sqrt y = 4\\4\sqrt x + 2\sqrt y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5\sqrt y = 0\\2\sqrt x + \sqrt y = 2\end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}\sqrt y = 0\\2\sqrt x = 2\end{array} \right.$
$\Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = 1\end{array} \right.$ (Thỏa mãn)
Vậy hệ phương trình có 1 nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;0} \right) \Rightarrow x.y = 0.\)
Tìm các giá trị của m để nghiệm của hệ phương trình :
\(\left\{ \begin{array}{l}\dfrac{{2x + 1}}{3} - \dfrac{{y + 1}}{4} = \dfrac{{4x - 2y + 2}}{5}\\\dfrac{{2x - 3}}{4} - \dfrac{{y - 4}}{3} = - 2x + 2y - 2\end{array} \right.\)
cũng là nghiệm của phương trình \(6mx - 5y = 2m - 66\).
-
A.
$m = - 1$
-
B.
$m = 1$
-
C.
$m = 2$
-
D.
$m = 3$
Đáp án : A
Bước 1 : Giải hệ phương trình quy về hệ phương trình bậc nhất hai ẩn
Bước 2 : Thay nghiệm vừa tìm được vào phương trình chưa tham số $m$ để tìm $m$
Ta có \(\left\{ \begin{array}{l}\dfrac{{2x + 1}}{3} - \dfrac{{y + 1}}{4} = \dfrac{{4x - 2y + 2}}{5}\\\dfrac{{2x - 3}}{4} - \dfrac{{y - 4}}{3} = - 2x + 2y - 2\end{array} \right.\)
$ \left\{ \begin{array}{l}40x + 20 - 15y - 15 = 48x - 24y + 24\\6x - 9 - 4y + 16 = - 24x + 24y - 24\end{array} \right.$
$\left\{ \begin{array}{l}8x - 9y = - 19\\30x - 28y = - 31\end{array} \right.$
$ \left\{ \begin{array}{l}120x - 135y = - 285\\120x - 112y = - 124\end{array} \right.$
$ \left\{ \begin{array}{l}x = \dfrac{{11}}{2}\\y = 7\end{array} \right.$
Thay $x = \dfrac{{11}}{2};y = 7$ vào phương trình \(6mx - 5y = 2m - 66\) ta được
$6m.\dfrac{{11}}{2} - 5.7 = 2m - 66$
$\Leftrightarrow 31m = -31$ $\Leftrightarrow m = -1.$
Cho hệ phương trình\(\left\{ \begin{array}{l}mx - y = 2m\\4x - my = m + 6\end{array} \right..\) Trong trường hợp hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right)\), tìm giá trị của m để : \(6x - 2y = 13.\)
-
A.
$m = - 9$
-
B.
$m = 9$
-
C.
$m = 8$
-
D.
$m = - 8$
Đáp án : C
Bước 1: Giải hệ phương trình tìm được nghiệm $\left( {x,y} \right)$ theo tham số $m$
Bước 2: Thay $x,y$ vừa tìm được vào phương trình yêu cầu để tìm $m$
Ta có \(\left\{ \begin{array}{l}mx - y = 2m\\4x - my = m + 6\end{array} \right..\)$ \Leftrightarrow \left\{ \begin{array}{l}y = mx - 2m\\4x - m\left( {mx - 2m} \right) = m + 6\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}y = mx - 2m\\x\left( {{m^2} - 4} \right) = 2{m^2} - m - 6\end{array} \right.$
Hệ phương trình có nghiệm duy nhất khi ${m^2} - 4 \ne 0 \Leftrightarrow m \ne \left\{ { -2;2} \right\}$
Khi đó $x = \dfrac{{2{m^2} - m - 6}}{{{m^2} - 4}} = \dfrac{{\left( {2m + 3} \right)\left( {m - 2} \right)}}{{\left( {m - 2} \right)\left( {m + 2} \right)}} = \dfrac{{2m + 3}}{{m + 2}}$$ \Rightarrow y = m.\dfrac{{2m + 3}}{{m + 2}} - 2m$.
Thay $\left\{ \begin{array}{l}x = \dfrac{{2m + 3}}{{m + 2}}\\y = \dfrac{{ - m}}{{m + 2}}\end{array} \right.$ vào phương trình \(6x - 2y = 13\) ta được
$6.\dfrac{{2m + 3}}{{m + 2}} - 2.\dfrac{{ - m}}{{m + 2}} = 13$
$\Leftrightarrow \dfrac{{14m + 18}}{{m + 2}} = 13$
$\Rightarrow 14m + 18 = 13m + 26 $
$\Leftrightarrow m = 8\left( {TM} \right)$
Vậy $m = 8$ là giá trị cần tìm.
Hai người đi xe đạp xuất phát đồng thời từ hai thành phố cách nhau \(38\,km\) . Họ đi ngược chiều và gặp nhau sau $2$ giờ. Hỏi vận tốc của người thứ nhất, biết rằng đến khi gặp nhau, người thứ nhất đi được nhiều hơn người thứ hai \(2\,km\) ?
-
A.
$7\,{\rm{km/h}}$
-
B.
$8\,{\rm{km/h}}$
-
C.
$9\,{\rm{km/h}}$
-
D.
$10\,{\rm{km/h}}$
Đáp án : D
Gọi vận tốc của người thứ nhất và người thứ hai lần lượt là $x,y\,\,\,\left( {{\rm{km/h}},\,\,x,y > 0} \right)$
Lập hệ phương trình và giải để tìm x.
Gọi vận tốc của người thứ nhất và người thứ hai lần lượt là $x,y\,\,\,\left( {{\rm{km/h}},\,\,x,y > 0} \right)$
Quãng đường người thứ nhất đi được khi gặp nhau là $2x$ $\left( {km} \right)$
Quãng đường người thứ hai đi được đến khi gặp nhau là $2y\,\,\left( {km} \right)$
Ta có hệ phương trình $\left\{ \begin{array}{l}2x + 2y = 38\\2x - 2y = 2\end{array} \right. $
suy ra $\left\{ \begin{array}{l}x = 10\\y = 9\end{array} \right.$ (thỏa mãn)
Vậy vận tốc của người thứ nhất là $10\,\,\left( {{\mathop{\rm km}\nolimits} /h} \right)$.
Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt
-
A.
$m = 2$
-
B.
$m = - 2$
-
C.
$m = 4$
-
D.
$m \in \mathbb{R}$
Đáp án : D
Bước 1: Xét phương trình hoành độ giao điểm của đường thẳng và parabol
Bước 2: Để đường thẳng cắt parabol tại hai điểm phân biệt thì phương trình hoành độ giao điểm có hai nghiệm phân biệt.
Xét phương trình hoành độ giao điểm $\dfrac{{{x^2}}}{2} = mx + 2 \Leftrightarrow {x^2} - 2mx - 4 = 0$ có $\Delta ' = {m^2} + 4$
Vì $\Delta ' = {m^2} + 4 > 0;\forall m$ nên đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt với mọi $m$.
Tìm tham số $m$ để đường thẳng $d:y = 2x + m$ và parabol $\left( P \right):y = 2{x^2}$ không có điểm chung
-
A.
$m < - \dfrac{1}{2}$
-
B.
$m \le - \dfrac{1}{2}$
-
C.
$m > \dfrac{1}{2}$
-
D.
$m \ge \dfrac{1}{2}$
Đáp án : A
Bước 1: Xét phương trình hoành độ giao điểm của đường thẳng và parabol
Bước 2: Để đường thẳng không cắt parabol thì phương trình hoành độ giao điểm vô nghiệm
Xét phương trình hoành độ giao điểm $2{x^2} = 2x + m \Leftrightarrow 2{x^2} - 2x - m = 0$ có $\Delta ' = 1 + 2m$
Để đường thẳng $d:y = 2x + m$ không cắt parabol $\left( P \right):y = 2{x^2}$ thì $\Delta ' < 0 \Leftrightarrow 2m + 1 < 0 \Leftrightarrow m < - \dfrac{1}{2}$
Tìm các giá trị của m để đường thẳng \(d:\,\,y = 2\left( {m - 1} \right)x - m - 1\) cắt parabol (P): \(y = {x^2}\) tại hai điểm có hoành độ trái dấu.
-
A.
$m > - 1$
-
B.
$m < - 1$
-
C.
$m = 1$
-
D.
$m \ne - 1$
Đáp án : B
+ Xét phương trình hoành độ giao điểm.
+ Phương trình bậc hai: \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm trái dấu \( \Leftrightarrow a.c < 0\).
Phương trình hoành độ giao điểm của d và (P) là: \({x^2} - 2\left( {m - 1} \right)x + m + 1 = 0\,\,\left( * \right)\)
Ta có: \(a = 1;\,b = - 2\left( {m - 1} \right);\,c = m + 1\)
Đường thẳng d cắt (P) tại 2 điểm có hoành độ trái dấu \( \Leftrightarrow \left( * \right)\) có 2 nghiệm trái dấu \( \Leftrightarrow ac < 0\)
\( \Leftrightarrow 1.\left( {m + 1} \right) < 0 \Leftrightarrow m < - 1\)
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
-
A.
$2$
-
B.
$3$
-
C.
$1$
-
D.
$4$
Đáp án : B
Sử dụng định nghĩa tỉ số lượng giác của góc nhọn và tam giác đồng dạng.
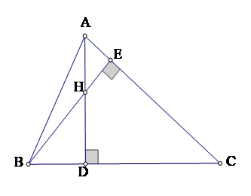
Xét tam giác vuông $ABD$ và $ADC$, ta có: \(\tan B = \dfrac{{AD}}{{BD}};tanC = \dfrac{{AD}}{{CD}}\).
Suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{BD.CD}}\) (1)
Lại có \(\widehat {HBD} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)) và \(\widehat {HDB} = \widehat {ADC} = {90^0}\).
Do đó \(\Delta BDH \backsim \Delta ADC\) (g.g), suy ra \(\dfrac{{DH}}{{DC}} = \dfrac{{BD}}{{AD}}\), do đó \(BD.DC = DH.AD\) (2).
Từ (1) và (2) suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{DH.AD}} = \dfrac{{AD}}{{DH}}\) (3).
Theo giả thiết \(\dfrac{{HD}}{{AH}} = \dfrac{1}{2}\) suy ra \(\dfrac{{HD}}{{AH + HD}} = \dfrac{1}{{2 + 1}}\) hay \(\dfrac{{HD}}{{AD}} = \dfrac{1}{3}\), suy ra \(AD = 3HD\).
Thay vào (3) ta được: \(\tan B.\tan C = \dfrac{{3HD}}{{DH}} = 3\).
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
-
A.
$BC = 10$
-
B.
$BC = 11$
-
C.
$BC = 9$
-
D.
$BC = 12$
Đáp án : A
+) Kẻ đường cao $AH$
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp và định lý Py-ta-go để tính cạnh.
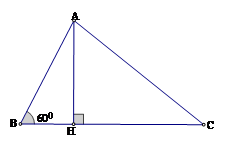
Kẻ đường cao \(AH\).
Xét tam giác vuông \(ABH\), ta có: \(BH = AB.\cos B = AB.\cos {60^0} = 16.\dfrac{1}{2} = 8\)\(AH = AB.\sin B = AB.\sin {60^0} = 16.\dfrac{{\sqrt 3 }}{2} = 8\sqrt 3 \).
Áp dụng định lý Pythago vào tam giác vuông \(AHC\) ta có:
\(H{C^2} = A{C^2} - A{H^2} = {14^2} - {\left( {8\sqrt 3 } \right)^2} = 196 - 192 = 4\). Suy ra \(HC = 2\). Vậy \(BC = CH + HB = 2 + 8 = 10\).
Một máy bay đang bay ở độ cao $10km$ so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là ${15^0}$ thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? ( làm tròn kết quả đến hai chữ số phần thập phân)
-
A.
$37,32\,km$
-
B.
$373,2\,km$
-
C.
$38,32\,km$
-
D.
$37,52\,km$
Đáp án : A
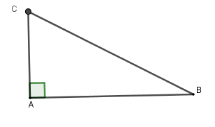
Từ giả thiết suy ra $AC = 10\,\,km;\,\,\widehat B = 15^\circ $.
Xét tam giác $\Delta ABC$ vuông tại $A$ có $AB = AC.\cot B = 10.\cot 15^\circ \approx 37,32\,km$
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai ?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Đáp án : D
Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.
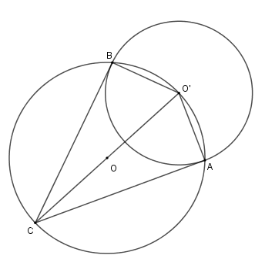
Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$.
Do đó $AB,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau)
Nên A, B, C đúng.
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
-
A.
\(A{B^2}\)
-
B.
\(B{C^2}\)
-
C.
\(A{C^2}\)
-
D.
\(A{M^2}\)
Đáp án : A
Sử dụng hệ quả về góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
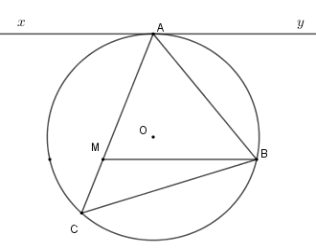
Ta có \(\widehat {yAB} = \widehat {ACB}\) (hệ quả) mà \(\widehat {yAB} = \widehat {ABM}\) (so le trong) nên \(\widehat {ACB} = \widehat {ABM} \Rightarrow \Delta AMB\backsim\Delta ABC\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow AM.AC = A{B^2}\) .
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Đáp án : D
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
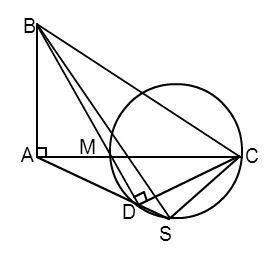
+) Ta có: \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn đường kính $MC$ \( \Rightarrow \widehat {MDC} = {90^0}\) (tính chất góc nội tiếp).
Xét tứ giác $ABCD$ ta có:
Góc $BAC$ và góc $BDC$ cùng nhìn đoạn $BC$ dưới góc \({90^0}.\)
\( \Rightarrow \) $ABCD$ là tứ giác nội tiếp (dhnb) \( \Rightarrow \) phương án A đúng.
+) Xét tứ giác $ABCD$ nội tiếp ta có\(\widehat {ABD} = \widehat {ACD}\) (cùng nhìn đoạn $AD$ )\( \Rightarrow \) phương án B đúng.
+) Xét đường tròn đường kính $MC$ ta có $4$ điểm $M,C,D,S$ cùng thuộc đường tròn.
\( \Rightarrow \) Tứ giác $MCSD$ là tứ giác nội tiếp.
\( \Rightarrow \widehat {ADM} = \widehat {SCM}\) (góc ngoài tại $1$ đỉnh bằng góc trong tại đỉnh đối diện). $\left( 1 \right)$
Vì tứ giác $ABCD$ nội tiếp (cmt) \( \Rightarrow \widehat {ACB} = \widehat {ADB}\) (cùng nhìn đoạn$AB$ ) $\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ \( \Rightarrow \widehat {BCA} = \widehat {ACS}\;\;\;\left( { = \widehat {ADB}} \right).\)
Hay $CA$ là phân giác của \(\widehat {SCB} \Rightarrow \) phương án C đúng.
+) Giả sử tứ giác $ABCS$ là tứ giác nội tiếp \( \Rightarrow \widehat {ASB} = \widehat {BCA}\) (hai góc cùng nhìn đoạn $AB$ ).
Mà \(\widehat {ACB} = \widehat {BDA};\;\;\;\widehat {BAD} \ne \widehat {BSA}\) (xét trong đường tròn đường kính $CM$ )
\( \Rightarrow \widehat {ASB} \ne \widehat {BCA} \Rightarrow \) tứ giác $ABCS$ không là tứ giác nội tiếp \( \Rightarrow \)phương án D sai.
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA, MB\) với \(\left( O \right)\) tại \(A\) và \(B.\) Qua \(A\) vẽ đường thẳng song song với \(MB\) cắt đường tròn tại \(C.\)

Nối \(C\) với \(M\) cắt đường tròn \(\left( O \right)\) tại \(D.\) Nối \(A\) với \(D\) cắt \(MB\) tại \(E.\) Chọn câu đúng
-
A.
\(ME = 2EB\)
-
B.
\(2ME = EB\)
-
C.
\(ME = EB.\)
-
D.
\(3ME = 2EB\)
Đáp án : C
Sử dụng tính chất góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn 1 cung.
Sử dụng tính chất tam giác đồng dạng.
Xét \(\Delta ABE\) và \(\Delta BDE\) có:
+ \(\widehat E\) chung.
+ \(\widehat {BAE} = \widehat {DBE}\) (góc nội tiếp và góc giữa tia tiếp tuyến và dây cung cùng chắn cung $BD$ )
Do đó ta có \(\Delta ABE \backsim \Delta BDE\,\left( {g.g} \right)\).
\( \Rightarrow \dfrac{{AE}}{{BE}} = \dfrac{{BE}}{{DE}} \Rightarrow E{B^2} = AE.DE\,\,\left( 1 \right).\)
Ta có: \(MB//AC \Rightarrow \widehat {EMD} = \widehat {DCA}\) (hai góc so le trong)
Mà \(\widehat {DCA} = \widehat {MAD}\) (góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn cung \(AD\))
Do đó \(\widehat {EMD} = \widehat {MAD}\).
Xét \(\Delta MEA\) và \(\Delta DEM\) có:
\(\widehat E\) chung.
\(\widehat {EMD} = \widehat {MAD}\) (cmt)
Suy ra \(\Delta MEA \backsim \Delta DEM\,.\)
Do đó
\(\dfrac{{ME}}{{DE}} = \dfrac{{EA}}{{EM}} \Rightarrow M{E^2} = DE.EA\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(2\) ta nhận được \(E{B^2} = E{M^2} \Rightarrow EB = EM.\)
Cho \(A\) là điểm cố định trên đường tròn \(\left( {O;R} \right).\) Gọi \(AB\) và \(AC\) là hai dây cung thay đổi trên đường tròn \(\left( O \right)\) thỏa mãn \(\sqrt {AB.AC} = R\sqrt 3 .\) Khi đó vị trí của \(B,\,C\) trên \(\left( O \right)\) để diện tích \(\Delta ABC\) lớn nhất là:
-
A.
\(\Delta ABC\) cân
-
B.
\(\Delta ABC\) đều.
-
C.
\(\Delta ABC\) vuông cân
-
D.
\(\Delta ABC\) vuông
Đáp án : B
Kẻ \(AH \bot BC,\,OI \bot BC\), đường kính $AD.$
Sử dụng tính chất góc nội tiếp chắn nửa đường tròn để chứng minh \(\widehat {ABD} = {90^0} \Rightarrow \Delta ABD \backsim \Delta AHC\).
Tính độ dài \(AH\) từ tính chất hai tam giác đồng dạng, từ đó suy ra điều kiện để diện tích tam giác \(ABC\) lớn nhất.
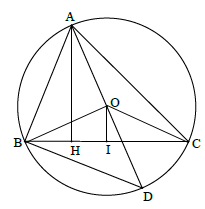
Kẻ \(AH \bot BC,\,OI \bot BC\), đường kính $AD.$
Ta chứng minh được \(\Delta AHC \backsim \Delta ABD\,\left( {g - g} \right).\)
Do đó \(\dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{AD}} \Rightarrow AH.AD = AB.AC \)\(\Rightarrow AB.AC = 2R.AH\,\,\left( 1 \right).\)
Theo giả thiết \(\sqrt {AB.AC} = R\sqrt 3 ,\) nên \(AB.AC = 3{R^2}\,\,\left( 2 \right).\)
Thay \(\left( 2 \right)\) và \(\left( 1 \right)\) ta có \(AH = \dfrac{{3R}}{2}.\)
Lại có \(OI + OA \ge AI \ge AH\) nên \(OI \ge AH - OA = \dfrac{{3R}}{2} - R = \dfrac{R}{2}.\)
Do \(AH = \dfrac{{3R}}{2}\) là giá trị không đổi nên \({S_{ABC}}\) lớn nhất khi \(BC\) lớn nhất \( \Leftrightarrow OI\) nhỏ nhất
\( \Leftrightarrow OI = \dfrac{R}{2} \Leftrightarrow BC \bot OA \Rightarrow \Delta ABC\) cân tại \(A\).
Mà \(OI = \dfrac{R}{2} \Rightarrow \sin \widehat {OBI} \)\(= \dfrac{{OI}}{{OB}} = \dfrac{1}{2}\)\( \Rightarrow \widehat {OBI} = \widehat {OCI} = {30^0} \)\(\Rightarrow \widehat {BOC} \)\(= {120^0}\)$ \Rightarrow \widehat {BAC} = {60^0}$
Vậy \(\Delta ABC\) đều.
Cho đường thẳng $d:y = x + 2;d':y = - 2x + 5$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $B$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành. Khi đó diện tích tam giác $AMB$ là:
-
A.
$\dfrac{{27}}{6}$ ( đvdt)
-
B.
$27$( đvdt)
-
C.
$\dfrac{{27}}{2}$ (đvdt)
-
D.
$\dfrac{{27}}{4}$(đvdt)
Đáp án : D
- Xác định giao điểm 2 đường thẳng đã cho
- Dựng đường cao của tam giác được tạo thành
- Tính độ dài các đoạn thẳng
- Tính diện tích tam giác.
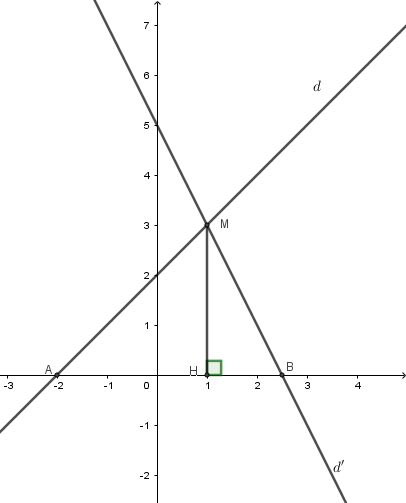
Xét phương trình hoành độ giao điểm của ${d_1};{d_2}$
$x + 2 = - 2x + 5 \Leftrightarrow x = 1 \Rightarrow y = 3 \Rightarrow {d_1} \cap {d_2}$ tại $ M(1;3)$
Gọi $H$ là chân đường vuông góc kẻ từ $M$ tới $Ox$. Suy ra $MH = 3$
$d \cap Ox$ tại $ A( - 2;0) \Rightarrow OA = 2$
$d' \cap Ox$ tại $ B\left( {\dfrac{5}{2};0} \right) \Rightarrow OB = \dfrac{5}{2}$
$\Rightarrow AB = OA+OB=2 + \dfrac{5}{2} = \dfrac{9}{2}$
${S_{MAB}} = \dfrac{1}{2}AB.MH = \dfrac{1}{2}.\dfrac{9}{2}.3 = \dfrac{{27}}{4}\,(dvdt)$
Với \(x;\,\,y;\,\,z\) là các số thực thỏa mãn \(x + y + z + xy + yz + zx = 6\). Tìm giá trị nhỏ nhất của biểu thức:
\(P = \sqrt {4 + {x^4}} + \sqrt {4 + {y^4}} + \sqrt {4 + {z^4}} \).
-
A.
\({{\rm P}_{\min }} = \sqrt 5 \)
-
B.
\({{\rm P}_{\min }} = 3\sqrt 5 \)
-
C.
\({{\rm P}_{\min }} = 5\sqrt 3 \)
-
D.
\({{\rm P}_{\min }} = 3\)
Đáp án : B
Sử dụng bất đẳng thức Bunhiacopxki và mở rộng của bất đẳng thức
+ Bất đẳng thức Bunhiacopxki cho bốn số \(x;\,\,y;\,\,z;\,\,t\): \(\sqrt {\left({{x^2} + {y^2}} \right)\left( {{z^2} + {t^2}} \right)} \ge xz + yt.\)
+ Phát triển tử bất đẳng thức trên để được bất đẳng thức :
$\sqrt {{x^2} + {y^2}} + \sqrt {{z^2} + {t^2}} \ge \sqrt {{{\left( {x + z} \right)}^2} + {{\left( {y + t} \right)}^2}}$ (*)
Từ đó sử dụng để làm bài.
Trước hết ta chứng minh với $x;y;z;t$ bất kì thì
\(\sqrt {{x^2} + {y^2}} + \sqrt {{z^2} + {t^2}} \ge \sqrt {{{\left( {x + z} \right)}^2} + {{\left( {y + t} \right)}^2}} \) (*).
Thật vậy, bất đẳng thức (*) tương đương với
\({x^2} + {y^2} + {z^2} + {t^2} + 2\sqrt {\left( {{x^2} + {y^2}} \right)\left( {{z^2} + {t^2}} \right)} \)\( \ge {x^2} + 2xz + {z^2} + {y^2} + 2yt + {t^2}\)
\( \Leftrightarrow \sqrt {\left( {{x^2} + {y^2}} \right)\left( {{z^2} + {t^2}} \right)} \ge xz + yt\)
Đúng vì theo bất đẳng thức Bunhia cốp xki
\(\sqrt {\left( {{x^2} + {y^2}} \right)\left( {{z^2} + {t^2}} \right)} \ge \sqrt {{{\left( {xz + yt} \right)}^2}} \)\(= \left| {\left( {xz + yt} \right)} \right| \ge \left( {xz + yt} \right)\).
Áp dụng (*) ta có
\(P = \sqrt {4 + {x^4}} + \sqrt {4 + {y^4}} + \sqrt {4 + {z^4}} \)\( \ge \sqrt {{{\left( {2 + 2} \right)}^2} + {{\left( {{x^2} + {y^2}} \right)}^2}} + \sqrt {4 + {z^4}} \)\( \ge \sqrt {{{\left( {2 + 2 + 2} \right)}^2} + {{\left( {{x^2} + {y^2} + {z^2}} \right)}^2}} \)
\( = \sqrt {36 + {{\left( {{x^2} + {y^2} + {z^2}} \right)}^2}} \).
Ta có \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} + {\left( {x - y} \right)^2} + {\left( {y - z} \right)^2} + {\left( {z - x} \right)^2} \ge 0\)
\( \Rightarrow 3{x^2} + 3{y^2} + 3{z^2} + 3 \ge 2x + 2y + 2z + 2xy + 2yz + 2zx\)
\( \Rightarrow 3{x^2} + 3{y^2} + 3{z^2} + 3 \ge 2.6 = 12 \)\(\Rightarrow {x^2} + {y^2} + {z^2} \ge 3.\)
Từ đó \(P \ge \sqrt {36 + 9} = 3\sqrt 5 \).
Dấu “=” xảy ra \(x = y = z = 1\).
Vậy \({{\rm P}_{\min }} = 3\sqrt 5 .\)
Cho phương trình: \({x^2} - 2mx + 2m - 1 = 0\) .
Tìm $m$ để phương trình có $2$ nghiệm phân biệt thỏa mãn: \(2\left( {x_1^2 + x_2^2} \right) - 5{x_1}{x_2} = - 1\).
-
A.
\(m = 1\)
-
B.
\(m = \dfrac{5}{4}\)
-
C.
\(m = - 4\)
-
D.
\(m = \dfrac{{ - 7}}{4}\)
Đáp án : B
- Trước tiên ta tìm điều kiện của \(m\) để phương trình đã cho có hai nghiệm phân biệt: \({x_1},{x_2}\,(\Delta ' > 0)\).
- Ta biến đổi biểu thức \(2({x_1}^2 + {x_2}^2) - 5{x_1}{x_2}\) về biểu thức có chứa ${x_1} + {x_2}$ và ${x_1}{x_2}$ rồi từ đó ta tìm được giá trị của \(m\).
- Đối chiếu với điều kiện xác định của \(m\) để tìm được giá trị thỏa mãn yêu cầu của bài toán.
Xét phương trình: \({x^2} - 2mx + 2m - 1 = 0\) ta có:
$\Delta ' = {m^2} - 1.\left( {2m - 1} \right) = {m^2} - 2m + 1 = {(m - 1)^2}$
Để phương trình có hai nhiệm phân biệt thì $\Delta ' > 0 \Leftrightarrow {(m - 1)^2} > 0 \Leftrightarrow m \ne 1$ .
Ta có:
\(\begin{array}{l}2({x_1}^2 + {x_2}^2) - 5{x_1}{x_2} = - 1\\ \Leftrightarrow 2{\rm{[}}{\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}{\rm{]}} - 5{x_1}{x_2} = - 1\\ \Leftrightarrow 2{\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} - 5{x_1}{x_2} = - 1\\ \Leftrightarrow 2{\left( {{x_1} + {x_2}} \right)^2} - 9{x_1}{x_2} = - 1\,\,\,(*)\end{array}\)
Áp dụng hệ thức Vi-et ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = 2m - 1\end{array} \right.$ thay vào (*) ta được:
$\begin{array}{l}2{(2m)^2} - 9\left( {2m - 1} \right) = - 1\\ \Leftrightarrow 2.4{m^2} - 18m + 9 + 1 = 0\\ \Leftrightarrow 8{m^2} - 18m + 10 = 0\\ \Leftrightarrow 4{m^2} - 9m + 5 = 0\\ \Leftrightarrow (m - 1)(4m - 5) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\,(ktm)\\m = \dfrac{5}{4}\,(tm)\end{array} \right.\end{array}$
Vậy với $m = \dfrac{5}{4}$ thì yêu cầu của bài toán được thỏa mãn.