Đề kiểm tra học kì 2 Toán 9 - Đề số 4
Đề bài
So sánh hai số $5\sqrt 3 $ và $4\sqrt 5 $
-
A.
$5\sqrt 3 > 4\sqrt 5 $
-
B.
$5\sqrt 3 = 4\sqrt 5 $
-
C.
$5\sqrt 3 \ge 4\sqrt 5 $
-
D.
$5\sqrt 3 < 4\sqrt 5 $
Chọn khẳng định đúng. Nếu phương trình $a{x^2} = mx + n$ vô nghiệm thì đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$
-
A.
Cắt nhau tại hai điểm
-
B.
Tiếp xúc với nhau
-
C.
Không cắt nhau
-
D.
Cắt nhau tại gốc tọa độ
Biêt chu vi đường tròn là \(C = 36\pi (cm)\). Tính đường kính của đường tròn.
-
A.
$18(cm)$
-
B.
$14(cm)$
-
C.
$36(cm)$
-
D.
$20 (cm)$
Cho các biểu thức với $A < 0$ và $B \ge 0$ , khẳng định nào sau đây là đúng?
-
A.
$\sqrt {{A^2}B} = A\sqrt B $
-
B.
$\sqrt {{A^2}B} = - A\sqrt B $
-
C.
$\sqrt {{A^2}B} = -B\sqrt A $
-
D.
$\sqrt {{A^2}B} = B\sqrt A $
Chọn khẳng định đúng về đồ thị hàm số \(y = ax + b(a \ne 0).\)
-
A.
Là đường thẳng đi qua gốc tọa độ
-
B.
Là đường thẳng song song với trục hoành
-
C.
Là đường thẳng đi qua hai điểm \(A(0;b),B\left( { - \dfrac{b}{a};0} \right)\) với \(b \ne 0\)
-
D.
Là đường cong đi qua gốc tọa độ
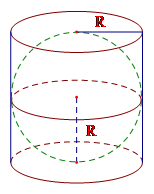
Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu). Tính tỉ số giữa diện tích mặt cầu và diện tích xung quanh của hình trụ.
-
A.
\(3\)
-
B.
\(1\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(2\)
Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(BC.\) Lấy điểm \(A\) trên tia đối của tia \(CB.\) Kẻ tiếp tuyến $AF,Bx$ của nửa đường tròn \(\left( O \right)\) (với \(F\) là tiếp điểm). Tia \(AF\) cắt tia \(Bx\) của nửa đường tròn tại \(D.\) Khi đó tứ giác \(OBDF\) là:
-
A.
Hình thang
-
B.
Tứ giác nội tiếp
-
C.
Hình thang cân
-
D.
Hình bình hành
Cho mặt cầu có thể tích \(V = 288\pi \,\left( {c{m^3}} \right)\) . Tính đường kính mặt cầu.
-
A.
\(6\,cm\)
-
B.
\(12\,cm\)
-
C.
\(8\,cm\)
-
D.
\(16\,cm\)
Cho $\left( {O;R} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm $A$ khi
-
A.
$d \bot OA$ tại $A$ và $A \in \left( O \right)$
-
B.
$d \bot OA$
-
C.
$A \in \left( O \right)$
-
D.
$d{\rm{//}}OA$
Phương trình \(\sqrt {x - 5} = \sqrt {3 - x} {\rm{ }}\) có bao nhiêu nghiệm?
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(2\)
-
D.
\(3\)
Gọi ${x_1};{x_2}$ là nghiệm của phương trình ${x^2} - 5x + 2 = 0$. Không giải phương trình, tính giá trị của biểu thức $A = x_1^2 + x_2^2$
-
A.
$20$
-
B.
$21$
-
C.
$22$
-
D.
$23$
Cho một số có hai chữ số . Chữ số hàng chục lớn hơn chữ số hàng đơn vị là $5$. Nếu đổi chỗ hai chữ số cho nhau ta được một số bằng $\dfrac{3}{8}$ số ban đầu. Tìm tích các chữ số của số ban đầu.
-
A.
$12$
-
B.
$16$
-
C.
$14$
-
D.
$6$
Hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$ cắt nhau khi
-
A.
$a \ne a'$
-
B.
$\left\{ \begin{array}{l}a \ne a'\\b \ne b'\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$
-
D.
$\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$
Tìm điều kiện của $x$ để căn thức \(\sqrt {\dfrac{1}{{x - 1}}} \) có nghĩa.
-
A.
$x \ge 1$
-
B.
\(x < 1\)
-
C.
\(x > 1\)
-
D.
\(x = 1\)
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
-
A.
Đường thẳng $BC$ cắt đường tròn $\left( {C;CA} \right)$ tại một điểm
-
B.
$AB$ là cát tuyến của đường tròn $\left( {C;CA} \right)$
-
C.
$AB$ là tiếp tuyến của $\left( {C;CA} \right)$
-
D.
$BC$ là tiếp tuyến của $\left( {C;CA} \right)$
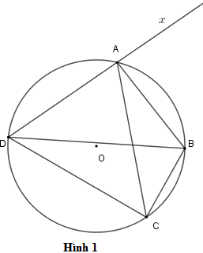
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) (hình \(1\) ). Chọn khẳng định sai?
-
A.
\(\widehat {BDC} = \widehat {BAC}\)
-
B.
\(\widehat {ABC} + \widehat {ADC} = 180^\circ \)
-
C.
\(\widehat {DAB} = \widehat {BAx}\)
-
D.
\(\widehat {BCA} = \widehat {BDA}\)
Cho tam giác $ABC$ nhọn nội tiếp đường tròn $\left( O \right)$ . $M$ là điểm thuộc cung nhỏ $AC$ (cung \(CM < \) cung \(AM\)). Vẽ $MH$ vuông góc với $BC$ tại $H$ , vẽ $MI$ vuông góc với $AC$ tại $I$ . Chọn câu đúng :
-
A.
$MIHC$ là hình chữ nhật.
-
B.
$MIHC$ là hình vuông.
-
C.
$MIHC$ không là tứ giác nội tiếp.
-
D.
$MIHC$ là tứ giác nội tiếp.
Một ô tô đi quãng đường $AB$ với vận tốc $50\,\,km/h$ , rồi đi tiếp quãng đường $BC$ với vận tốc $45km/h.$ Biết quãng đường tổng cộng dài $165\,\,km$ và thời gian ô tô đi trên quãng đường $AB$ ít hơn thời gian đi trên quãng đường $BC$ là $30$ phút. Tính thời gian ô tô đi trên đoạn đường $AB$.
-
A.
$2$ giờ
-
B.
$1,5$ giờ
-
C.
$1$ giờ
-
D.
$3$ giờ
Tâm đường tròn nội tiếp của tam giác là
-
A.
giao của ba đường phân giác góc trong tam giác
-
B.
giao ba đường trung trực của tam giác
-
C.
trọng tâm tam giác
-
D.
trực tâm tam giác
Cho tam giác \(ABC\) có \(BC\) cố định và góc \(A\) bằng \(50^\circ \). Gọi \(D\) là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm \(D\).
-
A.
Một cung chứa góc \(115^\circ \) dựng trên đoạn \(BC\).
-
B.
Một cung chứa góc \(115^\circ \) dựng trên đoạn \(AC\).
-
C.
Hai cung chứa góc \(115^\circ \) dựng trên đoạn \(AB\).
-
D.
Hai cung chứa góc \(115^\circ \) dựng trên đoạn \(BC\).
Giá trị của biểu thức \(2\sqrt {\dfrac{{16a}}{3}} - 3\sqrt {\dfrac{a}{{27}}} - 6\sqrt {\dfrac{{4a}}{{75}}} \) là
-
A.
$\dfrac{{23\sqrt {3a} }}{{15}}$
-
B.
$\dfrac{{\sqrt {3a} }}{{15}}$
-
C.
$\dfrac{{23\sqrt a }}{{15}}$
-
D.
$\dfrac{{3\sqrt {3a} }}{{15}}$
Rút gọn biểu thức: $A = \left( {\dfrac{{\sqrt x }}{2} - \dfrac{1}{{2\sqrt x }}} \right)\left( {\dfrac{{x - \sqrt x }}{{\sqrt x + 1}} - \dfrac{{x + \sqrt x }}{{\sqrt x - 1}}} \right)$ v ới \(x > 0;\,\,x \ne 1.\)
-
A.
\(A = - 2\sqrt x \)
-
B.
\(A = 2\sqrt x \)
-
C.
\(A = - \sqrt x \)
-
D.
\(A = 4\sqrt x \)
Giải phương trình \(\sqrt {2{x^2} - 4x + 5} = x - 2\) ta được nghiệm là
-
A.
\(x = 1\)
-
B.
\(x = 3\)
-
C.
\(x = 2\)
-
D.
Phương trình vô nghiệm
Với giá trị nào của m thì đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung?
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = - 1$
-
D.
$m = 2$
Cho đường thẳng $d:y = 3x - \dfrac{1}{2}$. Giao điểm của $d$ với trục tung là
-
A.
$A\left( {\dfrac{1}{6};0} \right)$
-
B.
$B\left( {0;\dfrac{1}{2}} \right)$
-
C.
$C\left( {0;\dfrac{{ - 1}}{6}} \right)$
-
D.
$D\left( {0; - \dfrac{1}{2}} \right)$
Cho hai đường thẳng $d:y = \left( {m + 2} \right)x - m$ và $d':y = - 2x - 2m + 1$ .Với giá trị nào của $m$ thì $d \equiv d'$?
-
A.
$m = - 2$
-
B.
$m = - 4$
-
C.
$m = 2$
-
D.
Không có $m$ thỏa mãn
Cho hệ phương trình: $\left\{ \begin{array}{l}\left( {a + 1} \right)x - y = a + 1\begin{array}{*{20}{c}}{}&{\left( 1 \right)}\end{array}\\x + \left( {a - 1} \right)y = 2\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{}&{\left( 2 \right)}\end{array}}&{}\end{array}\end{array} \right.$
( $a$ là tham số)
Với $a \ne 0$ hệ có nghiệm duy nhất $\left( {x;y} \right)$. Tìm các số nguyên $a$ để hệ phương trình có nghiệm nguyên
-
A.
$a = 1$
-
B.
$a = - 1$
-
C.
$a \ne \left\{ { \pm 1} \right\}$
-
D.
$a = \pm 1$
Hai xí nghiệp theo kế hoạch phải làm tổng cộng $360$ dụng cụ. Trên thực tế, xí nghiệp $1$ vượt mức $12\% $ , xí nghiệp $2$ vượt mức $10\% $ , do đó cả hai xí nghiệp làm tổng cộng $400$ dụng cụ. Tính số dụng cụ xí nghiệp $2$ phải làm theo kế hoạch
-
A.
\(160\) dụng cụ
-
B.
\(200\) dụng cụ.
-
C.
\(120\) dụng cụ.
-
D.
\(240\) dụng cụ.
Hai giá sách có $450$ cuốn. Nếu chuyển $50$ cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên giá thứ hai bằng $\dfrac{4}{5}$ số sách ở giá thứ nhất. Tính số sách trên giá thứ hai.
-
A.
$150$ cuốn
-
B.
$300$ cuốn
-
C.
$200$ cuốn
-
D.
$250$ cuốn
Lập phương trình nhận hai số $3 - \sqrt 5 $ và $3 + \sqrt 5 $ làm nghiệm.
-
A.
${x^2} - 6x - 4 = 0$
-
B.
${x^2} - 6x + 4 = 0$
-
C.
${x^2} + 6x + 4 = 0$
-
D.
$ - {x^2} - 6x + 4 = 0$
Tìm giá trị của \(m\) để phương trình \({x^2} + (4m + 1)x + 2(m - 4) = 0\) c ó hai nghiệm \({x_1},{x_2}\) và biểu thức \(A = {\left( {{x_1} - {x_2}} \right)^2}\) đạt giá trị nhỏ nhất.
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = 2$
-
D.
$m = 3$
Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt
-
A.
$m = 2$
-
B.
$m = - 2$
-
C.
$m = 4$
-
D.
$m \in \mathbb{R}$
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai ?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Cho hình vuông \(ABCD\). Trên cạnh \(BC\) lấy điểm \(E\) , trên tia đối của tia \(CD\) lấy điểm \(F\) sao cho \(CE = CF\). Gọi \(M\) là giao điểm của hai đường thẳng \(DE\) và \(BF\). Tìm quỹ tích của điểm \(M\) khi \(E\) di động trên cạnh \(BC\).
-
A.
Nửa đường tròn đường kính $BD$ .
-
B.
Cung \(BC\) của đường tròn đường kính $BD$.
-
C.
Cung \(BC\) của đường tròn đường kính $BD$ trừ điểm \(B,C\) .
-
D.
Đường tròn đường kính $BD$ .
Cho tam giác $ABC$ vuông tại $A$ và điểm $D$ nằm giữa $A$ và $B$ . Đường tròn đường kính $BD$ cắt $BC$ tại $E$. Các đường thẳng $CD$ , $AE$ lần lượt cắt đường tròn tại các điểm thứ hai là $F$ và $G$. Khi đó, kết luận không đúng là:
-
A.
$\Delta ABC\backsim\Delta EBD$.
-
B.
Tứ giác $ADEC$ là tứ giác nội tiếp.
-
C.
Tứ giác $AFBC$ không là tứ giác nội tiếp.
-
D.
Các đường thẳng $AC,DE$ và $BF$ đồng quy.
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Cho tam giác $ABC$ vuông tại $A$ , cạnh $AB = 5\,\,cm$ , \(\widehat B = {60^ \circ }\). Đường tròn tâm $I$ , đường kính $AB$ cắt $BC$ ở $D$ . Chọn khẳng định sai?
-
A.
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là $\dfrac{\pi }{6}\,\,\left( {cm} \right)$
-
B.
$AD \bot BC$
-
C.
$D$ thuộc đường tròn đường kính \(AC\)
-
D.
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là \(\dfrac{{5\pi }}{6}\,\,\left( {cm} \right)\)
Cho hình chữ nhật \(ABCD\) có \(AB = 4\,cm;AD = 3\,cm\) . Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) .
-
A.
\(25\pi \)
-
B.
\(\dfrac{{25\pi }}{8}\)
-
C.
\(25\)
-
D.
\(\dfrac{{25\pi }}{4}\)
Cho tam giác $ABC$ vuông tại $A$. Tính \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
-
A.
\(0\)
-
B.
\(1\)
-
C.
\( - 1\)
-
D.
\(2\)
Cho đoạn thẳng $AB = 2a$ và trung điểm $O$ của nó. Trên nửa mặt phẳng bờ $AB$ vẽ các tia $Ax,By\;$ vuông góc với $AB.$ Qua \(O\) vẽ một tia cắt tia \(Ax\) tại $M$ sao cho $\widehat {AOM} = \alpha < {90^0}$ . Qua $O$ vẽ tia thứ hai cắt tia $By$ tại $N$ sao cho \(\widehat {MON} = 90^\circ \) . Khi đó, diện tích tam giác \(MON\) là
-
A.
\(\dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
-
B.
\(\dfrac{{{a^2}}}{{\sin \alpha .\cos \alpha }}\)
-
C.
\(\dfrac{a}{{2\sin \alpha .\cos \alpha }}\)
-
D.
\(\dfrac{{2{a^2}}}{{\sin \alpha .\cos \alpha }}\)
Lời giải và đáp án
So sánh hai số $5\sqrt 3 $ và $4\sqrt 5 $
-
A.
$5\sqrt 3 > 4\sqrt 5 $
-
B.
$5\sqrt 3 = 4\sqrt 5 $
-
C.
$5\sqrt 3 \ge 4\sqrt 5 $
-
D.
$5\sqrt 3 < 4\sqrt 5 $
Đáp án : D
Đưa thừa số vào trong dấu căn để so sánh hai số $\sqrt A < \sqrt B \Leftrightarrow 0 \le A < B$.
Đưa thừa số vào trong dấu căn
+) $A\sqrt B = \sqrt {{A^2}B} $ với $A \ge 0$ và $B \ge 0$
+) $A\sqrt B = - \sqrt {{A^2}B} $ với $A < 0$ và $B \ge 0$
Ta có $5\sqrt 3 = \sqrt {{5^2}.3} = \sqrt {25.3} = \sqrt {75} $; $4\sqrt 5 = \sqrt {{4^2}.5} = \sqrt {16.5} = \sqrt {80} $
Vì $75 < 80 $ nên $\sqrt {75} < \sqrt {80} $ hay $ 5\sqrt 3 < 4\sqrt 5 $
Chọn khẳng định đúng. Nếu phương trình $a{x^2} = mx + n$ vô nghiệm thì đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$
-
A.
Cắt nhau tại hai điểm
-
B.
Tiếp xúc với nhau
-
C.
Không cắt nhau
-
D.
Cắt nhau tại gốc tọa độ
Đáp án : C
Đường thẳng $d:y = mx + n$ và parabol $\left( P \right):y = a{x^2}$ không cắt nhau khi phương trình $a{x^2} = mx + n$ vô nghiệm.
Biêt chu vi đường tròn là \(C = 36\pi (cm)\). Tính đường kính của đường tròn.
-
A.
$18(cm)$
-
B.
$14(cm)$
-
C.
$36(cm)$
-
D.
$20 (cm)$
Đáp án : C
Sử dụng công thức chu vi đường tròn đường kính \(d = 2R\) là \(C = \pi d\,\)
Chu vi \(C = \pi d = 36\pi \Rightarrow d = 36\). Vậy đường kính cần tìm là \(36(cm)\) .
Cho các biểu thức với $A < 0$ và $B \ge 0$ , khẳng định nào sau đây là đúng?
-
A.
$\sqrt {{A^2}B} = A\sqrt B $
-
B.
$\sqrt {{A^2}B} = - A\sqrt B $
-
C.
$\sqrt {{A^2}B} = -B\sqrt A $
-
D.
$\sqrt {{A^2}B} = B\sqrt A $
Đáp án : B
Với hai biểu thức $A,B$ mà $B \ge 0$, ta có $\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,{\rm{khi}}\,\,A \ge 0\\ - A\sqrt B \,{\rm{khi}}\,A < 0\end{array} \right.$
Chọn khẳng định đúng về đồ thị hàm số \(y = ax + b(a \ne 0).\)
-
A.
Là đường thẳng đi qua gốc tọa độ
-
B.
Là đường thẳng song song với trục hoành
-
C.
Là đường thẳng đi qua hai điểm \(A(0;b),B\left( { - \dfrac{b}{a};0} \right)\) với \(b \ne 0\)
-
D.
Là đường cong đi qua gốc tọa độ
Đáp án : C
Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng
Trường hợp 1: Nếu \(b = 0\) ta có hàm số \(y = ax\). Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a).\)
Trường hợp 2: Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
Cho một hình cầu và hình trụ ngoại tiếp nó (đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu). Tính tỉ số giữa diện tích mặt cầu và diện tích xung quanh của hình trụ.

-
A.
\(3\)
-
B.
\(1\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(2\)
Đáp án : B
Sử dụng công thức diện tích mặt cầu $S = 4\pi {R^2}$ và diện tích xung quanh của hình trụ \({S_{xq}} = 2\pi Rh\)
Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên \(h = 2R\) với \(R\) là bán kính hình cầu và cũng là bán kính đáy của hình trụ.
Diện tích mặt cầu \(S = 4\pi {R^2}\) , diện tích xung quanh của hình trụ \({S_{xq}} = 2\pi Rh = 2\pi R.2R = 4\pi {R^2}\)
Tỉ số giữa d iện tích mặt cầu và diện tích xung quanh của hình trụ là \(\dfrac{S}{{{S_{xq}}}} = \dfrac{{4\pi {R^2}}}{{4\pi {R^2}}} = 1\) .
Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(BC.\) Lấy điểm \(A\) trên tia đối của tia \(CB.\) Kẻ tiếp tuyến $AF,Bx$ của nửa đường tròn \(\left( O \right)\) (với \(F\) là tiếp điểm). Tia \(AF\) cắt tia \(Bx\) của nửa đường tròn tại \(D.\) Khi đó tứ giác \(OBDF\) là:
-
A.
Hình thang
-
B.
Tứ giác nội tiếp
-
C.
Hình thang cân
-
D.
Hình bình hành
Đáp án : B
Tứ giác có tổng một cặp góc đối bằng \({180^0}\) là tứ giác nội tiếp.
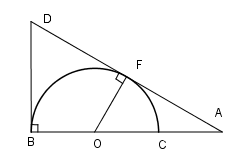
Ta có \(\widehat {DBO} = {90^0}\) và \(\widehat {DFO} = {90^0}\) ( tính chất tiếp tuyến).
Tứ giác \(OBDF\) có \(\widehat {DBO} + \widehat {DFO} = {90^0} + {90^0} = {180^0}\) nên nội tiếp được trong một đường tròn.
Cho mặt cầu có thể tích \(V = 288\pi \,\left( {c{m^3}} \right)\) . Tính đường kính mặt cầu.
-
A.
\(6\,cm\)
-
B.
\(12\,cm\)
-
C.
\(8\,cm\)
-
D.
\(16\,cm\)
Đáp án : B
Sử dụng công thức thể tích khối cầu $V = \dfrac{4}{3}\pi {R^3}$ để tính bán kính, từ đó suy ra đường kính của mặt cầu.
Ta có:
\(V = \dfrac{4}{3}\pi {R^3} = 288\pi \)
\({R^3} = 216\)
\(R = 6\,cm\)
Từ đó đường kính mặt cầu là \(d = 2R = 2.6 = 12\,cm\).
Cho $\left( {O;R} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm $A$ khi
-
A.
$d \bot OA$ tại $A$ và $A \in \left( O \right)$
-
B.
$d \bot OA$
-
C.
$A \in \left( O \right)$
-
D.
$d{\rm{//}}OA$
Đáp án : A
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Phương trình \(\sqrt {x - 5} = \sqrt {3 - x} {\rm{ }}\) có bao nhiêu nghiệm?
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(2\)
-
D.
\(3\)
Đáp án : B
Giải phương trình dạng \(\sqrt A = \sqrt B \)
ĐK: \(A \ge 0\) (hoặc \(B \ge 0\) )
Khi đó \(\sqrt A = \sqrt B \Leftrightarrow A = B\)
So sánh với điều kiện rồi kết luận.
Điều kiện: \(x \ge 5\)
Ta có \(\sqrt {x - 5} = \sqrt {3 - x} {\rm{ }}\)\( \Leftrightarrow x - 5 = 3 - x \Leftrightarrow x + x = 3 + 5 \Leftrightarrow 2x = 8 \Leftrightarrow x = 4\,\,\left( {KTM} \right)\)
Vậy phương trình đã cho vô nghiệm.
Gọi ${x_1};{x_2}$ là nghiệm của phương trình ${x^2} - 5x + 2 = 0$. Không giải phương trình, tính giá trị của biểu thức $A = x_1^2 + x_2^2$
-
A.
$20$
-
B.
$21$
-
C.
$22$
-
D.
$23$
Đáp án : B
Bước 1: Sử dụng định lí Viète
Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình $a{x^2} + bx + c = 0\,\,(a \ne 0)$ thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1} \cdot {x_2} = \dfrac{c}{a}\end{array} \right..\)
Bước 2: Sử dụng hằng đẳng thức bình phương của một tổng để biến đổi $A = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}$
Phương trình ${x^2} - 5x + 2 = 0$ có $\Delta = {\left( { - 5} \right)^2} - 4.1.2 = 17 > 0$ nên phương trình có hai nghiệm ${x_1};{x_2}$
Theo định lí Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{-(-5)}{1} = 5\\{x_1}.{x_2} = \frac{2}{1} = 2\end{array} \right.\).
Ta có $A = x_1^2 + x_2^2 = \left(x_1^2 + 2{x_1}{x_2} + x_2^2\right) - 2{x_1}{x_2} = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {5^2} - 2.2 = 21$
Cho một số có hai chữ số . Chữ số hàng chục lớn hơn chữ số hàng đơn vị là $5$. Nếu đổi chỗ hai chữ số cho nhau ta được một số bằng $\dfrac{3}{8}$ số ban đầu. Tìm tích các chữ số của số ban đầu.
-
A.
$12$
-
B.
$16$
-
C.
$14$
-
D.
$6$
Đáp án : C
Gọi số cần tìm là \(\overline {ab} ,\,\,a \in {\mathbb{N}^*},\,\,b \in {\mathbb{N}^*}\), $a,b \le 9$.
Biểu diễn số mới theo ab, từ đó viết các phương trình dựa vào đề bài để lập hệ phương trình.
Sử dụng phương pháp thế để giải hệ phương trình tìm được.
Gọi số cần tìm là \(\overline {ab} ,\,\,a \in {\mathbb{N}^*},\,\,b \in {\mathbb{N}^*}\), $a,b \le 9$.
Đổi chỗ hai chữ số của nó thì được một số mới là \(\overline {ba} \)
Ta có hệ phương trình: $\left\{ \begin{array}{l}a - b = 5\\\overline {ba} = \dfrac{3}{8}\overline {ab} \end{array} \right.$ hay $\left\{ \begin{array}{l}a - b = 5 \;(1)\\b.10 + a = \dfrac{3}{8}\left( {a.10 + b} \right) (2)\end{array}\right.$
Nhân cả hai vế của phương trình (2) với 8, ta được phương trình: \(80b + 8a = 30a + 3b \;(3)\)
Từ phương trình (1) suy ra $a = b + 5$
Thế vào phương trình (3), ta được:
$80b + 8\left( {b + 5} \right) = 30\left( {b + 5} \right) + 3b$
$55b = 110$
$b = 2$ (TM)
Suy ra $a = 2 + 5 = 7$ (TM)
Vậy số cần tìm là $72$ nên tích các chữ số là $2.7 = 14$.
Hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$ cắt nhau khi
-
A.
$a \ne a'$
-
B.
$\left\{ \begin{array}{l}a \ne a'\\b \ne b'\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$
-
D.
$\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$
Đáp án : A
Cho hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$.
\(d\) cắt $d'$\( \Leftrightarrow a \ne a'\).
Tìm điều kiện của $x$ để căn thức \(\sqrt {\dfrac{1}{{x - 1}}} \) có nghĩa.
-
A.
$x \ge 1$
-
B.
\(x < 1\)
-
C.
\(x > 1\)
-
D.
\(x = 1\)
Đáp án : C
\(\sqrt A \) xác định (hay có nghĩa) khi \(A\) lấy giá trị không âm tức là \(A \ge 0.\)
Ngoài ra: \(\dfrac{1}{A} \ge 0 \Leftrightarrow A > 0\)
Ta có \(\sqrt {\dfrac{1}{{x - 1}}} \) có nghĩa \( \Leftrightarrow \dfrac{1}{{x - 1}} \ge 0 \Rightarrow x - 1 > 0\) (vì $1>0$)
\( \Leftrightarrow x > 1\)
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
-
A.
Đường thẳng $BC$ cắt đường tròn $\left( {C;CA} \right)$ tại một điểm
-
B.
$AB$ là cát tuyến của đường tròn $\left( {C;CA} \right)$
-
C.
$AB$ là tiếp tuyến của $\left( {C;CA} \right)$
-
D.
$BC$ là tiếp tuyến của $\left( {C;CA} \right)$
Đáp án : C
Sử dụng cách chứng minh tiếp tuyến
Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $M$ ta chứng minh $OM \bot d$ tại $M$ và $M \in \left( O \right)$.
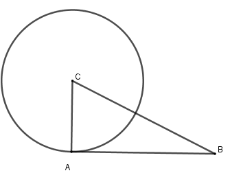
+) Xét tam giác $ABC$ có \(B{C^2} = {5^2} = 25;A{B^2} + A{C^2} = {4^2} + {3^2} = 25; \Rightarrow B{C^2} = A{B^2} + A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại A (định lý Pytago đảo)
\( \Rightarrow AB \bot AC\) mà $A \in \left( {C;CA} \right)$ nên $AB$ là tiếp tuyến của $\left( {C;CA} \right)$
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) (hình \(1\) ). Chọn khẳng định sai?

-
A.
\(\widehat {BDC} = \widehat {BAC}\)
-
B.
\(\widehat {ABC} + \widehat {ADC} = 180^\circ \)
-
C.
\(\widehat {DAB} = \widehat {BAx}\)
-
D.
\(\widehat {BCA} = \widehat {BDA}\)
Đáp án : D
Sử dụng kiến thức hai góc cùng chắn một cung thì bằng nhau.
Sử dụng tính chất tứ giác nội tiếp: Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng \(180^\circ\)
Vì tứ giác \(ABCD\) là tứ giác nội tiếp nên
\(\widehat {BDC} = \widehat {BAC}\) (hai góc nội tiếp cùng chắn cung \(BC\) )
\(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (tổng hai góc đối bằng \(180^\circ \) )
\(\widehat {DAB}\) và \(\widehat {BAx}\) là hai góc kề bù nhưng \(\widehat {DAB} \ne 90^\circ\) nên \(\widehat {DAB} \ne \widehat {BAx}\)
\(\widehat {BCA} = \widehat {BDA}\) (hai góc nội tiếp cùng chắn cung \(AB\) )
Phương án A, B, D đúng
Cho tam giác $ABC$ nhọn nội tiếp đường tròn $\left( O \right)$ . $M$ là điểm thuộc cung nhỏ $AC$ (cung \(CM < \) cung \(AM\)). Vẽ $MH$ vuông góc với $BC$ tại $H$ , vẽ $MI$ vuông góc với $AC$ tại $I$ . Chọn câu đúng :
-
A.
$MIHC$ là hình chữ nhật.
-
B.
$MIHC$ là hình vuông.
-
C.
$MIHC$ không là tứ giác nội tiếp.
-
D.
$MIHC$ là tứ giác nội tiếp.
Đáp án : D
Tứ giác có 4 đỉnh thuộc một đường tròn thì nội tiếp đường tròn đó.
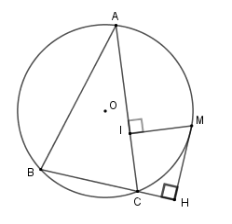
Tam giác MIC có $\widehat {MIC} = {90^0}$ ($MI$ vuông góc với $AC$) nên là tam giác vuông nội tiếp đường tròn đường kính MC.
Tam giác MHC có $\widehat {MHC} = {90^0}$ ($MH$ vuông góc với $BC$) nên là tam giác vuông nội tiếp đường tròn đường kính MC.
Suy ra tứ giác $IMHC$ nội tiếp (vì 4 đỉnh I, M, H, C cùng thuộc đường tròn đường kính BC) nên đáp án D đúng và đáp án C sai.
Tuy nhiên tứ giác $IMHC$ chưa đủ điều kiện để là hình chữ nhật và hình vuông nên đáp án A, B chưa chính xác.
Một ô tô đi quãng đường $AB$ với vận tốc $50\,\,km/h$ , rồi đi tiếp quãng đường $BC$ với vận tốc $45km/h.$ Biết quãng đường tổng cộng dài $165\,\,km$ và thời gian ô tô đi trên quãng đường $AB$ ít hơn thời gian đi trên quãng đường $BC$ là $30$ phút. Tính thời gian ô tô đi trên đoạn đường $AB$.
-
A.
$2$ giờ
-
B.
$1,5$ giờ
-
C.
$1$ giờ
-
D.
$3$ giờ
Đáp án : B
Gọi thời gian ô tô đi trên mỗi đoạn đường $AB$ và $BC$ lần lượt là $x,y$
($x>0;y>0,5$ ; đơn vị : giờ). Ta có hệ phương trình :
\(\left\{ \begin{array}{l}50.x + 45.y = 165\\y - x = 0,5\end{array} \right. \\ \left\{ \begin{array}{l}x = 1,5\\y = 2\end{array} (TM) \right.\)
Vậy thời gian ô tô đi hết quãng đường $AB$ là $1,5$ giờ. Thời gian ô tô đi hết quãng đường $BC$ là $2$ giờ.
Tâm đường tròn nội tiếp của tam giác là
-
A.
giao của ba đường phân giác góc trong tam giác
-
B.
giao ba đường trung trực của tam giác
-
C.
trọng tâm tam giác
-
D.
trực tâm tam giác
Đáp án : A
Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác các góc trong tam giác.
Cho tam giác \(ABC\) có \(BC\) cố định và góc \(A\) bằng \(50^\circ \). Gọi \(D\) là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm \(D\).
-
A.
Một cung chứa góc \(115^\circ \) dựng trên đoạn \(BC\).
-
B.
Một cung chứa góc \(115^\circ \) dựng trên đoạn \(AC\).
-
C.
Hai cung chứa góc \(115^\circ \) dựng trên đoạn \(AB\).
-
D.
Hai cung chứa góc \(115^\circ \) dựng trên đoạn \(BC\).
Đáp án : D
Sử dụng tính chất tia phân giác để tính góc \(BDC\) từ đó sử dụng quỹ tích cung chứa góc
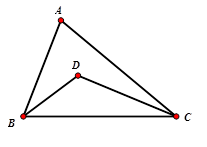
Ta có \(\widehat A = 50^\circ \Rightarrow \widehat B + \widehat C = 130^\circ \) nên \(\widehat {BDC} + \widehat {DBC} = \dfrac{{130^\circ }}{2} = 65^\circ \Rightarrow \widehat {BDC} = 115^\circ \)
Quỹ tích của điểm $D$ là hai cung chứa góc \(115^\circ \) dựng trên đoạn $BC$.
Giá trị của biểu thức \(2\sqrt {\dfrac{{16a}}{3}} - 3\sqrt {\dfrac{a}{{27}}} - 6\sqrt {\dfrac{{4a}}{{75}}} \) là
-
A.
$\dfrac{{23\sqrt {3a} }}{{15}}$
-
B.
$\dfrac{{\sqrt {3a} }}{{15}}$
-
C.
$\dfrac{{23\sqrt a }}{{15}}$
-
D.
$\dfrac{{3\sqrt {3a} }}{{15}}$
Đáp án : A
- Sử dụng công thức đưa thừa số ra ngoài dấu căn để xuất hiện nhân tử chung từ đó thực hiện phép tính
Công thức đưa thừa số ra ngoài dấu căn:
Với hai biểu thức $A,B$ mà $B \ge 0$, ta có $\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,{\rm{khi}}\,\,A \ge 0\\ - A\sqrt B \,{\rm{khi}}\,A < 0\end{array} \right.$
- Sử dụng công thức trục căn thức $\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{B},\,\left( {A \ge 0;\,B > 0} \right)$.
Ta có \(2\sqrt {\dfrac{{16a}}{3}} - 3\sqrt {\dfrac{a}{{27}}} - 6\sqrt {\dfrac{{4a}}{{75}}} = 2\sqrt {{4^2}.\dfrac{a}{3}} - 3\sqrt {\dfrac{1}{9}.\dfrac{a}{3}} - 6\sqrt {\dfrac{4}{{25}}.\dfrac{a}{3}} \)$ = 2.4\sqrt {\dfrac{a}{3}} - 3.\dfrac{1}{3}\sqrt {\dfrac{a}{3}} - 6.\dfrac{2}{5}.\sqrt {\dfrac{a}{3}} $
$ = \sqrt {\dfrac{a}{3}} .\left( {8 - 1 - \dfrac{{12}}{5}} \right) = \dfrac{{23}}{5}\sqrt {\dfrac{a}{3}} = \dfrac{{23}}{5}.\dfrac{{\sqrt {3a} }}{3} = \dfrac{{23\sqrt {3a} }}{{15}}$
Rút gọn biểu thức: $A = \left( {\dfrac{{\sqrt x }}{2} - \dfrac{1}{{2\sqrt x }}} \right)\left( {\dfrac{{x - \sqrt x }}{{\sqrt x + 1}} - \dfrac{{x + \sqrt x }}{{\sqrt x - 1}}} \right)$ v ới \(x > 0;\,\,x \ne 1.\)
-
A.
\(A = - 2\sqrt x \)
-
B.
\(A = 2\sqrt x \)
-
C.
\(A = - \sqrt x \)
-
D.
\(A = 4\sqrt x \)
Đáp án : A
+ Phân tích mẫu thức thành nhân tử rồi qui đồng mẫu các phân thức
+ Từ đó rút gọn phân thức
$\begin{array}{l}A = \left( {\dfrac{{\sqrt x }}{2} - \dfrac{1}{{2\sqrt x }}} \right)\left( {\dfrac{{x - \sqrt x }}{{\sqrt x + 1}} - \dfrac{{x + \sqrt x }}{{\sqrt x - 1}}} \right) = \dfrac{{x - 1}}{{2\sqrt x }}.\left( {\dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x + 1}} - \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x - 1}}} \right)\\\,\,\,\,\,\, = \dfrac{{x - 1}}{{2\sqrt x }}.\dfrac{{\sqrt x {{\left( {\sqrt x - 1} \right)}^2} - \sqrt x {{\left( {\sqrt x + 1} \right)}^2}}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} = \dfrac{{x - 1}}{{2\sqrt x }}.\dfrac{{\sqrt x \left[ {x - 2\sqrt x + 1 - \left( {x + 2\sqrt x + 1} \right)} \right]}}{{x - 1}}\\\,\,\,\,\,\, = \dfrac{{x - 2\sqrt x + 1 - x - 2\sqrt x - 1}}{2} = \dfrac{{ - 4\sqrt x }}{2} = - 2\sqrt x .\end{array}$
Vậy \(A = - 2\sqrt x \) với \(x > 0;\,\,x \ne 1.\)
Giải phương trình \(\sqrt {2{x^2} - 4x + 5} = x - 2\) ta được nghiệm là
-
A.
\(x = 1\)
-
B.
\(x = 3\)
-
C.
\(x = 2\)
-
D.
Phương trình vô nghiệm
Đáp án : D
+ Tìm điều kiện
+ Giải phương trình dạng \(\sqrt A = B\,\left( {B \ge 0} \right) \Leftrightarrow A = {B^2}\)
Điều kiện:
\(x - 2 \ge 0 \Leftrightarrow x \ge 2.\)
Ta có: \(\sqrt {2{x^2} - 4x + 5} = x - 2\)\( \Leftrightarrow 2{x^2} - 4x + 5 = {\left( {x - 2} \right)^2}\)
\( \Leftrightarrow 2{x^2} - 4x + 5 = {x^2} - 4x + 4 \Leftrightarrow {x^2} + 1 = 0\) \( \Leftrightarrow {x^2} = - 1\,\) (vô nghiệm vì \({x^2} \ge 0\,\,\forall x\) )
Vậy phương trình vô nghiệm.
Với giá trị nào của m thì đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung?
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = - 1$
-
D.
$m = 2$
Đáp án : A
Để hai đường thẳng ${d_1}:y = ax + b$ và ${d_2}:y = a'x + b'$ cắt nhau tại một điểm trên trục tung thì $\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$
Để hai đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung thì
$\left\{ \begin{array}{l} - 2 \ne 5\\m + 2 = 5 - 2m\end{array} \right.$$ \Leftrightarrow 3m = 3 \Leftrightarrow m = 1$.
Cho đường thẳng $d:y = 3x - \dfrac{1}{2}$. Giao điểm của $d$ với trục tung là
-
A.
$A\left( {\dfrac{1}{6};0} \right)$
-
B.
$B\left( {0;\dfrac{1}{2}} \right)$
-
C.
$C\left( {0;\dfrac{{ - 1}}{6}} \right)$
-
D.
$D\left( {0; - \dfrac{1}{2}} \right)$
Đáp án : D
Tìm tọa độ giao điểm của hai đường thẳng theo các bước
Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.
Giao điểm của đường thẳng $d$ và trục tung có hoành độ $x = 0$. Thay $x = 0$ vào phương trình $y = 3x - \dfrac{1}{2}$ ta được $y = 3.0 - \dfrac{1}{2} = - \dfrac{1}{2}$.
Vậy tọa độ giao điểm cần tìm là $D\left( {0; - \dfrac{1}{2}} \right)$
Cho hai đường thẳng $d:y = \left( {m + 2} \right)x - m$ và $d':y = - 2x - 2m + 1$ .Với giá trị nào của $m$ thì $d \equiv d'$?
-
A.
$m = - 2$
-
B.
$m = - 4$
-
C.
$m = 2$
-
D.
Không có $m$ thỏa mãn
Đáp án : D
Sử dụng vị trí tương đối giữa hai đường thẳng
Cho hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$.
+) $d{\rm{//}}d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$
+) \(d\) cắt $d'$\( \Leftrightarrow a \ne a'\).
+) \(d \equiv d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\).
+) \(d \bot d' \Leftrightarrow a.a' = - 1\).
+) Ta thấy $d:y = \left( {m + 2} \right)x - m$ có $a = m + 2$ và $d':y = - 2x - 2m + 1$ có $a' = - 2$ .
+) Điều kiện để $y = \left( {m + 2} \right)x - m$ là hàm số bậc nhất $m + 2 \ne 0 \Leftrightarrow m \ne - 2$
+) Để \(d\)$ \equiv $$d'$\( \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\)$ \Leftrightarrow \left\{ \begin{array}{l}m + 2 = - 2\\ - m = - 2m + 1\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}m = - 4\\m = 1\end{array} \right.$ (vô lý)
Vậy không có giá trị nào của $m$ để \(d\)$ \equiv $$d'$.
Cho hệ phương trình: $\left\{ \begin{array}{l}\left( {a + 1} \right)x - y = a + 1\begin{array}{*{20}{c}}{}&{\left( 1 \right)}\end{array}\\x + \left( {a - 1} \right)y = 2\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{}&{\left( 2 \right)}\end{array}}&{}\end{array}\end{array} \right.$
( $a$ là tham số)
Với $a \ne 0$ hệ có nghiệm duy nhất $\left( {x;y} \right)$. Tìm các số nguyên $a$ để hệ phương trình có nghiệm nguyên
-
A.
$a = 1$
-
B.
$a = - 1$
-
C.
$a \ne \left\{ { \pm 1} \right\}$
-
D.
$a = \pm 1$
Đáp án : D
Bước 1: Rút $x$ từ phương trình dưới thay vào phương trình trên
Bước 2: Tìm $y$ theo phương trình mới, từ đó suy ra $x$
Bước 3: Từ điều kiện $x,y$ nguyên để tìm $a$.
Từ PT $\left( 1 \right)$ ta có: $y = \left( {a + 1} \right)x - \left( {a + 1} \right)$ (*) thế vào PT $\left( 2 \right)$ ta được: $x + \left( {a - 1} \right)\left[ {\left( {a + 1} \right)x - \left( {a + 1} \right)} \right] = 2 \Leftrightarrow x + \left( {{a^2} - 1} \right)x - \left( {{a^2} - 1} \right) = 2 \Leftrightarrow {a^2}x = {a^2} + 1 \,\,\,\, (3)$
Với $a \ne 0$ , phương trình $\left( 3 \right)$ có nghiệm duy nhất $x = \dfrac{{{a^2} + 1}}{{{a^2}}}$ . Thay vào $\left( * \right)$ ta có:
$y = \left( {a + 1} \right)\dfrac{{{a^2} + 1}}{{{a^2}}} - \left( {a + 1} \right) = \dfrac{{\left( {a + 1} \right)\left( {{a^2} + 1} \right) - {a^2}\left( {a + 1} \right)}}{{{a^2}}} = \dfrac{{{a^3} + a + {a^2} + 1 - {a^3} - {a^2}}}{{{a^2}}} = \dfrac{{a + 1}}{{{a^2}}}$
Suy ra hệ phương trình đã cho có nghiệm duy nhất$\left( {x;y} \right) = \left( {\dfrac{{{a^2} + 1}}{{{a^2}}};\dfrac{{a + 1}}{{{a^2}}}} \right)$
Hệ phương trình có nghiệm nguyên: $\left\{ {\begin{array}{*{20}{c}}{x \in \mathbb{Z}}\\{y \in \mathbb{Z}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\dfrac{{{a^2} + 1}}{{{a^2}}} \in \mathbb{Z}}\\{\dfrac{{a + 1}}{{{a^2}}} \in \mathbb{Z}}\end{array}} \right.\begin{array}{*{20}{c}}{}&{\left( {a \in \mathbb{Z}} \right)}\end{array}$
Điều kiện cần: $x = \dfrac{{{a^2} + 1}}{{{a^2}}} = 1 + \dfrac{1}{{{a^2}}} \in \mathbb{Z}$
$\Leftrightarrow \dfrac{1}{{{a^2}}} \in \mathbb{Z} $ mà $a^2 > 0$
\( \Rightarrow {a^2} = 1 \Leftrightarrow a = \pm 1\) (TM \(a \ne 0\))
Điều kiện đủ:
$a = - 1 \Rightarrow y = 0 \in \mathbb{Z}$ (nhận)
$a = 1 \Rightarrow y = 2 \in \mathbb{Z}$ (nhận)
Vậy $a = \pm 1$ hệ phương trình đã cho có nghiệm nguyên.
Hai xí nghiệp theo kế hoạch phải làm tổng cộng $360$ dụng cụ. Trên thực tế, xí nghiệp $1$ vượt mức $12\% $ , xí nghiệp $2$ vượt mức $10\% $ , do đó cả hai xí nghiệp làm tổng cộng $400$ dụng cụ. Tính số dụng cụ xí nghiệp $2$ phải làm theo kế hoạch
-
A.
\(160\) dụng cụ
-
B.
\(200\) dụng cụ.
-
C.
\(120\) dụng cụ.
-
D.
\(240\) dụng cụ.
Đáp án : A
Gọi số dụng cụ cần làm của xí nghiệp $1$ và xí nghiệp $2$ lần lượt là : \(x,y\),
(\(x,y \in {N^*}\) \(x,y < 360\), dụng cụ).
Số dụng cụ xí nghiệp $1$ và xí nghiệp $2$ làm được khi vượt mức lần lượt là \(112\% x\) và \(110\% y\) ( dụng cụ).
Ta có hệ phương trình : \(\left\{ \begin{array}{l}x + y = 360\\112\% x + 110\% y = 400\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 200\\y = 160\end{array} \right.\).
Vậy xí nghiệp $1$ phải làm \(200\) dụng cụ, xí nghiệp $2$ phải làm \(160\) dụng cụ.
Hai giá sách có $450$ cuốn. Nếu chuyển $50$ cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên giá thứ hai bằng $\dfrac{4}{5}$ số sách ở giá thứ nhất. Tính số sách trên giá thứ hai.
-
A.
$150$ cuốn
-
B.
$300$ cuốn
-
C.
$200$ cuốn
-
D.
$250$ cuốn
Đáp án : A
Gọi số sách trên hai giá lần lượt là \(x,y\)
( \(0 < x,y < 450\), cuốn ).
Vì hai giá sách có $450$ cuốn nên ta có phương trình $x + y = 450$ (cuốn)
Nếu chuyển $50$ cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên giá thứ hai bằng $\dfrac{4}{5}$ số sách ở giá thứ nhất nên ta có phương trình $y + 50 = \dfrac{4}{5}\left( {x - 50} \right)$
Suy ra hệ phương trình : \(\left\{ \begin{array}{l}x + y = 450\\y + 50 = \dfrac{4}{5}\left( {x - 50} \right)\end{array} \right. \) hay \( \left\{ \begin{array}{l}x + y = 450\\\dfrac{4}{5}x - y = 90\end{array} \right. \)
Giải hệ phương trình, ta được \(\left\{ \begin{array}{l}x = 300\\y = 150\end{array} \right.\) (thỏa mãn)
Vậy số sách trên giá thứ nhất là \(300\) cuốn, số sách trên giá thứ hai là \(150\) cuốn.
Lập phương trình nhận hai số $3 - \sqrt 5 $ và $3 + \sqrt 5 $ làm nghiệm.
-
A.
${x^2} - 6x - 4 = 0$
-
B.
${x^2} - 6x + 4 = 0$
-
C.
${x^2} + 6x + 4 = 0$
-
D.
$ - {x^2} - 6x + 4 = 0$
Đáp án : B
Bước 1: Tìm tổng $S$ và tích $P$ của hai nghiệm.
Bước 2: Hai số đó là hai nghiệm của phương trình ${x^2} - Sx + P = 0$ (ĐK: ${S^2} - 4P \ge 0$)
Ta có $S = 3 - \sqrt 5 + 3 + \sqrt 5 = 6$ và $P = \left( {3 - \sqrt 5 } \right)\left( {3 + \sqrt 5 } \right) = 4$
Vì ${S^2} - 4P = 36 - 16 = 20 > 0$ nên hai số $3 - \sqrt 5 $ và $3 + \sqrt 5 $ là nghiệm của phương trình ${x^2} - 6x + 4 = 0$.
Tìm giá trị của \(m\) để phương trình \({x^2} + (4m + 1)x + 2(m - 4) = 0\) c ó hai nghiệm \({x_1},{x_2}\) và biểu thức \(A = {\left( {{x_1} - {x_2}} \right)^2}\) đạt giá trị nhỏ nhất.
-
A.
$m = 1$
-
B.
$m = 0$
-
C.
$m = 2$
-
D.
$m = 3$
Đáp án : B
Bước 1. Tìm điều kiện để phương trình có nghiệm \(\left\{ \begin{array}{l}a \ne 0\\\Delta \ge 0\end{array} \right.\).
Bước 2. Từ hệ thức đã cho và hệ thức Vi-ét, tìm được điều kiện của tham số.
Bước 3. Kiểm tra điều kiện của tham số xem có thỏa mãn điều kiện ở bước 1 hay không rồi kết luận.
Phương trình \({x^2} + (4m + 1)x + 2(m - 4) = 0\) có $a = 1 \ne 0$ và $\Delta = {\left( {4m + 1} \right)^2} - 8\left( {m - 4} \right) = 16{m^2} + 33 > 0;\forall m$
Nên phương trình luôn có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo hệ thức Vi-ét ta có $\left\{ \begin{array}{l}{x_1} + {x_2} = - 4m - 1\\{x_1}.{x_2} = 2m - 8\end{array} \right.$
Xét \(A = {\left( {{x_1} - {x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 16{m^2} + 33 \ge 33\)
Dấu “=” xảy ra khi $m = 0$
Vậy $m = 0$ là giá trị cần tìm.
Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt
-
A.
$m = 2$
-
B.
$m = - 2$
-
C.
$m = 4$
-
D.
$m \in \mathbb{R}$
Đáp án : D
Bước 1: Xét phương trình hoành độ giao điểm của đường thẳng và parabol
Bước 2: Để đường thẳng cắt parabol tại hai điểm phân biệt thì phương trình hoành độ giao điểm có hai nghiệm phân biệt.
Xét phương trình hoành độ giao điểm $\dfrac{{{x^2}}}{2} = mx + 2 \Leftrightarrow {x^2} - 2mx - 4 = 0$ có $\Delta ' = {m^2} + 4$
Vì $\Delta ' = {m^2} + 4 > 0;\forall m$ nên đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt với mọi $m$.
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai ?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Đáp án : D
Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.
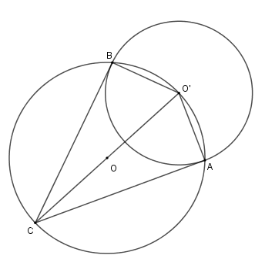
Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$.
Do đó $AB,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau)
Nên A, B, C đúng.
Cho hình vuông \(ABCD\). Trên cạnh \(BC\) lấy điểm \(E\) , trên tia đối của tia \(CD\) lấy điểm \(F\) sao cho \(CE = CF\). Gọi \(M\) là giao điểm của hai đường thẳng \(DE\) và \(BF\). Tìm quỹ tích của điểm \(M\) khi \(E\) di động trên cạnh \(BC\).
-
A.
Nửa đường tròn đường kính $BD$ .
-
B.
Cung \(BC\) của đường tròn đường kính $BD$.
-
C.
Cung \(BC\) của đường tròn đường kính $BD$ trừ điểm \(B,C\) .
-
D.
Đường tròn đường kính $BD$ .
Đáp án : B
Sử dụng : Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\).

Ta có \(\Delta DEC = \Delta BFC\left( {c - g - c} \right)\) \( \Rightarrow \widehat {EDC} = \widehat {EBM}\) \( \Rightarrow \widehat {EDC} + \widehat {DEC} = \widehat {EBM} + \widehat {BEM} \Rightarrow \widehat {EMB} = 90^\circ \)
Hay \(\widehat {BMD} = 90^\circ \) nên $M$ thuộc đườngtròn đường kính $BD$ . Mà \(E \in BC\) nên quỹ tích của điểm $M$ là cung \(BC\) của đường tròn đường kính $BD$ .
Cho tam giác $ABC$ vuông tại $A$ và điểm $D$ nằm giữa $A$ và $B$ . Đường tròn đường kính $BD$ cắt $BC$ tại $E$. Các đường thẳng $CD$ , $AE$ lần lượt cắt đường tròn tại các điểm thứ hai là $F$ và $G$. Khi đó, kết luận không đúng là:
-
A.
$\Delta ABC\backsim\Delta EBD$.
-
B.
Tứ giác $ADEC$ là tứ giác nội tiếp.
-
C.
Tứ giác $AFBC$ không là tứ giác nội tiếp.
-
D.
Các đường thẳng $AC,DE$ và $BF$ đồng quy.
Đáp án : C
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.
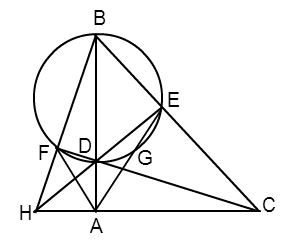
+) Xét đường tròn đường kính $BD$ có góc $BED$ là góc nội tiếp chắn nửa đường tròn nên \( \widehat {BED} = {90^0}.\)
Xét \(\Delta ABC\) và \(\Delta BED\) ta có: \(\widehat {DBE}\;\;chung\) và \(\widehat {BAC} = \widehat {BED} = {90^0}\) suy ra $\Delta ABC\backsim\Delta EBD\;\left( {g - g} \right)$
Vậy A đúng.
+) Do tam giác ADC vuông tại A (\(\widehat {DAC} = 90^0\)) và tam giác DEC vuông tại E (\(\widehat {DEC} = 90^0\)) nên tam giác ADC và tam giác DEC nội tiếp đường tròn đường kính DC.
Do đó tứ giác $ADEC$ là tứ giác nội tiếp. Vậy B đúng.
+) Chứng minh tương tự ta được tứ giác $AFBC$ là tứ giác nội tiếp. Vậy C sai.
+) Gọi giao điểm của $BF$ và $AC$ là $H$ .
Xét tam giác $BHC$ có hai đường cao $CF$ và $BA$ cắt nhau tại $D$. Do đó $D$ là trực tâm của tam giác $BHC$
Mà $DE = \bot AB$ nên $DE$ là đường cao của tam giác $BHC$ hay $H,E,D$ thẳng hàng.
Suy ra $DE,AC$ và $BF$ đồng quy tại $H$ suy ra D đúng.
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Đáp án : D
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
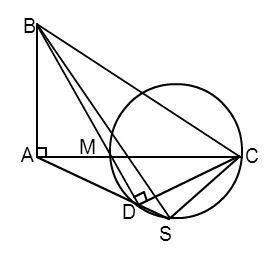
+) Ta có: \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn đường kính $MC$ \( \Rightarrow \widehat {MDC} = {90^0}\) (tính chất góc nội tiếp).
Xét tứ giác $ABCD$ ta có:
Góc $BAC$ và góc $BDC$ cùng nhìn đoạn $BC$ dưới góc \({90^0}.\)
\( \Rightarrow \) $ABCD$ là tứ giác nội tiếp (dhnb) \( \Rightarrow \) phương án A đúng.
+) Xét tứ giác $ABCD$ nội tiếp ta có\(\widehat {ABD} = \widehat {ACD}\) (cùng nhìn đoạn $AD$ )\( \Rightarrow \) phương án B đúng.
+) Xét đường tròn đường kính $MC$ ta có $4$ điểm $M,C,D,S$ cùng thuộc đường tròn.
\( \Rightarrow \) Tứ giác $MCSD$ là tứ giác nội tiếp.
\( \Rightarrow \widehat {ADM} = \widehat {SCM}\) (góc ngoài tại $1$ đỉnh bằng góc trong tại đỉnh đối diện). $\left( 1 \right)$
Vì tứ giác $ABCD$ nội tiếp (cmt) \( \Rightarrow \widehat {ACB} = \widehat {ADB}\) (cùng nhìn đoạn$AB$ ) $\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ \( \Rightarrow \widehat {BCA} = \widehat {ACS}\;\;\;\left( { = \widehat {ADB}} \right).\)
Hay $CA$ là phân giác của \(\widehat {SCB} \Rightarrow \) phương án C đúng.
+) Giả sử tứ giác $ABCS$ là tứ giác nội tiếp \( \Rightarrow \widehat {ASB} = \widehat {BCA}\) (hai góc cùng nhìn đoạn $AB$ ).
Mà \(\widehat {ACB} = \widehat {BDA};\;\;\;\widehat {BAD} \ne \widehat {BSA}\) (xét trong đường tròn đường kính $CM$ )
\( \Rightarrow \widehat {ASB} \ne \widehat {BCA} \Rightarrow \) tứ giác $ABCS$ không là tứ giác nội tiếp \( \Rightarrow \)phương án D sai.
Cho tam giác $ABC$ vuông tại $A$ , cạnh $AB = 5\,\,cm$ , \(\widehat B = {60^ \circ }\). Đường tròn tâm $I$ , đường kính $AB$ cắt $BC$ ở $D$ . Chọn khẳng định sai?
-
A.
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là $\dfrac{\pi }{6}\,\,\left( {cm} \right)$
-
B.
$AD \bot BC$
-
C.
$D$ thuộc đường tròn đường kính \(AC\)
-
D.
Độ dài cung nhỏ $BD$ của \(\left( I \right)\) là \(\dfrac{{5\pi }}{6}\,\,\left( {cm} \right)\)
Đáp án : A
+ Sử dụng góc nội tiếp chắn nửa đường tròn bằng \(90^\circ \)
+ Sử dụng công thức tính độ dài cung tròn:
Trên đường tròn bán kính$R$ , độ dài $l$ của một cung \(n^\circ \) được tính theo công thức \(l = \dfrac{{\pi Rn}}{{180}}\,\).
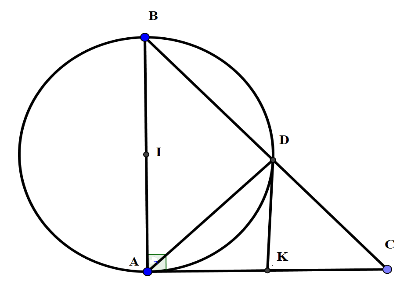
+ Xét đường tròn \(\left( I \right)\) đường kính \(AB\) có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên $AD \bot BC \Rightarrow $ phương án B đúng.
+) Gọi \(K\) là trung điểm của \(AC \Rightarrow KA = KC = KD \Rightarrow K\) đường tròn đường kính \(AC \Rightarrow \) phương án C đúng.
+) Ta có \(\Delta IBD\) cân tại \(I\) có \(\widehat B = 60^\circ \Rightarrow \Delta IBD\) đều nên \(\widehat {BID} = 60^\circ \)
Độ dài cung nhỏ \(BD\) của \(\left( I \right)\) là $l = \dfrac{{\pi .\dfrac{5}{2}.60}}{{180^\circ }} = \dfrac{{5\pi }}{6}\,\left( {cm} \right) \Rightarrow $ phương án D đúng.
Cho hình chữ nhật \(ABCD\) có \(AB = 4\,cm;AD = 3\,cm\) . Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) .
-
A.
\(25\pi \)
-
B.
\(\dfrac{{25\pi }}{8}\)
-
C.
\(25\)
-
D.
\(\dfrac{{25\pi }}{4}\)
Đáp án : A
Công thức diện tích mặt cầu $S = 4\pi {R^2}$
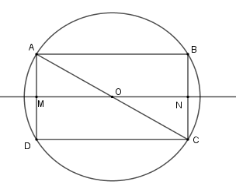
Gọi \(O\) là tâm của hình chữ nhật nên $OA = OB = OC = OD$ nên \(O\) là tâm đường tròn ngoại tiếp hình chữ nhật \(ABCD\) . Khi đó bán kính đường tròn là \(R = OA = \dfrac{{AC}}{2}\)
Áp dụng định lí Pythagore vào tam giác ADC, ta có:
\(A{C^2} = A{D^2} + D{C^2} = {3^2} + {4^2} = 25\)
suy ra \(AC = 5\) (vì \(AB = DC = 4\,cm\) )
Do đó \( R = \dfrac{5}{2}\)
Khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quay quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) ta được một hình cầu tâm \(O\) bán kính $R = \dfrac{5}{2}$
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4.\pi {\left( {\dfrac{5}{2}} \right)^2} = 25\pi \) \(\left( {cm} \right)\) .
Cho tam giác $ABC$ vuông tại $A$. Tính \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
-
A.
\(0\)
-
B.
\(1\)
-
C.
\( - 1\)
-
D.
\(2\)
Đáp án : A
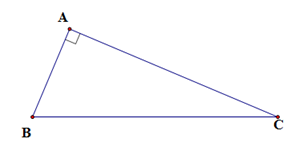
Ta có: \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}}\)
\(\sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\;\)
\(\tan B = \dfrac{{AC}}{{AB}} \); \( \tan C = \dfrac{{AB}}{{AC}}\)
Vậy \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\;\)
\( = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1\)
\( = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0\) (vì theo định lý Pytago thì \(A{C^2} + A{B^2} = B{C^2}\) )
Cho đoạn thẳng $AB = 2a$ và trung điểm $O$ của nó. Trên nửa mặt phẳng bờ $AB$ vẽ các tia $Ax,By\;$ vuông góc với $AB.$ Qua \(O\) vẽ một tia cắt tia \(Ax\) tại $M$ sao cho $\widehat {AOM} = \alpha < {90^0}$ . Qua $O$ vẽ tia thứ hai cắt tia $By$ tại $N$ sao cho \(\widehat {MON} = 90^\circ \) . Khi đó, diện tích tam giác \(MON\) là
-
A.
\(\dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
-
B.
\(\dfrac{{{a^2}}}{{\sin \alpha .\cos \alpha }}\)
-
C.
\(\dfrac{a}{{2\sin \alpha .\cos \alpha }}\)
-
D.
\(\dfrac{{2{a^2}}}{{\sin \alpha .\cos \alpha }}\)
Đáp án : A
Áp dụng hệ thức về cạnh và góc trong tam giác vuông
Áp dụng công thức tính diện tích tam giác vuông
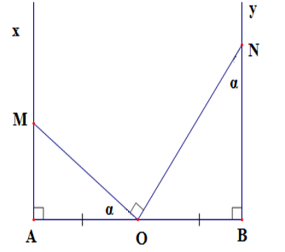
Theo đề bài ta có: \(AB = 2a \Rightarrow OA = OB = a\)
Ta có: \(\widehat {ONB} = \widehat {AOM} = \alpha \) (cùng phụ với \(\widehat {BON}\) )
Xét \(\Delta AOM\) có \(\widehat A = 90^\circ \) Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OA = OM.\cos \alpha \Rightarrow OM = \dfrac{a}{{\cos \alpha }}\) Xét \(\Delta BON\) có \(\widehat B = 90^\circ \) Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OB = ON.\sin \alpha \Rightarrow ON = \dfrac{a}{{\sin \alpha }}\) Vậy diện tích tam giác \(MON\) là: \(\dfrac{1}{2}OM.ON = \dfrac{1}{2}.\dfrac{a}{{\cos \alpha }}.\dfrac{a}{{\sin \alpha }} = \dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)