Đề kiểm tra học kì 2 Toán 9 - Đề số 2
Đề bài
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
-
A.
Số đo cung lớn
-
B.
Số đo của góc ở tâm chắn cung đó
-
C.
Số đo của góc ở tâm chắn cung lớn
-
D.
Số đo của cung nửa đường tròn
Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung?
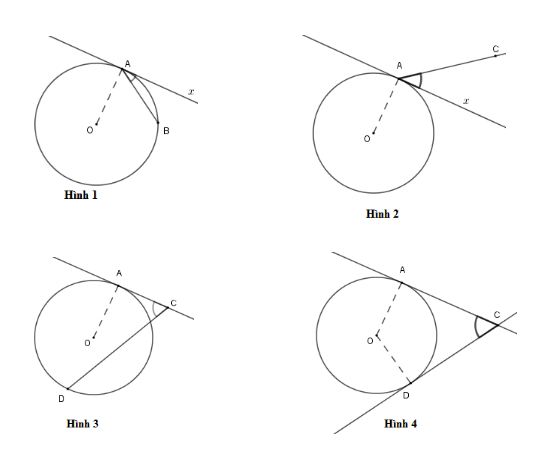
-
A.
Hình $1$
-
B.
Hình $2$
-
C.
Hình $3$
-
D.
Hình $4$
Chọn khẳng định đúng.
-
A.
Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
B.
Trong một đường tròn, đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
C.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì song song với dây căng cung ấy
-
D.
Trong một đường tròn, hai đường kính luôn vuông góc với nhau
Cho hệ phương trình \(\left\{ \begin{array}{l}2x - 3y = 1\\4x + y = 9\end{array} \right.\) . Nghiệm của hệ phương trình là $\left( {x;y} \right)$ , tính $x - y$
-
A.
$x - y = - 1$
-
B.
$x - y = 1$
-
C.
$x - y = 0$
-
D.
$x - y = 2$
Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là
-
A.
$AB = 8,6\,cm$
-
B.
$AB = 6,9\,cm$
-
C.
$AB = 4,8\,cm$
-
D.
$AB = 9,6\,cm$
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |
-
A.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
B.
$\left( 1 \right)$ : $9\,cm$; $\left( 2 \right)$ : cắt nhau
-
C.
$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
D.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $6\,cm$
Cho hai đường thẳng $d:y = x + 3$ và $d':y = - 2x$. Khi đó
-
A.
$d{\rm{//}}d'$
-
B.
$d \equiv d'$
-
C.
$d$ cắt $d'$
-
D.
\(d \bot d'\)
Giá trị của biểu thức \(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \) là
-
A.
$1$
-
B.
$0$
-
C.
$2$
-
D.
$3$
Đưa thừa số $\sqrt {81{{\left( {2 - y} \right)}^4}} $ ra ngoài dấu căn ta được ?
-
A.
$9\left( {2 - y} \right)$
-
B.
$81{\left( {2 - y} \right)^2}$
-
C.
$9{\left( {2 - y} \right)^2}$
-
D.
$ - 9{\left( {2 - y} \right)^2}$
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Chọn khẳng định sai ?
-
A.
\(b = a.\sin B = a.\cos C\)
-
B.
$a = c.\tan B = c.\cot C$
-
C.
${a^2} = {b^2} + {c^2}$
-
D.
\(c = a.\sin C = a.\cos B\)
Số đường tròn nội tiếp của một đa giác đều là
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(0\)
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 12cm\) và đường kính đáy là \(d= 8\,cm\) . Tính diện tích các mặt của hộp sữa. Lấy \(\pi \approx 3,14\)
-
A.
\(110\pi \,\left( {c{m^2}} \right)\)
-
B.
\(128\pi \,\left( {c{m^2}} \right)\)
-
C.
\(96\pi \,\left( {c{m^2}} \right)\)
-
D.
\(112\pi \,\left( {c{m^2}} \right)\)
Cho đường thẳng $d:$ $y = \left( {m + 2} \right)x - 5$ đi qua điểm $A\left( { - 1;2} \right)$ . Hệ số góc của đường thẳng $d$ là
-
A.
$1$
-
B.
$11$
-
C.
$ -7$
-
D.
$7$
Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng ?
-
A.
$MN = MP.\sin P$
-
B.
$MN = MP.\cos P$
-
C.
$MN = MP.\tan P$
-
D.
$MN = MP.\cot P$
Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:
-
A.
$2$
-
B.
$1$
-
C.
$0$
-
D.
$3$
Tìm $m$ để phương trình $2m{x^2} - \left( {2m + 1} \right)x - 3 = 0$ có nghiệm là $x = 2$.
-
A.
$m = - \dfrac{5}{4}$
-
B.
$m = \dfrac{1}{4}$
-
C.
$m = \dfrac{5}{4}$
-
D.
$m = - \dfrac{1}{4}$
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
-
A.
$40^\circ $
-
B.
$45^\circ $
-
C.
$60^\circ $
-
D.
$30^\circ $
Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình ${x^2} - 6x + 7 = 0$
-
A.
$\dfrac{1}{6}$
-
B.
$3$
-
C.
$6$
-
D.
$7$
Rút gọn biểu thức \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \) với $a \ge 0;b \ge 0$ ta được kết quả là
-
A.
$2\sqrt {2a} $
-
B.
$4\sqrt a $
-
C.
$8\sqrt a $
-
D.
$2\sqrt a $
Rút gọn biểu thức \(2\sqrt a - \sqrt {9{a^3}} + {a^2}\sqrt {\dfrac{{16}}{a}} + \dfrac{2}{{{a^2}}}\sqrt {36{a^5}} \) với $a > 0$ ta được
-
A.
$14\sqrt a + a\sqrt a $
-
B.
$14\sqrt a - a\sqrt a $
-
C.
$14\sqrt a + 2a\sqrt a $
-
D.
$20\sqrt a - 2a\sqrt a $
Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng $d:y = \left( {m + 2} \right)x - m$ và $d':y = - 2x - 2m + 1$. Với giá trị nào của $m$ thì $d$ cắt $d'$?
-
A.
$m \ne - 2$
-
B.
$m \ne - 4$
-
C.
$m \ne \left\{ { - 2; - 4} \right\}$
-
D.
$m \ne \left\{ {2; - 4} \right\}$
Cho hệ phương trình $\left\{ \begin{array}{l}2x + by = - 1\\bx - 2ay = 1\end{array} \right.$. Biết rằng hệ phương trình có nghiệm là $\left( {1; - 2} \right)$, tính $a - b$.
-
A.
$\dfrac{{13}}{8}$
-
B.
$ - \dfrac{{13}}{8}$
-
C.
$\dfrac{5}{8}$
-
D.
$ - \dfrac{5}{8}$
Cho hệ phương trình $\left\{ \begin{array}{l}(m - 1)x + y = 2\\mx + y = m + 1\end{array} \right.$ ( $m$ là tham số) . Kết luận nào sau đây là đúng khi nói về nghiệm $\left( {x;y} \right)$ của hệ phương trình
-
A.
Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y \le {\rm{3}}$
-
B.
Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y > {\rm{3}}$
-
C.
Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y \ge {\rm{3}}$
-
D.
Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y = {\rm{3}}$
Một mảnh đất hình chữ nhật có chu vi bằng $42$ m. Đường chéo hình chữ nhật dài $15$ m. Tính độ dài chiều rộng mảnh đất hình chữ nhật.
-
A.
$10\,\,m$
-
B.
$12\,\,m$
-
C.
$9\,\,m$
-
D.
$8\,\,m$
Một canô chạy trên sông trong $7$ giờ, xuôi dòng \(108\,km\) và ngược dòng \(63\,km\) . Một lần khác cũng trong 7 giờ canô xuôi dòng \(81\,km\) và ngược dòng \(84\,km\) . Tính vận tốc nước chảy.
-
A.
$4\,{\rm{km/h}}$
-
B.
$3\,{\rm{km/h}}$
-
C.
$2\,{\rm{km/h}}$
-
D.
$2,5\,{\rm{km/h}}$
Cho phương trình \(\left( {m - 3} \right){x^2} - 2mx + m - 6 = 0\). Tìm các giá trị của $m$ để phương trình vô nghiệm
-
A.
$m < - 2$
-
B.
$m < 2$
-
C.
$m < 3$
-
D.
$m < - 3$
Tìm các giá trị của \(m\) để phương trình \({x^2} - 2\left( {m - 3} \right)x + 8 - 4m = 0\) có hai nghiệm âm phân biệt.
-
A.
$m < 2$ và $m \ne 1$
-
B.
$m < 3$
-
C.
$m <2$
-
D.
$m > 0$
Biết rằng phương trình $\left( {m - 2} \right){x^2} - \left( {2m + 5} \right)x + m + 7 = 0\,\left( {m \ne 2} \right)$ luôn có nghiệm ${x_1};{x_2}$ với mọi $m$. Tìm ${x_1};{x_2}$ theo $m$.
-
A.
${x_1} = - 1;{x_2} = - \dfrac{{m + 7}}{{m - 2}}$
-
B.
${x_1} = 1;{x_2} = - \dfrac{{m + 7}}{{m - 2}}$
-
C.
${x_1} = 1;{x_2} = \dfrac{{m + 7}}{{m - 2}}$
-
D.
${x_1} = - 1;{x_2} = \dfrac{{m + 7}}{{m - 2}}$
Số nghiệm của phương trình \(3{x^3} + 3{x^2} + 5x + 5 = 0\) là:
-
A.
$2$
-
B.
$0$
-
C.
$1$
-
D.
$3$
Một ca nô chạy xuôi dòng với quãng đường $42{\rm{km}}$, rồi sau đó ngược dòng trở lại $20{\rm{ km}}$ hết tổng cộng $5{\rm{h}}$. Biến vận tốc của dòng nước chảy là $2{\rm{ km/h}}$. Tính vận tốc của ca nô lúc dòng nước yên lặng.
-
A.
$11{\rm{ }}\left( {{\rm{km/h}}} \right)$
-
B.
$12{\rm{ }}\left( {{\rm{km/h}}} \right)$
-
C.
$14{\rm{ }}\left( {{\rm{km/h}}} \right)$
-
D.
$15{\rm{ }}\left( {{\rm{km/h}}} \right)$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
-
A.
$DE$ là cát tuyến của đường tròn đường kính $BH$
-
B.
$DE$ là tiếp tuyến của đường tròn đường kính $BH$
-
C.
Tứ giác$AEHD$ là hình chữ nhật
-
D.
$DE \bot DI$ (với $I$ là trung điểm $BH$)
Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
-
A.
$18\,cm$
-
B.
$6\sqrt 3 cm$
-
C.
$12\sqrt 3 \,cm$
-
D.
$15\,cm$
Cho hai đường tròn $\left( {O;20cm} \right)$ và $\left( {O';15cm} \right)$ cắt nhau tại $A$ và$B$. Tính đoạn nối tâm $OO'$, biết rằng$AB = 24cm$ và $O$ và $O'$ nằm cùng phía đối với $AB$ .
-
A.
$OO' = 7cm$
-
B.
$OO' = 8cm$
-
C.
$OO' = 9cm$
-
D.
$OO' = 25cm$
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
-
A.
\(AD.AE\)
-
B.
\(AD.AC\)
-
C.
\(AE.BE\)
-
D.
\(AD.BD\)
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
-
A.
\(A{B^2}\)
-
B.
\(B{C^2}\)
-
C.
\(A{C^2}\)
-
D.
\(A{M^2}\)
Cho đường tròn $\left( O \right)$ đường kính $AB$. Gọi $I$ là trung điểm của $OA$ . Dây $CD$ vuông góc với $AB$ tại $I$. Lấy $K$ tùy ý trên cung $BC$ nhỏ, $AK$ cắt $CD$ tại $H$. Khẳng định nào đúng ?
-
A.
Tứ giác $BIHK$ nội tiếp.
-
B.
Tứ giác $BIHK$ không nội tiếp.
-
C.
Tứ giác $BIHK$ là hình chữ nhật.
-
D.
Các đáp án trên đều sai.
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Cho tam giác đều \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \). Diện tích của tam giác đều \(ABC\) là:
-
A.
\(27\sqrt 3 \) $cm^2$
-
B.
\(7\sqrt 3 \) $cm^2$
-
C.
\(29\sqrt 3 \) $cm^2$
-
D.
\(9\sqrt 3 \) $cm^2$
Lời giải và đáp án
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
-
A.
Số đo cung lớn
-
B.
Số đo của góc ở tâm chắn cung đó
-
C.
Số đo của góc ở tâm chắn cung lớn
-
D.
Số đo của cung nửa đường tròn
Đáp án : B
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung?

-
A.
Hình $1$
-
B.
Hình $2$
-
C.
Hình $3$
-
D.
Hình $4$
Đáp án : A
Cho đường tròn tâm \((O)\) có \(Ax\) là tia tiếp tuyến tại tiếp điểm $A$ và dây cung $AB.$ Khi đó, góc \(BAx\)là góc tạo bởi tia tiếp tuyến và dây cung.
Chọn khẳng định đúng.
-
A.
Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
B.
Trong một đường tròn, đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
C.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì song song với dây căng cung ấy
-
D.
Trong một đường tròn, hai đường kính luôn vuông góc với nhau
Đáp án : A
+) Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
+) Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
+) Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
Cho hệ phương trình \(\left\{ \begin{array}{l}2x - 3y = 1\\4x + y = 9\end{array} \right.\) . Nghiệm của hệ phương trình là $\left( {x;y} \right)$ , tính $x - y$
-
A.
$x - y = - 1$
-
B.
$x - y = 1$
-
C.
$x - y = 0$
-
D.
$x - y = 2$
Đáp án : B
Nhân cả hai vế của phương trình thứ nhất với 3 để được phương trình mới có hệ số của biến đối nhau.
Sử dụng phương pháp cộng đại số để tìm nghiệm của hệ.
Ta có
\(\left\{ \begin{array}{l}2x - 3y = 1\\4x + y = 9\end{array} \right. \)
$\left\{ \begin{array}{l}2x - 3y = 1\\12x + 3y = 27\end{array} \right.$
$\left\{\begin{array}{l}2x - 3y = 1\\2x - 3y+12x+3y =1+ 27\end{array} \right.$
$\left\{ \begin{array}{l}2x - 3y = 1\\14x = 28\end{array} \right. $
\(\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)
Vậy hệ đã cho có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;1} \right)\)
$ \Rightarrow x - y = 2 - 1 = 1$ .
Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là
-
A.
$AB = 8,6\,cm$
-
B.
$AB = 6,9\,cm$
-
C.
$AB = 4,8\,cm$
-
D.
$AB = 9,6\,cm$
Đáp án : D
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông.
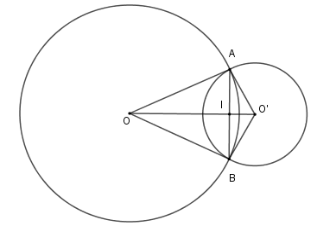
Vì $OA$ là tiếp tuyến của $\left( {O'} \right)$ nên $\Delta OAO'$ vuông tại $A$.
Vì $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A,B$ nên đường nối tâm $OO'$ là trung trực của đoạn $AB$.
Gọi giao điểm của $AB$ và $OO'$ là $I$ thì $AB \bot OO'$ tại $I$ là trung điểm của $AB$
Áp dụng hệ thức lượng trong tam giác vuông $OAO'$ ta có
$\dfrac{1}{{A{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O'{A^2}}} = \dfrac{1}{{{8^2}}} + \dfrac{1}{{{6^2}}} \Rightarrow AI = 4,8\,cm \Rightarrow AB = 9,6\,cm$
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |
-
A.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
B.
$\left( 1 \right)$ : $9\,cm$; $\left( 2 \right)$ : cắt nhau
-
C.
$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
D.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $6\,cm$
Đáp án : A
Sử dụng bảng vị trí tương đối của đường thẳng và đường tròn
|
Vị trí tương đối của đường thẳng và đường tròn |
Số điểm chung |
Hệ thức giữa $d$ và $R$ |
|
Đường thẳng và đường tròn cắt nhau |
$2$ |
$d < R$ |
|
Đường thẳng và đường tròn tiếp xúc nhau |
$1$ |
$d = R$ |
|
Đường thẳng và đường tròn không giao nhau |
$0$ |
$d > R$ |
+) Vì $d < R\left( {4cm < 5cm} \right)$ nên đường thẳng cắt đường tròn
+) Vì đường thẳng tiếp xúc với đường tròn nên $d = R = 8\,cm$
Cho hai đường thẳng $d:y = x + 3$ và $d':y = - 2x$. Khi đó
-
A.
$d{\rm{//}}d'$
-
B.
$d \equiv d'$
-
C.
$d$ cắt $d'$
-
D.
\(d \bot d'\)
Đáp án : C
Sử dụng vị trí tương đối giữa hai đường thẳng
Cho hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$.
+) $d{\rm{//}}d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$
+) \(d\)cắt$d'$\( \Leftrightarrow a \ne a'\).
+) \(d \equiv d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\).
+) \(d \bot d' \Leftrightarrow a.a' = - 1\).
Ta thấy $d:y = x + 3$ có $a = 1$ và $d':y = - 2x$ có $a' = - 2$$ \Rightarrow a \ne a'\left( {1 \ne - 2} \right)$ nên $d$ cắt $d'$.
Giá trị của biểu thức \(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \) là
-
A.
$1$
-
B.
$0$
-
C.
$2$
-
D.
$3$
Đáp án : B
-Sử dụng công thức khai phương một tích \(\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)\) đưa biểu thức về các căn thức cùng loại (cùng biểu thức dưới dấu căn).
-Cộng trừ các căn thức
\(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \)\( = \sqrt {16.2} + \sqrt {25.2} - 3\sqrt {4.2} - \sqrt {9.2} \)
\(= 4\sqrt 2 + 5\sqrt 2 - 6\sqrt 2 - 3\sqrt 2 = 0\)
Đưa thừa số $\sqrt {81{{\left( {2 - y} \right)}^4}} $ ra ngoài dấu căn ta được ?
-
A.
$9\left( {2 - y} \right)$
-
B.
$81{\left( {2 - y} \right)^2}$
-
C.
$9{\left( {2 - y} \right)^2}$
-
D.
$ - 9{\left( {2 - y} \right)^2}$
Đáp án : C
Sử dụng công thức đưa thừa số ra ngoài dấu căn: Với hai biểu thức $A,B$ mà $B \ge 0$, ta có $\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,{\rm{khi}}\,\,A \ge 0\\ - A\sqrt B \,{\rm{khi}}\,A < 0\end{array} \right.$
Ta có $\sqrt {81{{\left( {2 - y} \right)}^4}} = \sqrt {81.{{\left[ {{{\left( {2 - y} \right)}^2}} \right]}^2}} = \left| {{{\left( {2 - y} \right)}^2}} \right|\sqrt {81} = 9{\left( {2 - y} \right)^2}$
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Chọn khẳng định sai ?
-
A.
\(b = a.\sin B = a.\cos C\)
-
B.
$a = c.\tan B = c.\cot C$
-
C.
${a^2} = {b^2} + {c^2}$
-
D.
\(c = a.\sin C = a.\cos B\)
Đáp án : B
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,AC = b,AB = c.\) Ta có :
+) Theo định lý Py-ta-go ta có ${a^2} = {b^2} + {c^2}$ nên C đúng
+) Theo hệ thức về cạnh và góc trong tam giác vuông ta có
\(b = a.\sin B = a.\cos C\); \(c = a.\sin C = a.\cos B\); \(b = c.\tan B = c.\cot C\); \(c = b.\tan C = b.\cot B\).
Nên A,D đúng.
Số đường tròn nội tiếp của một đa giác đều là
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(0\)
Đáp án : A
Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 12cm\) và đường kính đáy là \(d= 8\,cm\) . Tính diện tích các mặt của hộp sữa. Lấy \(\pi \approx 3,14\)
-
A.
\(110\pi \,\left( {c{m^2}} \right)\)
-
B.
\(128\pi \,\left( {c{m^2}} \right)\)
-
C.
\(96\pi \,\left( {c{m^2}} \right)\)
-
D.
\(112\pi \,\left( {c{m^2}} \right)\)
Đáp án : D
Sử dụng công thức tính diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ và diện tích một đáy ${S_d} = \pi {R^2}.$
Bán kính đường tròn đáy \(R = \dfrac{8}{2} = 4\,cm\) nên diện tích một đáy ${S_d} = \pi {R^2} = 16\pi \,(c{m^2})$
Ta có diện tích xung quanh của hình trụ: ${S_{xq}} = 2\pi Rh = 2\pi .4.12 = 96\pi \,(c{m^2})$
Vì hộp sữa đã mất nắp nên diện tích các mặt của hộp sữa là:
\(96\pi + 16\pi = 112\pi \,\left( {c{m^2}} \right).\)
Cho đường thẳng $d:$ $y = \left( {m + 2} \right)x - 5$ đi qua điểm $A\left( { - 1;2} \right)$ . Hệ số góc của đường thẳng $d$ là
-
A.
$1$
-
B.
$11$
-
C.
$ -7$
-
D.
$7$
Đáp án : C
Bước 1: Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ để tìm $m$ và đưa phương trình về dạng $y = ax + b$ .
Bước 2: Sử dụng lý thuyết về hệ số góc của đường thẳng.
Đường thẳng $d$ có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) có $a$ là hệ số góc.
Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ ta được $\left( {m + 2} \right).\left( { - 1} \right) - 5 = 2 \Leftrightarrow -m-2=7\Leftrightarrow m = -9$
Suy ra $d:y = -7x - 5$
Hệ số góc của đường thẳng $d$ là $k = -7$ .
Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng ?
-
A.
$MN = MP.\sin P$
-
B.
$MN = MP.\cos P$
-
C.
$MN = MP.\tan P$
-
D.
$MN = MP.\cot P$
Đáp án : A
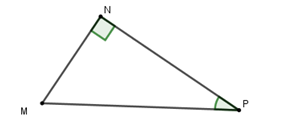
Ta có $\sin P = \dfrac{{MN}}{{MP}} \Rightarrow MN = MP.\sin P$.
Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:
-
A.
$2$
-
B.
$1$
-
C.
$0$
-
D.
$3$
Đáp án : A
Bước 1: Giải phương trình hoành độ giao điểm.
Bước 2: Số nghiệm vừa tìm được của phương trình là số giao điểm của đường thẳng và parabol
Xét phương trình hoành độ giao điểm ${x^2} = 2x + 4 \Leftrightarrow {x^2} - 2x - 4 = 0$ có $\Delta ' = 5 > 0$ nên phương trình có hai nghiệm phân biệt hay đường thẳng cắt parabol tại hai điểm phân biệt.
Tìm $m$ để phương trình $2m{x^2} - \left( {2m + 1} \right)x - 3 = 0$ có nghiệm là $x = 2$.
-
A.
$m = - \dfrac{5}{4}$
-
B.
$m = \dfrac{1}{4}$
-
C.
$m = \dfrac{5}{4}$
-
D.
$m = - \dfrac{1}{4}$
Đáp án : C
Thay $x = {x_0}$ vào phương trình đã cho ta được phương trình ẩn $m$. Giải phương trình ta tìm được $m$.
Thay $x = 2$ vào phương trình $2m{x^2} - \left( {2m + 1} \right)x - 3 = 0$ ta được:
$2m{.2^2} - \left( {2m + 1} \right).2 - 3 = 0 $
$ 4m - 5 = 0$
$m = \dfrac{5}{4}$
Vậy $m = \dfrac{5}{4}$ là giá trị cần tìm.
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
-
A.
$40^\circ $
-
B.
$45^\circ $
-
C.
$60^\circ $
-
D.
$30^\circ $
Đáp án : D
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
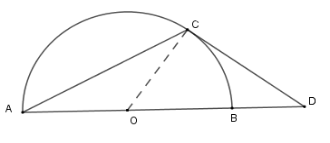
Xét nửa \(\left( O \right)\) có \(\widehat {BAC} = \dfrac{1}{2}\) sđ \(\overparen{BC}\) (góc nội tiếp chắn cung BC) và \(\widehat {CDA} = \dfrac{1}{2}\) (sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\) ) (góc có đỉnh bên ngoài đường tròn)
Mà \(\Delta ADC\) cân tại \(C\) nên \(\widehat {DAC} = \widehat {CDA} \Leftrightarrow \) sđ \(\overparen{BC} = \) sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\)
Suy ra sđ \(\overparen{AC} = 2\). sđ \(\overparen{BC}\)
Mà sđ \(\overparen{AC} + \) sđ \(\overparen{BC} = 180^\circ \) nên sđ \(\overparen{AC} = 120^\circ \) ; sđ\(\overparen{BC}= 60^\circ \)
Do đó $\widehat {ADC} = 30^\circ $.
Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình ${x^2} - 6x + 7 = 0$
-
A.
$\dfrac{1}{6}$
-
B.
$3$
-
C.
$6$
-
D.
$7$
Đáp án : C
Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình $a{x^2} + bx + c = 0\,\,(a \ne 0)$ thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1} \cdot {x_2} = \dfrac{c}{a}\end{array} \right..\)
Phương trình ${x^2} - 6x + 7 = 0$ có $\Delta = {\left( { - 6} \right)^2} - 4.1.7 = 8 > 0$ nên phương trình có hai nghiệm ${x_1};{x_2}$
Theo định lí Viète, ta có ${x_1} + {x_2} = - \dfrac{{ - 6}}{1} = 6$
Rút gọn biểu thức \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \) với $a \ge 0;b \ge 0$ ta được kết quả là
-
A.
$2\sqrt {2a} $
-
B.
$4\sqrt a $
-
C.
$8\sqrt a $
-
D.
$2\sqrt a $
Đáp án : D
Sử dụng công thức đưa thừa số vào trong dấu căn và công thức khai phương một tích để xuất hiện nhân tử chung từ đó thực hiện phép tính.
Đưa thừa số vào trong dấu căn
+) $A\sqrt B = \sqrt {{A^2}B} $ với $A \ge 0$ và $B \ge 0$
+) $A\sqrt B = - \sqrt {{A^2}B} $ với $A < 0$ và $B \ge 0$
Công thức khai phương một tích
$\sqrt {AB} = \sqrt A .\sqrt B \,\,\left( {A \ge 0;B \ge 0} \right)$
Ta có \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \)$ = 5\sqrt a - 4\sqrt {25{a^3}{b^2}} + 5\sqrt {16a{b^2}.{a^2}} - \sqrt 9 .\sqrt a $
$ = 5\sqrt a - 4\sqrt {25} .\sqrt {{a^3}{b^2}} + 5\sqrt {16} .\sqrt {{a^3}{b^2}} - 3\sqrt a $$ = \left( {5\sqrt a - 3\sqrt a } \right) - \left( {4.5\sqrt {{a^3}{b^2}} - 5.4\sqrt {{a^3}{b^2}} } \right)$$ = 2\sqrt a $
Rút gọn biểu thức \(2\sqrt a - \sqrt {9{a^3}} + {a^2}\sqrt {\dfrac{{16}}{a}} + \dfrac{2}{{{a^2}}}\sqrt {36{a^5}} \) với $a > 0$ ta được
-
A.
$14\sqrt a + a\sqrt a $
-
B.
$14\sqrt a - a\sqrt a $
-
C.
$14\sqrt a + 2a\sqrt a $
-
D.
$20\sqrt a - 2a\sqrt a $
Đáp án : A
-Sử dụng công thức khai phương một thương \(\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt A }}{{\sqrt B }}\) với \(A \ge 0,B > 0\) và công thức khai phương một tích \(\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)\)
-Khử mẫu biểu thức lấy căn theo công thức \(\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{B}\,\left( {A \ge 0,B > 0} \right)\)
-Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\)
-Cộng trừ các căn thức bậc hai.
Với $a>0$ ta có \(2\sqrt a - \sqrt {9{a^3}} + {a^2}\sqrt {\dfrac{{16}}{a}} + \dfrac{2}{{{a^2}}}\sqrt {36{a^5}} \)$ = 2\sqrt a - \sqrt {9{a^2}.a} + {a^2}\dfrac{{\sqrt {16a} }}{a} + \dfrac{2}{{{a^2}}}.\sqrt {36{a^4}.a} $
$ = 2\sqrt a - 3a\sqrt a + 4a\sqrt a + \dfrac{2}{{{a^2}}}.6{a^2}\sqrt a $$ = 2\sqrt a - 3a\sqrt a + 4a\sqrt a + 12\sqrt a = 14\sqrt a + a\sqrt a $
Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng $d:y = \left( {m + 2} \right)x - m$ và $d':y = - 2x - 2m + 1$. Với giá trị nào của $m$ thì $d$ cắt $d'$?
-
A.
$m \ne - 2$
-
B.
$m \ne - 4$
-
C.
$m \ne \left\{ { - 2; - 4} \right\}$
-
D.
$m \ne \left\{ {2; - 4} \right\}$
Đáp án : C
+) Tìm điều kiện để hàm số $y=ax+b$ là hàm số bậc nhất là $a\ne 0$
+) Sử dụng vị trí tương đối giữa hai đường thẳng:
Cho hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$.
+) $d{\rm{//}}d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$
+) \(d\) cắt $d'$\( \Leftrightarrow a \ne a'\).
+) \(d \equiv d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\).
+) \(d \bot d' \Leftrightarrow a.a' = - 1\).
+) Ta thấy $d:y = \left( {m + 2} \right)x - m$ có $a = m + 2$ và $d':y = - 2x - 2m + 1$ có $a' = - 2$ .
+) Để $y = \left( {m + 2} \right)x - m$ là hàm số bậc nhất thì $m + 2 \ne 0 \Leftrightarrow m \ne - 2$
+) Để \(d\) cắt $d'$\( \Leftrightarrow a \ne a'\)
$ \Leftrightarrow m + 2 \ne - 2 \Leftrightarrow m \ne - 4$
Vậy $m \ne \left\{ { - 2; - 4} \right\}$.
Cho hệ phương trình $\left\{ \begin{array}{l}2x + by = - 1\\bx - 2ay = 1\end{array} \right.$. Biết rằng hệ phương trình có nghiệm là $\left( {1; - 2} \right)$, tính $a - b$.
-
A.
$\dfrac{{13}}{8}$
-
B.
$ - \dfrac{{13}}{8}$
-
C.
$\dfrac{5}{8}$
-
D.
$ - \dfrac{5}{8}$
Đáp án : B
Hệ phương trình bậc nhất hai ẩn có nghiệm $\left( {{x_0};{y_0}} \right) \Leftrightarrow \left\{ \begin{array}{l}a{x_0} + b{y_0} = c\\a'{x_0} + b'{y_0} = c'\end{array} \right..$
Thay $x = 1;y = - 2$ vào hệ ta được
$\left\{ \begin{array}{l}2.1 + b.\left( { - 2} \right) = - 1\\b.1 - 2a.\left( { - 2} \right) = 1\end{array} \right.$
$\left\{ \begin{array}{l} - 2b = - 3\\b + 4a = 1\end{array} \right.$
$\left\{ \begin{array}{l}b = \dfrac{3}{2}\\\dfrac{3}{2} + 4a = 1\end{array} \right.$
$\left\{ \begin{array}{l}b = \dfrac{3}{2}\\a = - \dfrac{1}{8}\end{array} \right.$
$a - b = - \dfrac{{13}}{8}$
Vậy $a - b = - \dfrac{{13}}{8}$.
Cho hệ phương trình $\left\{ \begin{array}{l}(m - 1)x + y = 2\\mx + y = m + 1\end{array} \right.$ ( $m$ là tham số) . Kết luận nào sau đây là đúng khi nói về nghiệm $\left( {x;y} \right)$ của hệ phương trình
-
A.
Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y \le {\rm{3}}$
-
B.
Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y > {\rm{3}}$
-
C.
Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y \ge {\rm{3}}$
-
D.
Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y = {\rm{3}}$
Đáp án : A
Bước 1: Giải hệ phương trình tìm được nghiệm $\left( {x,y} \right)$ theo tham số $m$
Bước 2: Thay $x,y$ vừa tìm được vào hệ thức yêu cầu để tìm $m$
Từ $\left( {m - 1} \right)x + y = 2$ thế vào phương trình còn lại ta được phương trình:
$mx + 2-\left( {m - 1} \right)x = m + 1 \Leftrightarrow x = m-1$ suy ra $y = 2-{\left( {m - 1} \right)^2}$ với mọi $m$
Vậy hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right) = \left( {m - 1;2-{{\left( {m - 1} \right)}^2}} \right)$
$2x + {\rm{ }}y = 2\left( {m - 1} \right) + 2-{\left( {m - 1} \right)^2} = - {m^2} + 4m - 1$
$= 3-{\left( {m - 2} \right)^2} \le 3$ với mọi $m$.
Một mảnh đất hình chữ nhật có chu vi bằng $42$ m. Đường chéo hình chữ nhật dài $15$ m. Tính độ dài chiều rộng mảnh đất hình chữ nhật.
-
A.
$10\,\,m$
-
B.
$12\,\,m$
-
C.
$9\,\,m$
-
D.
$8\,\,m$
Đáp án : C
Giải bài toán có nội dung hình học bằng cách lập hệ phương trình.
Chú ý các công thức:
+ Chu vi hình chữ nhật $ = $ ( Chiều dài $ + $ chiều rộng)$.2$
+ Định lý Pitago: " Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông"
Gọi chiều dài và chiều rộng của mảnh đất hình chữ nhật lần lượt là $x,y\,\,\left( {21 > x > y > 0;\,m} \right)$
Vì khu vườn hình chữ nhật có chu vi bằng $42$ $m$ nên ta có $\left( {x + y} \right).2 = 42$
Đường chéo hình chữ nhật dài $15$$m$ nên ta có phương trình ${x^2} + {y^2} = {15^2}$
Suy ra hệ phương trình $\left\{ \begin{array}{l}\left( {x + y} \right).2 = 42\\{x^2} + {y^2} = 225\end{array} \right.$
$\left\{ \begin{array}{l}x + y = 21\\{x^2} + {y^2} = 225\end{array} \right.$
$ \left\{ \begin{array}{l}y = 21 - x\\{x^2} + {\left( {21 - x} \right)^2} = 225\,\,\left( 1 \right)\end{array} \right.$
Giải phương trình $\left( 1 \right)$ ta được
$2{x^2} - 42x + 216 = 0 \\ {x^2} - 21x + 108 = 0 \\ \left( {x - 12} \right)\left( {x - 9} \right) = 0 $
$x = 12, y = 9\,\left( N \right)$ hoặc $x = 9, y = 12\,\,\left( L \right)$
Vậy chiều rộng mảnh đất ban đầu là $9\,\,m$.
Một canô chạy trên sông trong $7$ giờ, xuôi dòng \(108\,km\) và ngược dòng \(63\,km\) . Một lần khác cũng trong 7 giờ canô xuôi dòng \(81\,km\) và ngược dòng \(84\,km\) . Tính vận tốc nước chảy.
-
A.
$4\,{\rm{km/h}}$
-
B.
$3\,{\rm{km/h}}$
-
C.
$2\,{\rm{km/h}}$
-
D.
$2,5\,{\rm{km/h}}$
Đáp án : B
Giải bài toán chuyển động bằng cách lập hệ phương trình.
Chú ý: Công thức liên quan đến chuyển động của tàu, cano.. trên dòng nước
Vận tốc xuôi dòng $ = $ vận tốc ca nô (tàu) $ + $ vận tốc dòng nước
Vận tốc ngược dòng $ = $ vận tốc ca nô (tàu) $ - $ vận tốc dòng nước
Gọi vận tốc thực của canô là $x\,\,\left( {{\rm{km/h}},x > 0} \right)$, vận tốc dòng nước là $y\,\,\left( {{\rm{km/h}},0 < y < x} \right)$
Vận tốc cano khi xuôi dòng là $x + y\,\,\left( {{\rm{km/h}}} \right)$, vận tốc cano khi ngược dòng là $x - y\,\,\left( {{\rm{km/h}}} \right)$
Canô chạy trên sông trong $7$ giờ, xuôi dòng \(108\,km\) và ngược dòng \(63\,km\) nên ta có phương trình
$\dfrac{{108}}{{x + y}} + \dfrac{{63}}{{x - y}} = 7$
Canô chạy trên sông trong $7$ giờ canô xuôi dòng \(81\,km\) và ngược dòng \(84\,km\) nên ta có phương trình
$\dfrac{{81}}{{x + y}} + \dfrac{{84}}{{x - y}} = 7$
Ta có hệ phương trình
$\left\{ \begin{array}{l}\dfrac{{108}}{{x + y}} + \dfrac{{63}}{{x - y}} = 7\\\dfrac{{81}}{{x + y}} + \dfrac{{84}}{{x - y}} = 7\end{array} \right.$
Đặt \(a = \frac{1}{x+y}, b = \frac{1}{x-y}\), hệ phương trình trở thành:
$\left\{ \begin{array}{l}108a + 63b = 7\\81a + 84b = 7\end{array} \right.$
Nhân phương trình thứ nhất với 4, nhân phương trình thứ hai với 3, ta được:
$\left\{ \begin{array}{l}432a + 252b = 28\\243a + 252b = 21\end{array} \right.$
Trừ hai vế của phương trình thứ nhất cho phương trình thứ hai, ta được:
$432a + 252b - \left(243a + 252b \right) = 28 - 21$ $189a = 7$
$a = \frac{1}{27}$, thay vào $81a + 84b = 7$ ta được $b = \frac{1}{21}$
Suy ra $x + y = 27;x - y = 21$
Ta tính được \(x = \frac{27 + 21}{2} = 24; y = \frac{27 - 21}{2} = 3\) (TM)
Vậy vận tốc dòng nước là $3\,\,{\rm{km/h}}.$
Cho phương trình \(\left( {m - 3} \right){x^2} - 2mx + m - 6 = 0\). Tìm các giá trị của $m$ để phương trình vô nghiệm
-
A.
$m < - 2$
-
B.
$m < 2$
-
C.
$m < 3$
-
D.
$m < - 3$
Đáp án : B
Xét phương trình bậc hai dạng $a{x^2} + bx + c = 0$ với $b = 2b'$
TH1: $a = 0$
TH2: $a \ne 0$. Khi đó, p hương trình vô nghiệm\( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' < 0\end{array} \right.\)
Phương trình \(\left( {m - 3} \right){x^2} - 2mx + m - 6 = 0\) có $a = m - 3;b' = - m;c = m - 6$
Suy ra $\Delta ' = {m^2} - \left( {m - 3} \right)\left( {m - 6} \right) = 9m - 18$
TH1: $m - 3 = 0 \Leftrightarrow m = 3 \Rightarrow - 6x - 3 = 0 \Leftrightarrow x = - \dfrac{1}{2}$
TH2: $m - 3 \ne 0 \Leftrightarrow m \ne 3$
Để phương trình có vô nghiệm phân biệt thì $\left\{ \begin{array}{l}a \ne 0\\\Delta ' < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 3\\9m - 18 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 3\\m < 2\end{array} \right. \Rightarrow m < 2$
Vậy $m < 2$ là giá trị cần tìm.
Tìm các giá trị của \(m\) để phương trình \({x^2} - 2\left( {m - 3} \right)x + 8 - 4m = 0\) có hai nghiệm âm phân biệt.
-
A.
$m < 2$ và $m \ne 1$
-
B.
$m < 3$
-
C.
$m <2$
-
D.
$m > 0$
Đáp án : A
Xét phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm âm phân biệt khi \(\Delta > 0\) (\(\Delta ' > 0\)), \(P > 0\) và \(S < 0\).
Phương trình \({x^2} - 2\left( {m - 3} \right)x + 8 - 4m = 0\) có $ {a = 1;b' = - \left( {m - 3} \right);c = 8 - 4m} $
Ta có $\Delta ' = {\left( {m - 3} \right)^2} - \left( {8 - 4m} \right) $$= {m^2} - 2m + 1 = {\left( {m - 1} \right)^2}$;
Áp dụng định lí Viète, ta có: $S = {x_1} + {x_2} = 2\left( {m - 3} \right);$$P = {x_1}.{x_2} = 8 - 4m$
Phương trình có hai nghiệm âm phân biệt khi:
+) \(\Delta ' > 0\) hay \({\left( {m - 1} \right)^2} > 0\) suy ra \(m \ne 1\)
+) $S = {x_1} + {x_2} < 0$ hay $2\left( {m - 3} \right) < 0$ suy ra $m < 3$
+) $P = {x_1}.{x_2} > 0$ hay $8 - 4m > 0$ suy ra \(m < 2\)
Kết hợp 3 điều kiện trên, ta được \(m \ne 1\) và \(m < 2\)
Vậy $m < 2$ và $m \ne 1$ là giá trị cần tìm.
Biết rằng phương trình $\left( {m - 2} \right){x^2} - \left( {2m + 5} \right)x + m + 7 = 0\,\left( {m \ne 2} \right)$ luôn có nghiệm ${x_1};{x_2}$ với mọi $m$. Tìm ${x_1};{x_2}$ theo $m$.
-
A.
${x_1} = - 1;{x_2} = - \dfrac{{m + 7}}{{m - 2}}$
-
B.
${x_1} = 1;{x_2} = - \dfrac{{m + 7}}{{m - 2}}$
-
C.
${x_1} = 1;{x_2} = \dfrac{{m + 7}}{{m - 2}}$
-
D.
${x_1} = - 1;{x_2} = \dfrac{{m + 7}}{{m - 2}}$
Đáp án : C
Sử dụng cách nhẩm nghiệm:
Xét phương trình bậc hai $a{x^2} + bx + c = 0{\rm{ }}\left( {a \ne 0} \right)$.
+) Nếu phương trình có $a + b + c = 0$ thì phương trình có một nghiệm ${x_1} = 1$, nghiệm kia là ${x_2} = \dfrac{c}{a}.$
+ ) Nếu phương trình có $a - b + c = 0$ thì phương trình có một nghiệm ${x_1} = - 1$, nghiệm kia là ${x_2} = - \dfrac{c}{a}.$
Phương trình $\left( {m - 2} \right){x^2} - \left( {2m + 5} \right)x + m + 7 = 0$ có $a = m - 2;b = - 2m - 5;c = m + 7$
Vì $a + b + c = m - 2 - 2m - 5 + m + 7 = 0$ nên phương trình có hai nghiệm ${x_1} = 1;{x_2} = \dfrac{{m + 7}}{{m - 2}}$.
Số nghiệm của phương trình \(3{x^3} + 3{x^2} + 5x + 5 = 0\) là:
-
A.
$2$
-
B.
$0$
-
C.
$1$
-
D.
$3$
Đáp án : C
Ta có \(3{x^3} + 3{x^2} + 5x + 5 = 0\)$ \Leftrightarrow 3{x^2}\left( {x + 1} \right) + 5\left( {x + 1} \right) = 0 \Leftrightarrow \left( {3{x^2} + 5} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 5 = 0\\x + 1 = 0\end{array} \right.$
$ \Leftrightarrow \left[ \begin{array}{l}3{x^2} = - 5\left( L \right)\\x = - 1\end{array} \right. \Rightarrow x = - 1$
Vậy phương trình có nghiệm duy nhất $x = - 1$.
Một ca nô chạy xuôi dòng với quãng đường $42{\rm{km}}$, rồi sau đó ngược dòng trở lại $20{\rm{ km}}$ hết tổng cộng $5{\rm{h}}$. Biến vận tốc của dòng nước chảy là $2{\rm{ km/h}}$. Tính vận tốc của ca nô lúc dòng nước yên lặng.
-
A.
$11{\rm{ }}\left( {{\rm{km/h}}} \right)$
-
B.
$12{\rm{ }}\left( {{\rm{km/h}}} \right)$
-
C.
$14{\rm{ }}\left( {{\rm{km/h}}} \right)$
-
D.
$15{\rm{ }}\left( {{\rm{km/h}}} \right)$
Đáp án : B
Gọi vận tốc của ca nô lúc dòng nước yên lặng là $x{\rm{ }}\left( {{\rm{km/h}}} \right);\left( {x > {\rm{2}}} \right)$
Vì vận tốc nước là $2{\rm{ km/h}}$ nên vận tốc xuôi dòng và ngược dòng lần lượt là $x{\rm{ }} + {\rm{ }}2$ và $x{\rm{ - }}2{\rm{ }}\left( {{\rm{km/h}}} \right)$
Thời gian để ca nô đi hết $42{\rm{ km}}$ xuôi dòng là $\dfrac{{42}}{{x + 2}}{\rm{(h)}}$
Thời gian để ca nô đi hết $20{\rm{ km}}$ ngược dòng là $\dfrac{{20}}{{x - 2}}{\rm{(h)}}$
Tổng thời gian là $5{\rm{h}}$ do đó
$\dfrac{{42}}{{x + 2}} + \dfrac{{20}}{{x - 2}} = 5 \Leftrightarrow \dfrac{{42(x - 2) + 20(x + 2)}}{{(x - 2)(x + 2)}} = 5 \Leftrightarrow \dfrac{{62x - 44}}{{{x^2} - 4}} = 5$
$ \Rightarrow 5{x^2} - 62x + 24 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 12{\rm{(TM)}}\\x = 0,4{\rm{(L)}}\end{array} \right.$
Vậy vận tốc của ca nô khi nước yên lặng là $12{\rm{ km/h}}$ .
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
-
A.
$DE$ là cát tuyến của đường tròn đường kính $BH$
-
B.
$DE$ là tiếp tuyến của đường tròn đường kính $BH$
-
C.
Tứ giác$AEHD$ là hình chữ nhật
-
D.
$DE \bot DI$ (với $I$ là trung điểm $BH$)
Đáp án : A
Sử dụng dấu hiệu nhận biết các hình đặc biệt và cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.
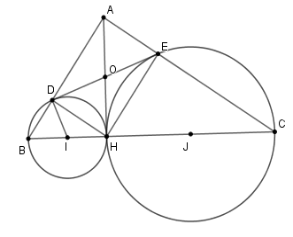
Gọi $I$, $J$ lần lượt là trung điểm của $BH$ và $CH.$
Để chứng minh $DE$ là tiếp tuyến của đường tròn tâm $I$ đường kính $BH$ ta chứng minh
\(ID \bot DE\) hay $\widehat {ODI} = {90^o}$
Vì $D,E$ lần lượt thuộc đường tròn đường kính $BH$ và $HC$ nên ta có: $\widehat {BDH} = \widehat {CEH} = {90^0}$
Suy ra tứ giác $ADHE$ là hình chữ nhật.
Gọi $O$ là giao điểm của $AH$ và$DE$, khi đó ta có $OD = OH = OE = OA$ .
Suy ra $\Delta ODH$ cân tại $O \Rightarrow \widehat {ODH} = \widehat {OHD}$
Ta cũng có $\Delta IDH$ cân tại $I$$ \Rightarrow \widehat {IDH} = \widehat {IHD}$
Từ đó $ \Rightarrow \widehat {IDH} + \widehat {HDO} = \widehat {IHD} + \widehat {DHO} \Rightarrow \widehat {IDO} = 90^\circ $$ \Rightarrow ID \bot DE$
Ta có \(ID \bot DE,D \in \left( I \right)\) nên $DE$ là tiếp tuyến của đường tròn đường kính $BH$.
Từ chứng minh trên suy ra các phương án B,C,D đúng.
Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
-
A.
$18\,cm$
-
B.
$6\sqrt 3 cm$
-
C.
$12\sqrt 3 \,cm$
-
D.
$15\,cm$
Đáp án : A
Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác
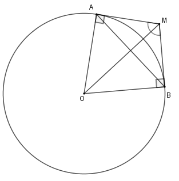
Xét $\left( O \right)$ có $MA = MB$; $\widehat {AMO} = \widehat {BMO}$ (tính chất hai tiếp tuyến cắt nhau)
Nên $\widehat {AMO} = 60^\circ $. Xét tam giác vuông $AOM$ có $AM = AO.cot\widehat {AMO} = \dfrac{{R\sqrt 3 }}{3}$ nên $MA = MB = \dfrac{{R\sqrt 3 }}{3}$
Lại có $\widehat {AOB} + \widehat {AMB} = 180^\circ \Rightarrow \widehat {AOB} = 60^\circ $ suy ra $\Delta AOB$ là tam giác đều $ \Rightarrow AB = OB = OA = R$
Chu vi tam giác $MAB$ là $MA + MB + AB = \dfrac{{R\sqrt 3 }}{3} + \dfrac{{R\sqrt 3 }}{3} + R = 6\left( {3 + 2\sqrt 3 } \right)$
hay $ R\left( {\dfrac{{3 + 2\sqrt 3 }}{3}} \right) = 6\left( {3 + 2\sqrt 3 } \right) \Rightarrow R = 18\,cm$ nên $AB = 18\,cm$.
Cho hai đường tròn $\left( {O;20cm} \right)$ và $\left( {O';15cm} \right)$ cắt nhau tại $A$ và$B$. Tính đoạn nối tâm $OO'$, biết rằng$AB = 24cm$ và $O$ và $O'$ nằm cùng phía đối với $AB$ .
-
A.
$OO' = 7cm$
-
B.
$OO' = 8cm$
-
C.
$OO' = 9cm$
-
D.
$OO' = 25cm$
Đáp án : A
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và định lý Pytago
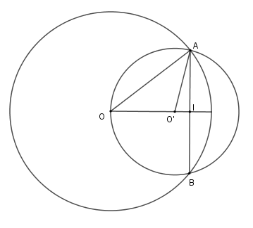
Ta có: $AI = \dfrac{1}{2}AB = 12\,\ cm$
Theo định lý Pytago ta có
$O{I^2} = O{A^2}-A{I^2} = 256$ $ \Rightarrow $ $OI = 16 \,\ cm$ và $O'I = \sqrt {O'{A^2} - I{A^2}} = 9 \,\ cm$
Do đó: $OO' = OI-O'I = 16-9 = 7\left( {cm} \right)$ .
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
-
A.
\(AD.AE\)
-
B.
\(AD.AC\)
-
C.
\(AE.BE\)
-
D.
\(AD.BD\)
Đáp án : A
Sử dụng hệ quả của góc nội tiếp để chứng minh các góc bằng nhau và suy ra tam giác đồng dạng
Từ đó có hệ thức cần chứng minh.
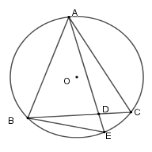
Xét \(\left( O \right)\) có \(\widehat {AEB} = \widehat {ABC}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AB = AC\) )
Xét \(\Delta ABD\) và \(\Delta AEB\) có \(\widehat A\) chung và \(\widehat {AEB} = \widehat {ABC}\) (cmt) nên \(\Delta ABD\backsim\Delta AEB\left( {g - g} \right) \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AE.AD\)
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
-
A.
\(A{B^2}\)
-
B.
\(B{C^2}\)
-
C.
\(A{C^2}\)
-
D.
\(A{M^2}\)
Đáp án : A
Sử dụng hệ quả về góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
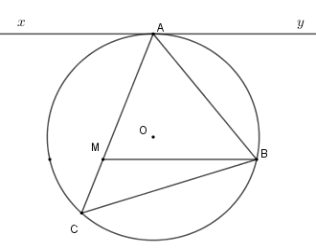
Ta có \(\widehat {yAB} = \widehat {ACB}\) (hệ quả) mà \(\widehat {yAB} = \widehat {ABM}\) (so le trong) nên \(\widehat {ACB} = \widehat {ABM} \Rightarrow \Delta AMB\backsim\Delta ABC\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow AM.AC = A{B^2}\) .
Cho đường tròn $\left( O \right)$ đường kính $AB$. Gọi $I$ là trung điểm của $OA$ . Dây $CD$ vuông góc với $AB$ tại $I$. Lấy $K$ tùy ý trên cung $BC$ nhỏ, $AK$ cắt $CD$ tại $H$. Khẳng định nào đúng ?
-
A.
Tứ giác $BIHK$ nội tiếp.
-
B.
Tứ giác $BIHK$ không nội tiếp.
-
C.
Tứ giác $BIHK$ là hình chữ nhật.
-
D.
Các đáp án trên đều sai.
Đáp án : A
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.
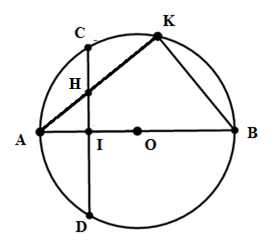
Ta có: \(\widehat {AKB}\) là góc nội tiếp chắn nửa đường tròn (O) suy ra \( \widehat {AKB} = {90^0}.\)
Tam giác HKB có \(\widehat {HKB} = {90^0}\) và tam giác HIB có \(\widehat {HIB} = {90^0}\left( {do\;\;CD \bot AB } \right)\) nên tam giác HKB và tam giác HIB vuông và nội tiếp đường tròn đường kính HB.
Do đó tứ giác HKBI là tứ giác nội tiếp (bốn đỉnh H, K, B, I cùng thuộc đường tròn đường kính HB).
Vậy A đúng, B sai.
Lại có \(\widehat {KBA} < {90^0}\) do \(\Delta AKB\) vuông tại \(K\) nên \(KBIH\) không là hình chữ nhật. Do đó C sai.
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Đáp án : D
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
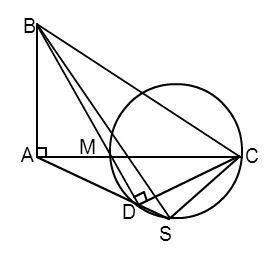
+) Ta có: \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn đường kính $MC$ \( \Rightarrow \widehat {MDC} = {90^0}\) (tính chất góc nội tiếp).
Xét tứ giác $ABCD$ ta có:
Góc $BAC$ và góc $BDC$ cùng nhìn đoạn $BC$ dưới góc \({90^0}.\)
\( \Rightarrow \) $ABCD$ là tứ giác nội tiếp (dhnb) \( \Rightarrow \) phương án A đúng.
+) Xét tứ giác $ABCD$ nội tiếp ta có\(\widehat {ABD} = \widehat {ACD}\) (cùng nhìn đoạn $AD$ )\( \Rightarrow \) phương án B đúng.
+) Xét đường tròn đường kính $MC$ ta có $4$ điểm $M,C,D,S$ cùng thuộc đường tròn.
\( \Rightarrow \) Tứ giác $MCSD$ là tứ giác nội tiếp.
\( \Rightarrow \widehat {ADM} = \widehat {SCM}\) (góc ngoài tại $1$ đỉnh bằng góc trong tại đỉnh đối diện). $\left( 1 \right)$
Vì tứ giác $ABCD$ nội tiếp (cmt) \( \Rightarrow \widehat {ACB} = \widehat {ADB}\) (cùng nhìn đoạn$AB$ ) $\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ \( \Rightarrow \widehat {BCA} = \widehat {ACS}\;\;\;\left( { = \widehat {ADB}} \right).\)
Hay $CA$ là phân giác của \(\widehat {SCB} \Rightarrow \) phương án C đúng.
+) Giả sử tứ giác $ABCS$ là tứ giác nội tiếp \( \Rightarrow \widehat {ASB} = \widehat {BCA}\) (hai góc cùng nhìn đoạn $AB$ ).
Mà \(\widehat {ACB} = \widehat {BDA};\;\;\;\widehat {BAD} \ne \widehat {BSA}\) (xét trong đường tròn đường kính $CM$ )
\( \Rightarrow \widehat {ASB} \ne \widehat {BCA} \Rightarrow \) tứ giác $ABCS$ không là tứ giác nội tiếp \( \Rightarrow \)phương án D sai.
Cho tam giác đều \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \). Diện tích của tam giác đều \(ABC\) là:
-
A.
\(27\sqrt 3 \) $cm^2$
-
B.
\(7\sqrt 3 \) $cm^2$
-
C.
\(29\sqrt 3 \) $cm^2$
-
D.
\(9\sqrt 3 \) $cm^2$
Đáp án : A
+ Áp dụng công thức tính chu vi hình tròn
+ Tính chất của tam giác cân
+ Sử dụng định lý Pitago
+ Sử dụng công thức tính diện tích tam giác
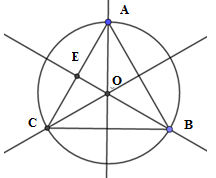
Gọi \(R\) là bán kính của đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \) nên ta có \(C = 2\pi R = 4\pi + 4\pi + 4\pi = 12\pi \), suy ra \(R = 6\) hay \(OA = OB = OC = 6\)
Ta cũng có \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\) suy ra \(\Delta AOB = \Delta AOC = \Delta BOC = \dfrac{1}{3}\Delta ABC\)
Xét tam giác \(AOC\) có: \(\left\{ \begin{array}{l}\widehat {OAC} = \widehat {OCA} = {30^0}\\\widehat {COA} = {120^0}\end{array} \right.\)
Kẻ đường cao$OE$ , ta có đồng thời là đường trung tuyến, phân giác của góc \(\widehat {COA}\) . Ta có \(\widehat {AOE} = \widehat {COE} = \dfrac{1}{2}\widehat {AOC}\)
Xét tam giác $COE$ có: \(\left\{ \begin{array}{l}\widehat {ECO} = {30^0}\\\widehat {CEO} = {90^0}\end{array} \right. \Rightarrow OE = \dfrac{1}{2}CO = \dfrac{R}{2}\)
Áp dụng định lý Pytago ta có: \(CE = \sqrt {O{C^2} - O{E^2}} = \sqrt {{R^2} - {{\left( {\dfrac{R}{2}} \right)}^2}} = \dfrac{{\sqrt 3 }}{2}R\)
Vậy \({S_{COE}} = \dfrac{1}{2}OE.CE = \dfrac{1}{2}.\dfrac{R}{2}.\dfrac{{\sqrt 3 R}}{2} = \dfrac{{\sqrt 3 {R^2}}}{8}\)
Suy ra \({S_{COA}} = 2{S_{COE}} = \dfrac{{\sqrt 3 {R^2}}}{4}\) và \({S_{ABC}} = 3{S_{COA}} = \dfrac{{3\sqrt 3 {R^2}}}{4} = \dfrac{{3\sqrt 3 {R^2}}}{4} = 27\sqrt 3 \,\ cm^2 .\)