Đề kiểm tra học kì 1 Toán 9 - Đề số 27 — Không quảng cáo

Đề bài

Câu 1: (2,0 điểm)

1) Thực hiện phép tính :

a) $\sqrt {20}  - 3\sqrt {125}  + 5\sqrt {45}$

b) $\frac{3}{{\sqrt 3  - \sqrt 2 }} - 2\sqrt {{{\left( {\sqrt 2  - \sqrt 3 } \right)}^2}}  - 5\sqrt 2$

2) Một cột cờ vuông góc với mặt đất có bóng dài $12m$, tia nắng của mặt trời tạo với mặt đất một góc là ${35^0}$ (hình vẽ bên). Tính chiều cao của cột cờ.

Câu 2: (2,0 điểm)

Cho các biểu thức: $A = \frac{{\sqrt x }}{{\sqrt x  + 2}};\,\,\,\,\,\,\,\,B = \frac{x}{{x - 4}} - \frac{1}{{2 - \sqrt x }} + \frac{1}{{\sqrt x  + 2}}$ (với $x \ge 0;\,\,x \ne 4$)

a) Tính giá trị của biểu thức $A$ khi $x = 36$.

b) Rút gọn $B$.

c) Tìm các giá trị nguyên của $x$ để biểu thức $P = A.B$ có giá trị là số nguyên

Câu 3: Cho hàm số bậc nhất $y = \left( {m + 1} \right)x + 2$ có đồ thị $\left( d \right)$ ($m$ là tham số và $m \ne  - 1$)

a) Vẽ $\left( d \right)$ khi $m = 0$.

b) Xác định $m$ để đường thẳng $\left( d \right)$ song song với đường thẳng $y = 2x + 1$.

c) Xác định $m$ để $\left( d \right)$ cắt hai trục $Ox,Oy$ tại $A$ và $B$ sao cho tam giác $AOB$ có diện tích bằng $2$ ( đơn vị diện tích ).

Câu 4: (3,5 điểm)

Cho nửa đường tròn tâm $O$, đường kính $AB = 2R$. Trên nửa mặt phẳng có bờ là $AB$ chứa nửa đường tròn, vẽ tiếp tuyến $Ax,\,\,By$. Từ điểm $M$ tùy ý thuộc nửa đường tròn ($M$khác $A,B$) vẽ tiếp tuyến tại $M$ cắt $Ax,\,\,By$ lần lượt tại $C,\,\,D$. Gọi $E$ là giao điểm của $CO$ và $AM$, $F$là giao điểm của $DO$ và $BM$.

a) Chứng minh $4$điểm $A,C,M,O$ cùng thuộc một đường tròn.

b) Chứng minh $AC + BD = CD$ và tứ giác $MEOF$ là hình chữ nhật.

c) Chứng minh tích $AC.BD$ không đổi khi $M$ di động trên nửa đường tròn.

d) Tìm vị trí của $M$ trên nửa đường tròn sao cho diện tích tứ giác $ABDC$ nhỏ nhất.

Câu 5: (0,5 điểm)

Tìm giá trị lớn nhất của biểu thức: $A = \sqrt {x - 2}  + 2\sqrt {x + 1}  + 2019 - x$.

-------- Hết --------

Lời giải

Câu 1: (2,0 điểm)

1) Thực hiện phép tính :

a) $\sqrt {20}  - 3\sqrt {125}  + 5\sqrt {45}$

b) $\frac{3}{{\sqrt 3  - \sqrt 2 }} - 2\sqrt {{{\left( {\sqrt 2  - \sqrt 3 } \right)}^2}}  - 5\sqrt 2$

2) Một cột cờ vuông góc với mặt đất có bóng dài $12m$, tia nắng của mặt trời tạo với mặt đất một góc là ${35^0}$ (hình vẽ bên). Tính chiều cao của cột cờ.

Phương pháp

1) a) Sử dụng công thức đưa thừa số ra ngoài dấu căn : Với $B \ge 0$ ta có : $\sqrt {{A^2}B}  = \left| A \right|B = \left\{ \begin{array}{l}AB\,\,\,\,khi\,\,\,\,A \ge 0\\ - AB\,\,\,khi\,\,\,\,A < 0\end{array} \right..$

b) Sử dụng hằng đẳng thức $\sqrt {{A^2}}  = \left| A \right|$  và trục căn thức ở mẫu : $\frac{m}{{\sqrt A  - \sqrt B }} = \frac{{m\left( {\sqrt A  + \sqrt B } \right)}}{{A - B}}\,\,\,\left( {A,B \ge 0;A \ne B} \right)$

2) Sử dụng quan hệ giữa cạnh và góc trong tam giác.

Trong tam giác vuông, cạnh góc vuông này bằng cạnh góc vuông còn lại nhân tan góc đối.

Lời giải

1)

$\begin{array}{l}a)\,\,\sqrt {20}  - 3\sqrt {125}  + 5\sqrt {45} \\ = 2\sqrt 5  - 15\sqrt 5  + 15\sqrt 5 \\ = 2\sqrt 5 \end{array}$

$\begin{array}{l}b)\,\,\frac{3}{{\sqrt 3  - \sqrt 2 }} - 2\sqrt {{{\left( {\sqrt 2  - \sqrt 3 } \right)}^2}}  - 5\sqrt 2 \\ = \frac{{3\left( {\sqrt 3  + \sqrt 2 } \right)}}{{3 - 2}} - 2\left| {\sqrt 2  - \sqrt 3 } \right| - 5\sqrt 2 \\ = 3\sqrt 3  + 3\sqrt 2  - 2\left( {\sqrt 3  - \sqrt 2 } \right) - 5\sqrt 2 \\ = 3\sqrt 3  + 3\sqrt 2  - 2\sqrt 3  + 2\sqrt 2  - 5\sqrt 2 \\ = \sqrt 3 \end{array}$

2)

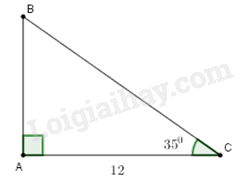Ta đưa về bài toán: Cho tam giác $ABC$ vuông tại $A$ có $AC = 12m,\,\,\,\angle BCA = {35^0}.$  Tính $AB.$

Chiều cao cột là $AB$.

Do $\Delta ABC$ vuông tại $A$ nên ta có :

$\begin{array}{l}AB = AC.\tan C\\\,\,\,\,\,\,\,\,\, = 12.\tan 35^\circ \\\,\,\,\,\,\,\,\,\, = 8,402\,\,\left( m \right)\end{array}$

Câu 2: Cho các biểu thức: $A = \frac{{\sqrt x }}{{\sqrt x  + 2}};\,\,\,\,\,\,\,\,B = \frac{x}{{x - 4}} - \frac{1}{{2 - \sqrt x }} + \frac{1}{{\sqrt x  + 2}}$ (với $x \ge 0;\,\,x \ne 4$)

a) Tính giá trị của biểu thức $A$ khi $x = 36$.

b) Rút gọn $B$.

c) Tìm các giá trị nguyên của $x$ để biểu thức $P = A.B$ có giá trị là số nguyên

Phương pháp

a) Thay $x = 36\left( {tmdk} \right)$ vào rồi tính toán.

b) Quy đồng mẫu các phân thức sau đó cộng các phân thức để rút gọn.

c) Đưa $P$ về dạng $P = a + \frac{b}{{f\left( x \right)}}\,\,\,\left( {a,b \in \mathbb{Z}} \right).$

Khi đó để $P \in \mathbb{Z} \Rightarrow f\left( x \right) \in U\left( b \right)$ từ đó tìm ra $x.$

Lời giải

a) Tính giá trị của biểu thức $A$ khi $x = 36$.

Điều kiện: $x \ge 0,\,\,\,x \ne 4.$

Thay $x = 36$ (Thỏa mãn đkxđ) vào biểu thức $A$ ta được:

$A = \frac{{\sqrt {36} }}{{\sqrt {36}  + 2}} = \frac{6}{{6 + 2}} = \frac{6}{8} = \frac{3}{4}$.

Vậy với $x = 36$ thì $A = \frac{3}{4}$.

b) Rút gọn $B$.

Điều kiện: $x \ge 0,\,\,\,x \ne 4.$

$\begin{array}{l}B = \frac{x}{{x - 4}} - \frac{1}{{2 - \sqrt x }} + \frac{1}{{\sqrt x  + 2}}\\\,\,\,\, = \frac{x}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 1} \right)}} + \frac{1}{{\sqrt x  - 2}} + \frac{1}{{\sqrt x  + 2}}\\\,\,\,\, = \frac{{x + \sqrt x  + 2 + \sqrt x  - 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 1} \right)}}\\\,\,\, = \frac{{x + 2\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 1} \right)}}\\\,\,\, = \frac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 1} \right)}} = \frac{{\sqrt x }}{{\sqrt x  - 2}}.\end{array}$

Vậy $B = \frac{{\sqrt x }}{{\sqrt x  - 2}}$ (với $x \ge 0;\,\,x \ne 4$).

c) Tìm các giá trị nguyên của $x$ để biểu thức $P = A.B$ có giá trị là số nguyên.

Với ĐKXĐ : $x \ge 0$ và $x \ne 4$ ta có:

$P = A.B = \frac{{\sqrt x }}{{\sqrt x  + 2}}.\frac{{\sqrt x }}{{\sqrt x  - 2}} = \frac{x}{{x - 4}}$ $= \frac{{x - 4 + 4}}{{x - 4}} = 1 + \frac{4}{{x - 4}}$

Do $x$ là số nguyên nên $x - 4$ là số nguyên.

Do đó: $P \in \mathbb{Z} \Leftrightarrow \frac{4}{{x - 4}} \in \mathbb{Z}$ $\Leftrightarrow x - 4 \in U\left( 4 \right) = \left\{ { - 4; - 2; - 1;\,\,1;\,\,2;\,\,4} \right\}$

Suy ra $x \in \left\{ {0;\,\,2;\,\,3;\,\,5;\,\,6;\,\,8} \right\}$.

Kết hợp với ĐKXĐ và $x$ là số nguyên ta được $x \in \left\{ {0;\,\,2;\,\,3;\,\,5;\,\,6;\,\,8} \right\}$.

Câu 3: (2,0 điểm)

Cho hàm số bậc nhất $y = \left( {m + 1} \right)x + 2$ có đồ thị $\left( d \right)$ ($m$ là tham số và $m \ne  - 1$)

a) Vẽ $\left( d \right)$ khi $m = 0$.

b) Xác định $m$ để đường thẳng $\left( d \right)$ song song với đường thẳng $y = 2x + 1$.

c) Xác định $m$ để $\left( d \right)$ cắt hai trục $Ox,Oy$ tại $A$ và $B$ sao cho tam giác $AOB$ có diện tích bằng $2$ ( đơn vị diện tích ).

Phương pháp

a)  Đường thẳng $\left( d \right):y = ax + b\,\left( {a \ne 0} \right)$ đi qua hai điểm có tọa độ $\left( {0;b} \right),\left( { - \frac{b}{a};0} \right).$

b) Hai đường thẳng $\left( d \right):y = ax + b,\,\left( {d'} \right):y = a'x + b'$ song song với nhau khi $\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right..$

c) Tính $OA,OB \Rightarrow {S_{OAB}} = \frac{1}{2}OA.OB.$

Lời giải

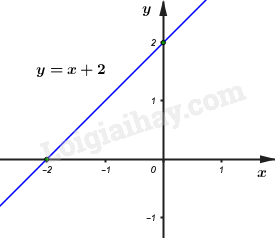
a) Khi $m = 0$ ta có $\left( d \right):\,y = x + 2$

Với $x = 0 \Rightarrow y = 2$

$x =  - 2 \Rightarrow y = 0$

Đồ thị hàm số $y = x + 2$ là đường thẳng $\left( d \right)$ đi qua hai điểm có tọa độ $\left( {0;2} \right),\left( { - 2;0} \right)$.

Hình vẽ:

b) Xác định $m$ để đường thẳng $\left( d \right)$ song song với đường thẳng $y = 2x + 1$.

Đường thẳng $\left( d \right)$ song song với đường thẳng $y = 2x + 1$

$\Leftrightarrow \left\{ \begin{array}{l}m + 1 = 2\\2 \ne 1\end{array} \right. \Leftrightarrow m = 1$

Kết hợp điều kiện $m \ne  - 1$ ta có $m = 1\,\,\left( {tm} \right).$

Vậy $m = 1$.

c) Xác định $m$ để $\left( d \right)$ cắt hai trục $Ox,Oy$ tại $A$ và $B$ sao cho tam giác $AOB$ có diện tích bằng $2$ (đơn vị diện tích)

Do $m \ne  - 1$ nên không mất tính tổng quát ta giả sử $\left( d \right)$ cắt $Ox$ và $Oy$ như hình vẽ

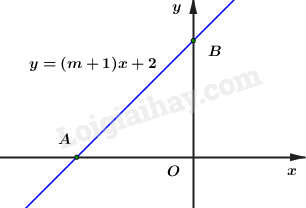
Vì $A$ là giao điểm của $\left( d \right)$ với $Ox$ nên $A\left( {x;0} \right) \Rightarrow \left( {m + 1} \right)x + 2 = 0 \Rightarrow x =  - \frac{2}{{m + 1}}$

Suy ra $A\left( { - \frac{2}{{m + 1}};0} \right) \Rightarrow OA = \frac{2}{{\left| {m + 1} \right|}}$

Vì $B$ là giao điểm của $\left( d \right)$ với $Oy$ nên $B\left( {0;y} \right) \Rightarrow \left( {m + 1} \right).0 + 2 = y \Rightarrow y = 2$

Suy ra $B\left( {0;2} \right) \Rightarrow OB = 2$

Vì $\Delta OAB$ vuông tại $O$.

Khi đó: ${S_{\Delta OAB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.\frac{2}{{\left| {m + 1} \right|}}.2 = \frac{2}{{\left| {m + 1} \right|}}$

Mà ${S_{\Delta OAB}} = 2 \Leftrightarrow \left| {m + 1} \right| = 1$ $\Leftrightarrow \left[ \begin{array}{l}m + 1 = 1\\m + 1 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m =  - 2\end{array} \right.$ (thỏa mãn $m \ne  - 1$)

Vạy $m = 0$ hoặc $m =  - 2$ thỏa mãn yêu cầu bài toán.

Câu 4: (3,5 điểm)

Cho nửa đường tròn tâm $O$, đường kính $AB = 2R$. Trên nửa mặt phẳng có bờ là $AB$ chứa nửa đường tròn, vẽ tiếp tuyến $Ax,\,\,By$. Từ điểm $M$ tùy ý thuộc nửa đường tròn ($M$khác $A,B$) vẽ tiếp tuyến tại $M$ cắt $Ax,\,\,By$ lần lượt tại $C,\,\,D$. Gọi $E$ là giao điểm của $CO$ và $AM$, $F$là giao điểm của $DO$ và $BM$.

a) Chứng minh $4$điểm $A,C,M,O$ cùng thuộc một đường tròn.

b) Chứng minh $AC + BD = CD$ và tứ giác $MEOF$ là hình chữ nhật.

c) Chứng minh tích $AC.BD$ không đổi khi $M$ di động trên nửa đường tròn.

d) Tìm vị trí của $M$ trên nửa đường tròn sao cho diện tích tứ giác $ABDC$ nhỏ nhất.

Phương pháp

a) Tam giác vuông nội tiếp đường tròn có đường kính là cạnh huyền của nó

b) Sử dụng tính chất hai tiếp tuyến cắt nhau và dấu hiệu : Tứ giác có ba góc vuông là hình chữ nhật

Chú ý : Tam giác nội tiếp đường tròn mà có 1 cạnh là đường kính của đường tròn thì tam giác đó là tam giác vuông.

c) Sử dụng hệ thức lượng trong tam giác vuông

d) Sử dụng kết quả câu b) câu c) và bất đẳng thức Cô-si cho hai số $a,b$ không âm : $a + b \ge 2\sqrt {ab}$

Dấu = xảy ra $\Leftrightarrow a = b.$

Lời giải

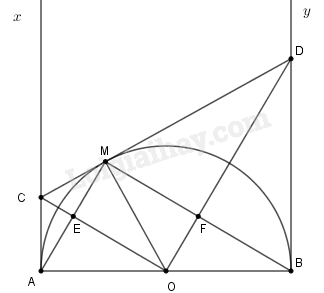
a) Chứng minh $4$điểm $A,C,M,O$ cùng thuộc một đường tròn.

Vì tam giá $\Delta OAC$ vuông tại $A$ nên nó nội tiếp đường tròn đường kính $CO$ (1)

Lại có $\Delta OMC$ vuông tại $M$ (do $MC$ là tiếp tuyến tại $M$) nên nó nội tiếp đường tròn đường kính $CO$ (2)

Từ (1) và (2) $\Rightarrow A,C,M,O$ cùng thuộc một đường tròn có đường kính $CO$ (đpcm).

b) Chứng minh $AC + BD = CD$ và tứ giác $MEOF$ là hình chữ nhật.

+) Xét đường tròn $\left( O \right)$ có $CM$ và $CA$ là hai tiếp tuyến cắt nhau nên $AC = CM$ (tính chất hai tiếp tuyến cắt nhau)

Và $DM$ và $DB$ là hai tiếp tuyến cắt nhau nên $DM = DB$ (tính chất hai tiếp tuyến cắt nhau)

Suy ra $AC + BD = CM + MD = CD$ (đpcm).

+) CM Tứ giác $MEOF$ là hình chữ nhật

Ta có $CM = CA\left( {cmt} \right);\,OM = OA = R$  nên $OC$ là đường trung trực của đoạn $AM \Rightarrow OC \bot AM$ tại $E \Rightarrow \widehat {MEO} = {90^0}.$ (3)

Tương tự ta có $\widehat {MFO} = 90^\circ$   (4)

Xét $\Delta AMB$ nội tiếp đường tròn $\left( O \right)$ có $AB$ là đường kính nên $\Delta MAB$ vuông tại $M$ $\Rightarrow \widehat {EMF} = 90^\circ$  (5)

Từ (3), (4) và (5) $\Rightarrow$ tứ giác $MEOF$ là hình chữ nhật (đpcm).

c) Chứng minh tích $AC.BD$ không đổi khi $M$ di động trên nửa đường tròn.

Do $MEOF$ là hình chữ nhật $\Rightarrow \Delta COD$ vuông tại $O$.

Có $CD$ là tiếp tuyến của $\left( O \right)$ $\Rightarrow MO \bot CD$ tại $M.$

Suy ra $MO$ là đường cao của $\Delta COD$, do đó  $CM.MD = O{M^2} = {R^2}$ (hệ thức lượng trong tam giác vuông)

Từ ý a) ta có $AC = CM;\,\,BD = MD$$\Rightarrow AC.BD = CM.MD = {R^2}$ (không đổi) (đpcm).

d) Tìm vị trí của $M$ trên nửa đường tròn sao cho diện tích tứ giác $ABDC$ nhỏ nhất.

Ta có : $AC,BD$ là tiếp tuyến của $\left( O \right)$ $\Rightarrow AC \bot AB;\,\,\,BD \bot AB$ $\Rightarrow AC//BD$

Do đó: $ABCD$ là hình thang vuông có $AB$ là đường cao.

Khi đó ta có : ${S_{ABCD}} = \frac{1}{2}AB\left( {AC + BD} \right)$ $= \frac{1}{2}AB.CD$ $= \frac{1}{2}AB\left( {AC + BD} \right)\mathop  \ge \limits^{Co - si} \frac{1}{2}AB.2.\sqrt {AC.BD}  = 2{R^2}$

(do theo câu b) ta có $CD = AC + BD$ và theo câu c) ta có$AC.BD = {R^2}$)

Nên $\min {S_{ABCD}} = 2{R^2} \Leftrightarrow CD = AB$ $\Leftrightarrow CD//AB \Leftrightarrow MO \bot AB$ (do $MO \bot CD$)

$\Leftrightarrow M$ là điểm chính giữa của cung $AB.$

Câu 5: (0,5 điểm)

Tìm giá trị lớn nhất của biểu thức: $A = \sqrt {x - 2}  + 2\sqrt {x + 1}  + 2019 - x$.

Phương pháp

Sử dụng hằng đẳng thức ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$

Đưa về dạng $m - {A^2} \le m$

Dấu = xảy ra khi $A = 0.$

Lời giải

Tìm giá trị lớn nhất của biểu thức: $A = \sqrt {x - 2}  + 2\sqrt {x + 1}  + 2019 - x$.

Với điều kiện : $x \ge 2$ ta có:

$2A = 2\left( {\sqrt {x - 2}  + 2\sqrt {x - 1}  + 2019 - x} \right)$

$\Leftrightarrow 2A = 2\sqrt {x - 2}  + 4\sqrt {x - 1}  + 4038 - 2x$

$\Leftrightarrow 2A = 2042 - \left( {x - 2 - 2\sqrt {x - 2}  + 1} \right)$$- \left( {x + 1 - 4\sqrt {x + 1}  + 4} \right)$

$\Leftrightarrow 2A = 4042 - {\left( {\sqrt {x - 2}  - 1} \right)^2} - {\left( {\sqrt {x + 1}  - 2} \right)^2}$

Vì ${\left( {\sqrt {x - 2}  - 1} \right)^2} \ge 0;\,{\left( {\sqrt {x + 1}  - 2} \right)^2} \ge 0\,$ với mọi $x \ge 2$

$\Rightarrow 2A \le 4042 \Rightarrow A \le 2021$

$\Rightarrow \max A = 2021$$\Leftrightarrow \left\{ \begin{array}{l}\sqrt {x - 2}  - 1 = 0\\\sqrt {x + 1}  - 2 = 0\end{array} \right. \Leftrightarrow x = 3$ (thỏa mãn ĐK $x \ge 2$).