Đề kiểm tra học kì 1 Toán 9 - Đề số 23
Đáp án và lời giải chi tiết Đề số 23 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Đề bài
Câu 1: (2 điểm) Tính:
a) \(\left( {3 + \sqrt 8 } \right)\sqrt {17 - 12\sqrt 2 } \)
b)\(\frac{1}{{\sqrt x + 3}} + \frac{1}{{\sqrt x - 3}} - \frac{6}{{x - 9}}\) với x \( \ge \)0; x\( \ne \) 9
Câu 2: ( 1,5 điểm) Cho hai hàm số: \(y\,\, = \,\,\,\frac{1}{2}\,x\) và \(\,y\,\, = \,\,\frac{{ - 1}}{2}x\,\, + \,\,4\) có đồ thị lần lượt là (D 1 ) và (D 2 ).
a) Vẽ (D 1 ) và (D 2 ) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (D 1 ) và (D 2 ) bằng phép toán.
Câu 3: ( 1 điểm) Giải phương trình: \(\sqrt {16x - 48} - 6\sqrt {\frac{{x - 3}}{4}} + \sqrt {4x - 12} = 5\)
Câu 4: ( 1 điểm) Ở siêu thị có thang máy cuốn nhằm giúp khách hàng di chuyển từ tầng này của siêu thị lên tầng kế cận rất tiện lợi. Biết rằng thang cuốn này được thiết kế có độ nghiêng 36 0 so với phương ngang là góc BAH và tốc độ vận hành là 2m/s. Một khách hàng đã di chuyển bằng thang cuốn này từ tầng 1 lên tầng 2 của siêu thị theo hướng AB hết 8 giây. Hỏi khoảng cách giữa tầng 1 và 2 của siêu thị (BH) cao bao nhiêu mét? (Kết quả làm tròn đến chữ số thập phân thứ 2)

Câu 5: ( 0,75 điểm) Tháng 11 vừa qua, có ngày Black Friday (thứ 6 đen – mua sắm siêu giảm giá) , phần lớn các trung tâm thương mại đều giảm giá rất nhiều mặt hàng. Mẹ bạn An có dẫn An đến một trung tâm thương mại để mua một bộ quần áo thể thao. Biết một bộ quần áo thể thao đang khuyến mãi giảm giá 40%, mẹ bạn An có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm, mẹ bạn An chỉ phải trả 684 000 đồng cho một bộ quần áo thể thao. Hỏi giá ban đầu của một bộ quần áo thể thao nếu không khuyến mãi là bao nhiêu?
Câu 6: (0,75điểm) Ước tính dân số Việt Nam được xác định bởi hàm số S = 77,7 + 1,07t trong đó S tính bằng triệu người, t tính bằng số năm kể từ năm 2000.
a) Hãy tính dân số Việt Nam vào các năm 2020 và 2030.
b) Em hãy cho biết dân số Việt Nam đạt 115,15 triệu người vào năm nào?
Câu 7: ( 3 điểm) Cho (O) và điểm I bên ngoài (O). Từ I vẽ một các tuyến IAB với (O). Tiếp tuyến tại A và B cắt nhau tại M. AB cắt OM tại H.
a) Chứng minh: \(M{A^2}\) = MH . MO
b)Từ M kẻ ME vuông góc OI tại E cắt (O) tại D và AB tại K.
Chứng minh: IE . IO = IH . IK
c) Chứng minh: ID là tiếp tuyến (O)
Lời giải
Câu 1: (2 điểm) Tính:
a) \(\left( {3 + \sqrt 8 } \right)\sqrt {17 - 12\sqrt 2 } \)
b)\(\frac{1}{{\sqrt x + 3}} + \frac{1}{{\sqrt x - 3}} - \frac{6}{{x - 9}}\) với x \( \ge \)0; x\( \ne \) 9
Phương pháp
Sử dụng công thức khai phương căn bậc hai, trục căn thức.
Lời giải
a) \(\left( {3 + \sqrt 8 } \right)\sqrt {17 - 12\sqrt 2 } \)
\( = \left( {3 + \sqrt 8 } \right)\sqrt {{{\left( {\sqrt 9 - \sqrt 8 } \right)}^2}} \)
\( = \left( {3 + \sqrt 8 } \right)\left| {3 - \sqrt 8 } \right|\)
\( = {3^2} - {\left( {\sqrt 8 } \right)^2}\)
\( = 1\)
b)\(\frac{1}{{\sqrt x + 3}} + \frac{1}{{\sqrt x - 3}} - \frac{6}{{x - 9}}\)
\( = \frac{{1.(\sqrt x - 3)}}{{(\sqrt x + 3)(\sqrt x - 3)}} + \frac{{1.(\sqrt x + 3)}}{{(\sqrt x - 3)(\sqrt x + 3)}} - \frac{6}{{(\sqrt x - 3)(\sqrt x + 3)}}\)
\(\begin{array}{l} = \frac{{2\sqrt x - 6}}{{(\sqrt x - 3)(\sqrt x + 3)}}\\ = \frac{{2\left( {\sqrt x - 3} \right)}}{{(\sqrt x - 3)(\sqrt x + 3)}}\\ = \frac{2}{{\sqrt x + 3}}\end{array}\)
Câu 2: ( 1,5 điểm) Cho hai hàm số: \(y\,\, = \,\,\,\frac{1}{2}\,x\) và \(\,y\,\, = \,\,\frac{{ - 1}}{2}x\,\, + \,\,4\) có đồ thị lần lượt là (D 1 ) và (D 2 ).
a) Vẽ (D 1 ) và (D 2 ) trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (D 1 ) và (D 2 ) bằng phép toán.
Phương pháp
a) Lấy hai điểm thuộc đồ thị hàm số, ta được đồ thị của hàm số đó.
b) Viết phương trình hoành độ giao điểm của (D 1 ) và (D 2 ). Tìm nghiệm của phương trình. Thay giá trị x tìm được để tìm y.
Lời giải
a) Ta thấy:
+) \(O\left( {0;0} \right){\rm{,A}}\left( {2;1} \right)\) thuộc đồ thị hàm số \(y\,\, = \,\,\,\frac{1}{2}\,x\).
+) \(B\left( {0;4} \right),C\left( {8;0} \right)\) thuộc đồ thị hàm số \(\,y\,\, = \,\,\frac{{ - 1}}{2}x\,\, + \,\,4\).
Từ đó ta có đồ thị của hai hàm số:
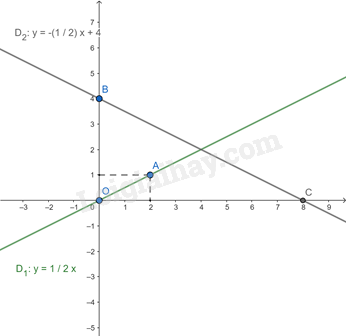
b) Ta có phương trình hoành độ giao điểm của hai đường thẳng (D 1 ) và (D 2 ) là:
\(\begin{array}{l}\,\frac{1}{2}\,x\,\,\, = \,\,\frac{{ - 1}}{2}x\,\, + \,\,4\\\frac{1}{2}x + \frac{1}{2}x = 4\\x = 4\end{array}\)
Với x = 4 ta có \(y = \frac{1}{2}.4 = 2\) ta được điểm \(G\left( {4;2} \right)\).
Vậy giao điểm của (D 1 ) và (D 2 ) là điểm \(G\left( {4;2} \right)\).
Câu 3: ( 1 điểm) Giải phương trình: \(\sqrt {16x - 48} - 6\sqrt {\frac{{x - 3}}{4}} + \sqrt {4x - 12} = 5\)
Phương pháp
Sử dụng công thức khai phương căn bậc hai để có nhân tử chung.
Lời giải
\(\sqrt {16x - 48} - 6\sqrt {\frac{{x - 3}}{4}} + \sqrt {4x - 12} = 5\)
\( \Leftrightarrow \sqrt {16(x - 3)} - 6\sqrt {\frac{{x - 3}}{4}} + \sqrt {4(x - 3)} = 5\) (ĐK: \(x\,\, - \,\,3\,\, \ge \,\,0\,\, \Leftrightarrow \,\,x\,\, \ge \,\,3\))
\( \Leftrightarrow 4\sqrt {x - 3} - 3\sqrt {x - 3} + 2\sqrt {x - 3} = 5\)
\( \Leftrightarrow 3\sqrt {x\,\, - \,\,3} \,\, = \,\,5\)
\( \Leftrightarrow \sqrt {x\,\, - \,\,3} \,\, = \,\,\frac{5}{3}\,\,\)
\( \Leftrightarrow x\,\, - \,\,3\,\, = \,\,\frac{{25}}{9}\,\,\left( {\frac{5}{3} > 0} \right)\)
\( \Leftrightarrow x\, = \,\frac{{52}}{9}\) (TM)
Vậy nghiệm của phương trình là \(x\, = \,\frac{{52}}{9}\).
Câu 4: ( 1 điểm) Ở siêu thị có thang máy cuốn nhằm giúp khách hàng di chuyển từ tầng này của siêu thị lên tầng kế cận rất tiện lợi. Biết rằng thang cuốn này được thiết kế có độ nghiêng 36 0 so với phương ngang là góc BAH và tốc độ vận hành là 2m/s. Một khách hàng đã di chuyển bằng thang cuốn này từ tầng 1 lên tầng 2 của siêu thị theo hướng AB hết 8 giây. Hỏi khoảng cách giữa tầng 1 và 2 của siêu thị (BH) cao bao nhiêu mét? (Kết quả làm tròn đến chữ số thập phân thứ 2)

Phương pháp
Sử dụng tỉ số lượng giác của góc nhọn.
Lời giải
Độ dài AB: AB = 2 x 8 = 16 (m)
Tam giác ABH vuông tại H có \(\sin \widehat {BAH} = \frac{{BH}}{{AB}} \Rightarrow BH = AB.\sin \widehat {BAH} = 16.\sin {36^0} \approx 9,40\left( m \right)\)
Vậy khoảng cách giữa tầng 1 và tầng 2 của siêu thị là khoảng 9,40 m.
Câu 5: ( 0,75 điểm) Tháng 11 vừa qua, có ngày Black Friday (thứ 6 đen – mua sắm siêu giảm giá) , phần lớn các trung tâm thương mại đều giảm giá rất nhiều mặt hàng. Mẹ bạn An có dẫn An đến một trung tâm thương mại để mua một bộ quần áo thể thao. Biết một bộ quần áo thể thao đang khuyến mãi giảm giá 40%, mẹ bạn An có thẻ khách hàng thân thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm, mẹ bạn An chỉ phải trả 684 000 đồng cho một bộ quần áo thể thao. Hỏi giá ban đầu của một bộ quần áo thể thao nếu không khuyến mãi là bao nhiêu?
Phương pháp
Viết phương trình biểu thị giá bộ quần áo.
Lời giải
Gọi x là giá bộ quần áo ban đầu (đồng) x > 684 000 đồng.
Giá bộ quần áo thể thao giảm 40% là: (100% - 40%).x = 60%.x (đồng).
Giá bộ quần áo sau khi giảm thêm 5% trên giá đã giảm là: (100% - 5%). 60%.x = 95%.60%.x = 57%.x
Vì mẹ bạn An phải trả 684 000 đồng cho bộ quần áo => 57%.x = 684 000 nên giá gốc của bộ quần áo đó là:
x = 684 000 : 57% = 1 200 000 (đồng)
Vậy giá ban đầu của một bộ quần áo thể thao nếu không khuyến mãi là 1 200 000 đồng.
Câu 6: (0,75điểm) Ước tính dân số Việt Nam được xác định bởi hàm số S = 77,7 + 1,07t trong đó S tính bằng triệu người, t tính bằng số năm kể từ năm 2000.
a) Hãy tính dân số Việt Nam vào các năm 2020 và 2030.
b) Em hãy cho biết dân số Việt Nam đạt 115,15 triệu người vào năm nào?
Phương pháp
a) Lấy 2020 và 2030 trừ 2000 để tính số năm kể từ năm 2000. Thay số năm t vào hàm số S = 77,7 +1,07t để tính dân số Việt Nam năm 2020 và 2030.
b) Thay S = 115,15 vào hàm số để tính năm. Lấy 2000 cộng với số năm để tính được năm số dân Việt Nam đạt 115,15 triệu người.
Lời giải
a) Dân số Việt Nam vào năm 2020
S = 77,7 + 1,07(2020 – 2000) = 99,1 (triệu người)
Dân số Việt Nam vào các năm 2030
S = 77,7 + 1,07(2030 – 2000) = 109,8 (triệu người)
b) Dân số Việt Nam đạt 115,15 triệu người tức là S = 115,15.
Thay S = 115,15 vào hàm số, ta có: 77,7 + 1,07t = 115,15 \( \Leftrightarrow \) t = 35.
Vậy dân số Việt Nam đạt 115,15 triệu người vào năm 2000 + 35 = 2035.
Câu 7: ( 3 điểm) Cho (O) và điểm I bên ngoài (O). Từ I vẽ một các tuyến IAB với (O). Tiếp tuyến tại A và B cắt nhau tại M. AB cắt OM tại H.
a) Chứng minh: \(M{A^2}\) = MH . MO
b) Từ M kẻ ME vuông góc OI tại E cắt (O) tại D và AB tại K.
Chứng minh: IE . IO = IH . IK
c) Chứng minh: ID là tiếp tuyến (O)
Phương pháp
a) Sử dụng hệ thức lượng để chứng minh.
b) Chứng minh (g.g)
c) Chứng minh OD vuông góc với ID và D thuộc (O).
Lời giải
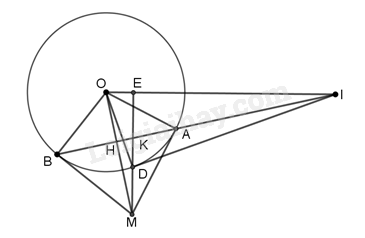
a) Ta có \(MA\), \(MB\) là hai tiếp tuyến của \((0)\) cắt nhau tại \(M\).
Suy ra \(MA = MB\).
Khi đó \(M\) nằm trên đường trung trực của đoạn thẳng \(AB\)
Lại có \(OA = OB = R\).
Suy ra \(O\) nằm trên đường trung trực của đoạn thẳng \(AB\) (2)
Từ (1), (2), suy ra \(MO\) là đường trung trực của đoạn thẳng \(AB\).
Do đó \(MO \bot AB\) tại \(H\) và \(H\) là trung điểm AB.
Ta có MA là tiếp tuyến của \((O)\).
Suy ra \(\widehat {AOM} = {90^0}\).
Xét \(\Delta AOM\) vuông tại \(A\) có \(AH\) là đường cao:
\(M{A^2} = MH \cdot MO\) (hệ thức lượng trong tam giác vuông).
b) Xét \(\Delta IEK\) và \(\Delta IHO\), có:
\(\widehat {IEK} = \widehat {IHO} = {90^0}{\rm{. }}\)
\(\hat I\) chung.
Do đó $\Delta IEK \backsim \Delta IHO$ (g.g).
Suy ra \(\frac{{IE}}{{IH}} = \frac{{IK}}{{IO}}\).
Do đó IE.IO = IH.IK.
c) Xét \(\Delta OEM\) và \(\Delta OHI\), có:
\(\widehat {OEM} = \widehat {OHI} = {90^0}{\rm{. }}\)
\(\hat O\) chung.
Do đó $\Delta OEM \backsim \Delta OHI$ (g.g).
Suy ra \(\frac{{OE}}{{OH}} = \frac{{OM}}{{OI}}\).
Do đó \(OE.OI = OM.OH\).
Xét \(\Delta AOM\) vuông tại \(A\) có \(AH\) là đường cao:
\(O{A^2} = OH.OM\) (hệ thức lượng trong tam giác vuông).
Suy ra OE.OI \( = O{A^2}\).
Mà \(OA = OD = R\).
Do đó OE.OI = OD² .
Xét \(\Delta ODI\) và \(\Delta OED\), có:
\(\frac{{OD}}{{OE}} = \frac{{OI}}{{OD}}\left( {OE \cdot OI = O{D^2}} \right){\rm{. }}\)
\(\hat O\) chung.
Do đó $\Delta O D I \backsim \Delta O E D$ (c.g.c).
Suy ra \(\widehat {ODI} = \widehat {OED} = {90^0}\).
Do đó \(OD \bot DI\).
Vậy ID là tiếp tuyến của (0).