Đề kiểm tra học kì 1 Toán 9 - Đề số 21
Đáp án và lời giải chi tiết Đề số 21 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Đề bài
Câu 1: (2 điểm) Tính:
a) \(2\sqrt {128} + \sqrt {162} - \sqrt {200} - 6\sqrt {98} \)
b) \(\frac{{\sqrt a }}{{\sqrt a - \sqrt b }} - \frac{{\sqrt b }}{{\sqrt a + \sqrt b }} - \frac{{2b}}{{a - b}}\) với \(a \ge 0,b \ge 0,a \ne b\)
Câu 2: ( 1,5 điểm) Cho hàm số\(\;y = \frac{1}{2}x - 2\;\)có đồ thị (d) và hàm số y = -2x +3 có đồ thị (d’)
a) Vẽ (d) và (d’) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (d) và (d’) bằng phép tính.
Câu 3: ( 1 điểm) Giải phương trình: \(\sqrt {9x - 18} + 5\sqrt {4x - 8} = \sqrt {x - 2} + 3\)
Câu 4: ( 1 điểm) Từ đỉnh một ngọn đèn biển cao 35m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới góc 30 0 so với đường thẳng nằm ngang chân đèn (hình bên dưới). Hỏi khoảng cách từ đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu?
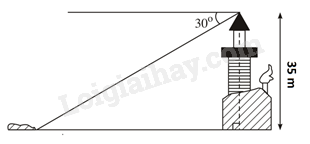
Câu 5: ( 0,75 điểm) Quãng đường của một chiếc xe chạy từ A đến B cách nhau 235km được xác định bởi hàm số s = 50t + 10 , trong đó s (km) là quãng đường của xe chạy được, và t (giờ) là thời gian đi của xe.
a) Hỏi sau 3 giờ xuất phát thì xe cách B bao nhiêu km?
b) Thời gian xe chạy hết quãng đường AB là bao nhiêu giờ ?
Câu 6: (0,75điểm) Bạn An ra nhà sách và mang theo một số tiền vừa đủ để mua 10 quyển tập
và 6 cây bút. Nhưng khi ra đến nơi, giá một quyển tập mà bạn An định mua đã tăng lên 500 đồng một quyển tập, còn giá một cây bút thì giảm 1000 đồng một cây so với dự định. Vậy để mua 10 quyển tập và 6 cây bút như trên thì bạn An còn thừa hay thiếu số tiền là bao nhiêu?
Câu 7: ( 3 điểm) Cho nửa đường tròn (O; R) có đường kính AB. Tiếp tuyến tại điểm M trên nửa đường tròn lần lượt cắt hai tiếp tuyến tại A và B ở C và D.
a) Chứng minh : AC + DB = CD.
b) Chứng minh : tam giác COD vuông và AC.BD = R 2 .
c) Chứng minh : AB là tiếp tuyến của đường tròn có đường kính CD.
-------- Hết --------
Lời giải
Câu 1: (2 điểm) Tính:
a) \(2\sqrt {128} + \sqrt {162} - \sqrt {200} - 6\sqrt {98} \)
b) \(\frac{{\sqrt a }}{{\sqrt a - \sqrt b }} - \frac{{\sqrt b }}{{\sqrt a + \sqrt b }} - \frac{{2b}}{{a - b}}\) với \(a \ge 0,b \ge 0,a \ne b\)
Phương pháp
Sử dụng công thức khai phương căn bậc hai, trục căn thức.
Lời giải
a) \(2\sqrt {128} + \sqrt {162} - \sqrt {200} - 6\sqrt {98} \)
\( = 2\sqrt {64.2} + \sqrt {81.2} - \sqrt {100.2} - 6\sqrt {49.2} \)
\( = 16\sqrt 2 + 9\sqrt 2 - 10\sqrt 2 - 42\sqrt 2 \)
\( = - 27\sqrt 2 \)
b) \(\frac{{\sqrt a }}{{\sqrt a - \sqrt b }} - \frac{{\sqrt b }}{{\sqrt a + \sqrt b }} - \frac{{2b}}{{a - b}}\) với \(a \ge 0,b \ge 0,a \ne b\)
\( = \frac{{\sqrt a \left( {\sqrt a + \sqrt b } \right)}}{{{{\sqrt a }^2} - {{\sqrt b }^2}}} - \frac{{\sqrt b \left( {\sqrt a - \sqrt b } \right)}}{{{{\sqrt a }^2} - {{\sqrt b }^2}}} - \frac{{2b}}{{a - b}}\)
\( = \frac{{a + \sqrt {ab} - \sqrt {ab} + b}}{{a - b}} - \frac{{2b}}{{a - b}}\)
\( = \frac{{a + b}}{{a - b}} - \frac{{2b}}{{a - b}}\)
\( = \frac{{a - b}}{{a - b}}\)
= 1
Câu 2: ( 1,5 điểm) Cho hàm số\(\;y = \frac{1}{2}x - 2\;\)có đồ thị (d) và hàm số y = -2x +3 có đồ thị (d’)
a) Vẽ (d) và (d’) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (d) và (d’) bằng phép tính.
Phương pháp
a) Lấy hai điểm thuộc đồ thị hàm số, ta được đồ thị của hàm số đó.
b) Viết phương trình hoành độ giao điểm của (d) và (d’). Tìm nghiệm của phương trình. Thay giá trị x tìm được để tìm y.
Lời giải
a) Ta thấy:
+) \(A\left( {0; - 2} \right),B\left( {4;0} \right)\) thuộc đồ thị hàm số \(\;y = \frac{1}{2}x - 2\;\).
+) \(C\left( {0;3} \right),D\left( {\frac{3}{2};0} \right)\) thuộc đồ thị hàm số y = -2x +3.
Từ đó ta có đồ thị của hai hàm số:
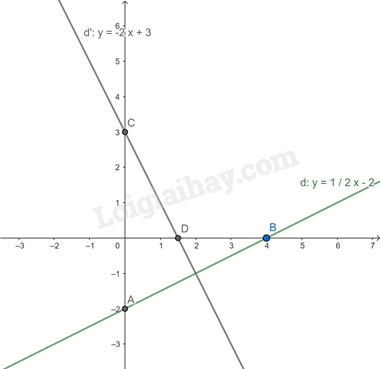
b) Ta có phương trình hoành độ giao điểm của hai đường thẳng (d) và (d’) là:
\(\begin{array}{l}\frac{1}{2}x - 2 = - 2x + 3\\ \Leftrightarrow \frac{1}{2}x + 2x = 3 + 2\\ \Leftrightarrow \frac{5}{2}x = 5\\ \Leftrightarrow x = 2\end{array}\)
Với x = 2 ta có \(y = - 2.2 + 3 = - 1\) ta được điểm G(2;-1)
Vậy giao điểm của (d) và (d’) là điểm G(2;-1).
Câu 3: ( 1 điểm) Giải phương trình: \(\sqrt {9x - 18} + 5\sqrt {4x - 8} = \sqrt {x - 2} + 3\)
Phương pháp
Sử dụng công thức khai phương căn bậc hai để có nhân tử chung.
Lời giải
\(\sqrt {9x - 18} + 5\sqrt {4x - 8} = \sqrt {x - 2} + 3\) (ĐK: \(x \ge 2\))
\( \Leftrightarrow \)\(\sqrt {9\left( {x - 2} \right)} + 5\sqrt {4\left( {x - 2} \right)} - \sqrt {x - 2} = 3\)
\( \Leftrightarrow \)\(12\sqrt {x - 2} = 3\)
\( \Leftrightarrow \)\(\sqrt {x - 2} = \frac{1}{4}\)
\( \Leftrightarrow \)\(x = \frac{{33}}{{16}}\) (TM)
Vậy nghiệm của phương trình là \(x = \frac{{33}}{{16}}\).
Câu 4: ( 1 điểm) Từ đỉnh một ngọn đèn biển cao 35m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới góc 30 0 so với đường thẳng nằm ngang chân đèn (hình bên dưới). Hỏi khoảng cách từ đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu?
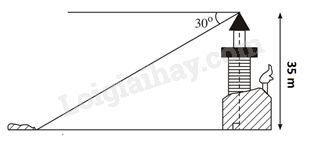
Phương pháp
Sử dụng tính chất của hai đường thẳng song song.
Sử dụng tỉ số lượng giác của góc nhọn.
Lời giải
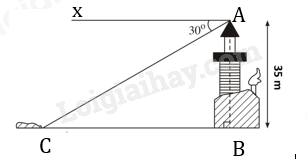
Ta có: \(\widehat {xAC} = \widehat {ACB}\) (hai góc so le trong).
Xét tam giác ABC vuông tại B, ta có: \(\tan C = \frac{{AB}}{{BC}}\)\( \Leftrightarrow \tan {30^0} = \frac{{35}}{{BC}}\)
\( \Rightarrow BC = 35:\tan {30^0} \approx 60,6\left( m \right)\).
Vậy khoảng cách từ đảo đến chân đèn (ở mực nước biển) khoảng 60,6m.
Câu 5: ( 0,75 điểm) Quãng đường của một chiếc xe chạy từ A đến B cách nhau 235km được xác định bởi hàm số s = 50t + 10 , trong đó s (km) là quãng đường của xe chạy được, và t (giờ) là thời gian đi của xe.
a) Hỏi sau 3 giờ xuất phát thì xe cách B bao nhiêu km?
b) Thời gian xe chạy hết quãng đường AB là bao nhiêu giờ ?
Phương pháp
a) Thay t = 3 vào hàm số để tính quãng đường xe chay được sau 3 giờ. Khoảng cách của xe với B sau 3 giờ bằng quãng đường AB – quãng đường xe đã đi.
b) Thay s = 235 để tính thời gian xe chạy hết quãng đường AB.
Lời giải
a) Quãng đường đi được sau 3 giờ : s = 50.3 + 10 = 160 (km)
Sau 3 giờ xuất phát thì xe cách B: 235 – 160 = 75 (km)
b) Xe chạy hết quãng đường AB thì s = 235.
Thay s = 235 vào hàm số s = 50t + 10, ta có phương trình: 235 = 50t + 10 \( \Rightarrow \) t = 4,5(giờ). Vậy thời gian xe đi hết quãng đường AB là 4,5 giờ.
Câu 6: (0,75điểm) Bạn An ra nhà sách và mang theo một số tiền vừa đủ để mua 10 quyển tập và 6 cây bút. Nhưng khi ra đến nơi, giá một quyển tập mà bạn An định mua đã tăng lên 500 đồng một quyển tập, còn giá một cây bút thì giảm 1000 đồng một cây so với dự định. Vậy để mua 10 quyển tập và 6 cây bút như trên thì bạn An còn thừa hay thiếu số tiền là bao nhiêu?
Phương pháp
Gọi giá tiền 1 quyển tập là x, 1 cây bút là y.
Viết phương trình biểu thị số tiền mua tập và bút theo dự kiến và thực tế.
Biểu thị số số tiền thực tế theo số tiền dự định.
Lời giải
Gọi giá tiền 1 quyển tập là x, giá tiền 1cây bút là y (\(x,y \in N*,x > 0;y > 1000\))
Số tiền mua tập và bút theo dự định là: \({T_1} = 10x + 6y\)
Số tiền mua tập và bút trên thực tế là:
T 2 = 10(x + 500) + 6(y – 1000)
= 10x + 5000+ 6y – 6000
= 10x + 6y – 1000
= T 1 – 1000
Vậy bạn An còn thừa 1000 đồng.
Câu 7: ( 3 điểm) Cho nửa đường tròn (O; R) có đường kính AB. Tiếp tuyến tại điểm M trên nửa đường tròn lần lượt cắt hai tiếp tuyến tại A và B ở C và D.
a) Chứng minh : AC + DB = CD.
b) Chứng minh : tam giác COD vuông và AC.BD = R 2 .
c) Chứng minh : AB là tiếp tuyến của đường tròn có đường kính CD.
Phương pháp
a) Sử dụng tính chất của hai tiếp tuyến cắt nhau.
b) Chứng minh CO và OD là 2 tia phân giác của 2 góc kề bù.
c) Gọi I là trung điểm của CD, chứng minh OI vuông góc với AB tại O nên AB là tiếp tuyến của đường tròn có đường kính CD.
Lời giải
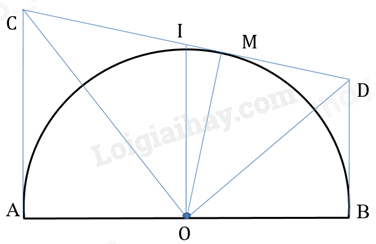
a) Ta có: CD = CM + MD
Mà: CM = CA (tính chất hai tiếp tuyến cắt nhau)
MD = DB (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \) CD = CA + DB (đpcm)
b) Ta có: \(\widehat {CAB} = \widehat {DBA} = {90^0} \Rightarrow AC//BD\) nên ABDC là hình thang vuông nên \(\widehat C + \widehat D = {180^0}\).
Xét tam giác ACO và tam giác MCO có:
AC = MC
\(\widehat {CAO} = \widehat {CMO} = {90^0}\) (CA và CM là tiếp tuyến của (O; R))
AO = OM = R
\( \Rightarrow \Delta ACO = \Delta MCO\left( {c.g.c} \right)\)
\( \Rightarrow \widehat {ACO} = \widehat {MCO} = \frac{1}{2}\widehat {ACD}\)(hai góc tương ứng) (1)
Chứng minh tương tự, ta có: \(\Delta BDO = \Delta MDO\left( {c.g.c} \right) \Rightarrow \widehat {BDO} = \widehat {MDO} = \frac{1}{2}\widehat {BDM}\)(2)
Từ (1) và (2) suy ra: \(\widehat {MCO} + \widehat {MDO} = \frac{1}{2}\left( {\widehat {ACD} + \widehat {BDM}} \right) = \frac{1}{2}{.180^0} = {90^0}\)
Xét tam giác COD có \(\widehat {MCO} + \widehat {MDO} = {90^0} \Rightarrow \widehat {COD} = {180^0} - {90^0} = {90^0}\) hay tam giác COD vuông tại O (đpcm)
Xét tam giác vuông COD có OM là đường cao nên CM.MD = OM 2 = R 2 .
Mà CM = CA; MD = DB suy ra CA.DB = R 2 (đpcm)
c) Gọi I là trung điểm của CD suy ra I là tâm đường tròn ngoại tiếp \(\Delta \)COD đường kính CD.
\( \Rightarrow \) OI là đường trung bình của hình thang ABDC.
\( \Rightarrow \) OI // AC.
Mà AC \( \bot \) AB nên OI \( \bot \) AB tại O hay AB là tiếp tuyến của đường tròn đường kính CD.