Đề kiểm tra học kì 1 Toán 9 - Đề số 26 — Không quảng cáo

Đề bài

Câu 1: (2,5 điểm):

Cho hai biểu thức $A = \frac{{\sqrt x  - 2}}{{\sqrt x  + 3}}$ và $B = \frac{{2\sqrt x }}{{\sqrt x  + 2}} + \frac{9}{{\sqrt x  - 2}} + \frac{{\sqrt x  + 18}}{{4 - x}}$ (với $x \ge 0,x \ne 4$)

a) Tính giá trị của biểu thức $A$ khi $x = 9$.

b) Chứng minh rằng: $B = \frac{{2\sqrt x }}{{\sqrt x  - 2}}$

c) Tìm giá trị của $x$ để $P = A.B$ có giá trị nguyên lớn nhất.

Câu 2: (2,0 điểm)

1) Giải phương trình: $\sqrt {x - 1}  + \sqrt {9x - 9}  - \frac{1}{2}\sqrt {4x - 4}  = \frac{1}{2}$

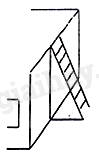
2) Để lên sân thượng của ngôi nhà một tầng cao 3,5m người ta dùng một chiếc thang dài 4m được đặt như hình vẽ. Hỏi cách đặt thang như vậy đã đảm bảo an toàn chưa? Biết thang ở vị trí an toàn cho người dùng khi thang tạo với mặt đất có độ lớn từ ${60^0}$ đến ${75^0}$.

Câu 3: (2,0 điểm)

Cho hàm số bậc nhất $y = \left( {m + 1} \right)x - 2$ có đồ thị là đường thẳng $\left( d \right)$. Trong đó $m$ là tham số, $m \ne  - 1$.

1) Vẽ đồ thị hàm số và tính khoảng cách từ gốc tọa độ đến đồ thị hàm số với $m = 1$ (đơn vị đo trên các trục tọa độ là cm).

2) Tìm giá trị của $m$ để đồ thị hàm số đã cho cắt đồ thị hàm số $y = x - 1$ tại một điểm có hoành độ là 3.

Câu 4: (3,0 điểm)

Cho đường tròn tâm $O$, bán kính $R$ và một điểm $A$ ở ngoài đường tròn sao cho $OA = 2R$. Qua điểm $A$ kẻ tiếp tuyến $AB$ với đường tròn $O(B$ là tiếp điểm). Qua điểm $B$ kẻ $BH$ vuông góc với $OA\left( {H \in OA} \right)$, $BH$ kéo dài cắt đường tròn tâm $O$ tại điểm thứ hai là $C$.

1) Tính $AB$ và $BH$ nếu $R = 2cm$

2) Chứng minh rằng: 4 điểm $A,B,O,C$ cùng thuộc một đường tròn.

3) Tia đối của tia $OA$ cắt đường tròn tâm $O$ tại $M$. Chứng minh rằng: $MB$ là tiếp tuyến của đường tròn đường kính $OA$.

Câu 5: (0,5 điểm) Giải phương trình: $\sqrt {x - 3}  + \sqrt {5 - x}  = 2{x^2} - 16x + 34$

-------- Hết --------

Lời giải

Câu 1: (2,5 điểm):

Cho hai biểu thức $A = \frac{{\sqrt x  - 2}}{{\sqrt x  + 3}}$ và $B = \frac{{2\sqrt x }}{{\sqrt x  + 2}} + \frac{9}{{\sqrt x  - 2}} + \frac{{\sqrt x  + 18}}{{4 - x}}$ (với $x \ge 0,x \ne 4$)

a) Tính giá trị của biểu thức $A$ khi $x = 9$.

b) Chứng minh rằng: $B = \frac{{2\sqrt x }}{{\sqrt x  - 2}}$

c) Tìm giá trị của $x$ để $P = A.B$ có giá trị nguyên lớn nhất.

Phương pháp

a) Với $x = 9$ (tmđk) thay vào $A$ và tính.

b) Xác định mẫu thức chung

Thực hiện các phép tính với phân thức đại số

c) Sử dụng phương pháp miền giá trị, xác định miền chặn của $P$, từ đó tìm các giá trị $x$ thỏa mãn

Lời giải

a) Với $x = 9$ (tmđk) thay vào $A$, ta được: $A = \frac{{\sqrt 9  - 2}}{{\sqrt 9  + 3}} = \frac{{3 - 2}}{{3 + 3}} = \frac{1}{6}$

Vậy $x = 9$ thì $A = \frac{1}{6}$

b) $B = \frac{{2\sqrt x }}{{\sqrt x  + 2}} + \frac{9}{{\sqrt x  - 2}} + \frac{{\sqrt x  + 18}}{{4 - x}}$

$\begin{array}{l}B = \frac{{2\sqrt x }}{{\sqrt x  + 2}} + \frac{9}{{\sqrt x  - 2}} - \frac{{\sqrt x  + 18}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\B = \frac{{2\sqrt x \left( {\sqrt x  - 2} \right) + 9\left( {\sqrt x  + 2} \right) - \left( {\sqrt x  + 18} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\B = \frac{{2x - 4\sqrt x  + 9\sqrt x  + 18 - \sqrt x  - 18}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\B = \frac{{2x + 4\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\B = \frac{{2\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\B = \frac{{2\sqrt x }}{{\sqrt x  - 2}}\end{array}$

Vậy $B = \frac{{2\sqrt x }}{{\sqrt x  - 2}}$ với $x \ge 0,x \ne 4$

c) Ta có: $P = A.B = \frac{{\sqrt x  - 2}}{{\sqrt x  + 3}}.\frac{{2\sqrt x }}{{\sqrt x  - 2}} = \frac{{2\sqrt x }}{{\sqrt x  + 3}}$

$= \frac{{2\left( {\sqrt x  + 3} \right) - 6}}{{\sqrt x  + 3}} = 2 - \frac{6}{{\sqrt x  + 3}}$

Vì $x \ge 0,x \ne 4 \Rightarrow P = \frac{{2\sqrt x }}{{\sqrt x  + 3}} \ge 0$

Mặt khác, khi $x \ge 0,x \ne 4$ có: $P = 2 - \frac{6}{{\sqrt x  + 3}} < 2$

Suy ra $0 \le P < 2$ mà $P$ nguyên lớn nhất $\Leftrightarrow P = 1$

$\begin{array}{l} \Leftrightarrow \frac{{2\sqrt x }}{{\sqrt x  + 3}} = 1\\ \Rightarrow \sqrt x  + 3 = 2\sqrt x \\ \Leftrightarrow \sqrt x  = 3\\ \Leftrightarrow x = 9\left( {tmdk} \right)\end{array}$

Vậy $x = 9$ thì $P = A.B$ có giá trị nguyên lớn nhất.

Câu 2: (2,0 điểm)

1) Giải phương trình: $\sqrt {x - 1}  + \sqrt {9x - 9}  - \frac{1}{2}\sqrt {4x - 4}  = \frac{1}{2}$

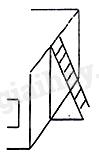
2) Để lên sân thượng của ngôi nhà một tầng cao 3,5m người ta dùng một chiếc thang dài 4m được đặt như hình vẽ. Hỏi cách đặt thang như vậy đã đảm bảo an toàn chưa? Biết thang ở vị trí an toàn cho người dùng khi thang tạo với mặt đất có độ lớn từ ${60^0}$ đến ${75^0}$.

Phương pháp

1) Biểu thức $\sqrt {f\left( x \right)}$ xác định $\Leftrightarrow f\left( x \right) \ge 0$

Giải phương trình: $\sqrt {f\left( x \right)}  = a\left( {a \ge 0} \right) \Leftrightarrow f\left( x \right) = {a^2}$

Lời giải

1) ĐKXĐ: $x \ge 1$

$\begin{array}{l}\,\,\,\,\,\,\,\,\sqrt {x - 1}  + \sqrt {9x - 9}  - \frac{1}{2}\sqrt {4x - 4}  = \frac{1}{2}\\ \Leftrightarrow \sqrt {x - 1}  + \sqrt {9\left( {x - 1} \right)}  - \frac{1}{2}\sqrt {4\left( {x - 1} \right)}  = \frac{1}{2}\\ \Leftrightarrow \sqrt {x - 1}  + 3\sqrt {x - 1}  - \frac{1}{2}.2\sqrt {x - 1}  = \frac{1}{2}\\ \Leftrightarrow \left( {1 + 3 - 1} \right)\sqrt {x - 1}  = \frac{1}{2}\\ \Leftrightarrow 3\sqrt {x - 1}  = \frac{1}{2}\\ \Leftrightarrow \sqrt {x - 1}  = \frac{1}{6}\\ \Leftrightarrow x - 1 = \frac{1}{{36}}\\ \Leftrightarrow x = \frac{{37}}{{36}}\,\,\left( {tmdk} \right)\end{array}$

Vậy phương trình có tập nghiệm là $S = \left\{ {\frac{{37}}{{36}}} \right\}$

2) Gọi tên các điểm như hình vẽ bên.

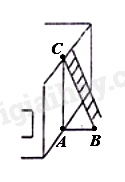
$\Delta ABC$ vuông tại $A$, áp dụng hệ thức lượng trong tam giác vuông, ta có;

$\begin{array}{l}\sin \angle ABC = \frac{{AC}}{{BC}} = \frac{{3,5}}{4} = \frac{7}{8}\\ \Rightarrow \angle ABC \approx {61^0}\end{array}$

$\Rightarrow$ Thang được đặt ở vị trí an toàn cho người dùng.

Câu 3: (2,0 điểm)

Cho hàm số bậc nhất $y = \left( {m + 1} \right)x - 2$ có đồ thị là đường thẳng $\left( d \right)$. Trong đó $m$ là tham số, $m \ne  - 1$.

1) Vẽ đồ thị hàm số và tính khoảng cách từ gốc tọa độ đến đồ thị hàm số với $m = 1$ (đơn vị đo trên các trục tọa độ là cm).

2) Tìm giá trị của $m$ để đồ thị hàm số đã cho cắt đồ thị hàm số $y = x - 1$ tại một điểm có hoành độ là 3.

Phương pháp

1) * Vẽ đồ thị của hàm số $y = ax + b$

+ Lập bảng giá trị tương ứng của $x$ và $y$

+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.

* Gọi giao điểm của đường thẳng với trục $Ox,Oy$ là $A,B$

Kẻ $OH$ vuông góc với đường thẳng $y = 2x - 2$

Tính $OH$: $\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}$

2) Thay $x = 3$ vào hàm số $y = x - 1$, tìm được tọa độ giao điểm

Thay tọa độ giao điểm vừa tìm được vào hàm số $y = \left( {m + 1} \right)x - 2$, tìm được tham số $m$

Lời giải

1) Với $m = 1$, ta có: $y = 2x - 2$

Ta có bảng giá trị của $x$ và $y$:

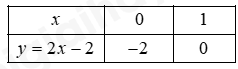
Đồ thị hàm số đi qua các điểm $A\left( {1;0} \right);B\left( {0; - 2} \right)$

Vẽ đồ thị:

* Kẻ $OH$ vuông góc với đường thẳng $y = 2x - 2$

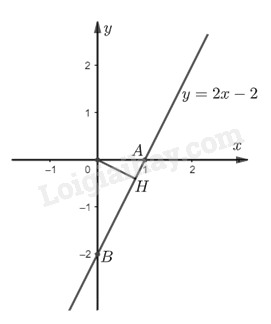
Gọi $A\left( {1;0} \right)$, $B\left( {0; - 2} \right)$ là giao điểm của $Ox,Oy$ với đường thẳng $y = 2x - 2$

Khi đó, $OA = \left| 1 \right| = 1;OB = \left| { - 2} \right| = 2$

$\Delta OAB$ vuông tại $O,OH \bot AB$, áp dụng hệ thức lượng trong tam giác vuông, ta có:

$\begin{array}{l}\,\,\,\,\,\,\,\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\\ \Leftrightarrow \frac{1}{{O{H^2}}} = \frac{1}{1} + \frac{1}{{{2^2}}}\\ \Leftrightarrow \frac{1}{{O{H^2}}} = \frac{5}{4}\\ \Rightarrow OH = \frac{{2\sqrt 5 }}{5}\left( {cm} \right)\end{array}$

Vậy khoảng cách từ $O$ đến đường thẳng $y = 2x - 2$ bằng $\frac{{2\sqrt 5 }}{5}cm$

2) Với $x = 3$ thay vào $y = x - 1$, ta được: $y = 3 - 1 = 2$

$\Rightarrow$ Giao điểm của $\left( d \right)$ và đường thẳng $y = x - 1$ có tọa độ $I\left( {3;2} \right)$

Vì $I \in \left( d \right)$ nên ta có: $3\left( {m + 1} \right) - 2 = 2 \Leftrightarrow m + 1 = \frac{4}{3} \Leftrightarrow m = \frac{1}{3}$

Vậy $m = \frac{1}{3}$ .

Câu 4: (3,0 điểm)

Cho đường tròn tâm $O$, bán kính $R$ và một điểm $A$ ở ngoài đường tròn sao cho $OA = 2R$. Qua điểm $A$ kẻ tiếp tuyến $AB$ với đường tròn $O(B$ là tiếp điểm). Qua điểm $B$ kẻ $BH$ vuông góc với $OA\left( {H \in OA} \right)$, $BH$ kéo dài cắt đường tròn tâm $O$ tại điểm thứ hai là $C$.

1) Tính $AB$ và $BH$ nếu $R = 2cm$

2) Chứng minh rằng: 4 điểm $A,B,O,C$ cùng thuộc một đường tròn.

3) Tia đối của tia $OA$ cắt đường tròn tâm $O$ tại $M$. Chứng minh rằng: $MB$ là tiếp tuyến của đường tròn đường kính $OA$.

Phương pháp

1) Vận dụng định lý Py – ta – go, tính $AB$

Áp dụng hệ thức lượng trong tam giác vuông, tính $BH$

2) $B,C$ cùng thuộc đường tròn đường kính $AO$

3) $I \in \left( O \right)$ và $IB \bot BM \Rightarrow BM$ là tiếp tuyến của đường tròn đường kính $OA$

Lời giải

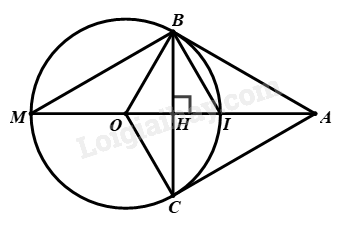
1) $AB$ là tiếp tuyến của đường tròn $\left( O \right)$ tại $B$$\Rightarrow \angle ABO = {90^0}$ (tính chất tiếp tuyến của đường tròn)

$\Rightarrow \Delta OAB$ vuông tại $B$

$\Delta OAB$ vuông tại $B$, áp dụng định lý Py – ta – go, ta có:

$\begin{array}{l}\,\,\,\,\,\,\,\,\,O{A^2} = A{B^2} + O{B^2}\\ \Leftrightarrow A{B^2} = O{A^2} - O{B^2}\\ \Leftrightarrow A{B^2} = {4^2} - {2^2}\\ \Leftrightarrow A{B^2} = 12\\ \Rightarrow AB = 2\sqrt 3 \end{array}$

$\Delta OAB$ vuông tại $B,BH \bot OA$, áp dụng hệ thức lượng trong tam giác vuông, ta có:

$\begin{array}{l}\,\,\,\,\,\,\,\,\frac{1}{{B{H^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{A{B^2}}}\\ \Leftrightarrow \frac{1}{{B{H^2}}} = \frac{1}{{{2^2}}} + \frac{1}{{{{\left( {2\sqrt 3 } \right)}^2}}}\\ \Leftrightarrow \frac{1}{{B{H^2}}} = \frac{1}{3}\\ \Rightarrow BH = \sqrt 3 \left( {cm} \right)\end{array}$

2) $\Delta OBC$ cân tại $B\left( {do\,\,\,OB = OC = R} \right)$ có $OH$ là đường cao (do $OH \bot BC$)

$\Rightarrow OH$ là đường phân giác của $\angle BOC \Rightarrow \angle BOH = \angle HOC$

Xét $\Delta AOB$ và $\Delta AOC$ có:

$\left. \begin{array}{l}OB = OC = R\\\angle BOA = \angle COA\left( {cmt} \right)\\OA\,\,chung\end{array} \right\} \Rightarrow \Delta AOB = \Delta AOC\left( {c.g.c} \right) \Rightarrow \angle ABO = \angle ACO$ (hai góc tương ứng)

Mà $\angle ABO = {90^0} \Rightarrow \angle ACO = {90^0}$

$\Rightarrow \Delta AOC$ vuông tại $C$

$\Rightarrow C$ thuộc đường tròn đường kính $AO$

$\Delta ABO$ vuông tại $B$

$\Rightarrow B$ thuộc đường tròn đường kính $AO$

Vậy $B,C$ cùng thuộc đường tròn đường kính $AO$ nên bốn điểm $A,B,O,C$ cùng thuộc một đường tròn.

3) Gọi $I$ là trung điểm của $OA \Rightarrow OI = IA = \frac{1}{2}OA = R$

$\Rightarrow I \in \left( O \right)$

Mặt khác, $I$ là tâm của đường tròn đường kính $OA$

Ta có: $B$ thuộc đường tròn đường kính $MI \Rightarrow \angle IBM = {90^0} \Rightarrow MB \bot BI$

Mà $I$ là tâm của đường tròn đường kính $OA$

$\Rightarrow BM$ là tiếp tuyến của đường tròn đường kính $OA$

Câu 5: (0,5 điểm) Giải phương trình: $\sqrt {x - 3}  + \sqrt {5 - x}  = 2{x^2} - 16x + 34$

Phương pháp

Sử dụng bất đẳng thức bunhiacopxki đánh giá vế phải, sử dụng hằng đẳng thức đánh giá vế trái

Dấu bằng xảy ra và tìm nghiệm của phương trình

Lời giải

ĐKXĐ: $3 \le x \le 5$

Áp dụng bất đẳng thức Bunhiacopxki ta có:

${\left( {1.\sqrt {x - 3}  + 1.\sqrt {5 - x} } \right)^2} \le \left( {{1^2} + {1^2}} \right)\left[ {{{\left( {\sqrt {x - 3} } \right)}^2} + {{\left( {\sqrt {5 - x} } \right)}^2}} \right]$

$\begin{array}{l} \Leftrightarrow {\left( {\sqrt {x - 3}  + \sqrt {5 - x} } \right)^2} \le 2.\left( {x - 3 + 5 - x} \right)\\ \Leftrightarrow {\left( {\sqrt {x - 3}  + \sqrt {5 - x} } \right)^2} \le 4\\ \Leftrightarrow 0 \le \sqrt {x - 3}  + \sqrt {5 - x}  \le 2\\ \Leftrightarrow 0 \le VT \le 2\end{array}$

Ta có: $2{x^2} - 16x + 34 = 2\left( {{x^2} - 8x + 16} \right) + 2 = 2{\left( {x - 4} \right)^2} + 2$

Vì ${\left( {x - 4} \right)^2} \ge 0,\forall x$

$\begin{array}{l} \Rightarrow 2{\left( {x - 4} \right)^2} + 2 \ge 2,\forall x\\ \Rightarrow VP \ge 2\end{array}$

Dấu “=” xảy ra $\Leftrightarrow \left\{ \begin{array}{l}\sqrt {x - 3}  = \sqrt {5 - x} \\{\left( {x - 4} \right)^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3 = 5 - x\\x - 4 = 0\end{array} \right. \Leftrightarrow x = 4\left( {tmdk} \right)$

Vậy phương trình có nghiệm duy nhất $x = 4$