Đề kiểm tra học kì 1 Toán 9 - Đề số 29 — Không quảng cáo

Đề bài

PHẦN TRẮC NGHIỆM (3,0 điểm )

Câu 1: Giá trị của biểu thức $\sqrt 2 + \sqrt 8$ là:

A . $4$ .

B . $5\sqrt 2$ .

C . $\sqrt {10}$ .

D . $3\sqrt 2$ .

Câu 2: Đồ thị hàm số $y = 1-2x$ đi qua điểm nào?

A . $M( - 2; - 3)$ .

B . $N( - 2;5)$ .

C . $P( - 3;2)$ .

D . $Q(2;5)$ .

Câu 3: Cho đường thẳng $d:y = ax + 2$ đi qua điểm $E\left( {1;1} \right)$ . Hệ số góc của đường thẳng $d$ là:

A. $3$

B. $1$

C. $2$

D. $- 1$

Câu 4: Đường thẳng $y = 2x + 1$ song song với đường thẳng nào sau đây?

A. $y = x + 1$ .

B. $y = 2 + x$ .

C. $y = 2x - 2022$ .

D. $y = - \frac{1}{2}x + 1$ .

Câu 5: Cho đường tròn $\left( {O;6\,cm} \right)$ , $M$ là một điểm cách điểm $O$ một khoảng $10\,cm$ . Qua $M$ kẻ tiếp tuyến với $\left( O \right)$ . Khi đó, khoảng cách từ $M$ đến tiếp điểm là:

A. $4$ $cm$ .

B . $8$ $cm$ .

C . $2\sqrt {34}$ $cm$ .

D . $18$ $cm$ .

Câu 6: Cho đường tròn $\left( {O;5\,cm} \right)$ và dây $AB$ cách tâm $O$ một khoảng bằng $3$ $cm$ . Độ dài dây$AB$ là:

A. $8$ $cm$ .

B. $6$ $cm$ .

C. $4$ $cm$ .

D. $5$ $cm$ .

PHẦN TỰ LUẬN (7,0 điểm ).

Bài 1 : (3,0 điểm)

1) Rút gọn biểu thức $P = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\frac{1}{{\sqrt x - 1}}$ với$x > 0;x \ne 1$

2) Cho hàm số $y = x + 1$ có đồ thị là đường thẳng $d$ .

a) Hàm số đã cho đồng biến hay nghịch biến trên $\mathbb{R}$ ? Tại sao?

b) Vẽ $d$ trên hệ trục tọa độ $Oxy$ .

c) Tính khoảng cách từ gốc tọa độ $O$ đến $d$ .

Bài 2 : (3,0 điểm)

Cho điểm $E$ thuộc nửa đường tròn tâm $O$ , đường kính $MN$ . Tiếp tuyến tại $N$ của nửa đường tròn tâm $O$ cắt đường thẳng $ME$ tại $D$ . Kẻ $OI$ vuông góc với $ME$ tại $I$ .

a) Chứng minh rằng tam giác $MEN$ vuông tại $E$ . Từ đó chứng minh $DE.DM = D{N^2}$ .

b) Chứng minh rẳng bốn điểm $O$ , $I$ , $D$ , $N$ cùng thuộc một đường tròn.

c) Vẽ đường tròn đường kính $OD$ , cắt nửa đường tròn tâm $O$ tại điểm thứ hai là $A$ . Chứng minh rằng $DA$ là tiếp tuyến của nửa đường tròn tâm $O$ và $\angle DEA = \angle DAM$ .

Bài 3 : (1,0 điểm)

Cho $A = \frac{{3 - \sqrt {3 + \sqrt {3 + \sqrt {3 + ... + \sqrt 3 } } } }}{{6 - \sqrt {3 + \sqrt {3 + \sqrt {3 + ... + \sqrt 3 } } } }}$ tử số có $2022$ dấu căn, mẫu số có $2021$ dấu căn.

Chứng minh $A < \frac{1}{4}$ .

----- Hết -----

Lời giải

Phần t rắc nghiệm

Câu 1: Giá trị của biểu thức $\sqrt 2 + \sqrt 8$ là:

A . $4$ .

B . $5\sqrt 2$ .

C . $\sqrt {10}$ .

D . $3\sqrt 2$ .

Phương pháp giải

Sử dụng hằng đẳng thức: $\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.$

Lời giải

$\begin{array}{l}\,\,\,\,\,\sqrt 2 + \sqrt 8 \\ = \sqrt 2 + \sqrt {2.{2^2}} \\ = \sqrt 2 + 2\sqrt 2 \\ = 3\sqrt 2 \end{array}$

Chọn D.

Câu 2: Đồ thị hàm số $y = 1-2x$ đi qua điểm nào?

A . $M( - 2; - 3)$ .

B . $N( - 2;5)$ .

C . $P( - 3;2)$ .

D . $Q(2;5)$ .

Phương pháp giải

Đồ thị hàm số $y = ax + b$ đi qua điểm $M\left( {{x_0};{y_0}} \right)$ nếu ${y_0} = a{x_0} + b$

Lời giải

+ Thay $x = - 2$ vào hàm số, ta được: $1 - 2.\left( { - 2} \right) = 5 \ne - 3 \Rightarrow$ Hàm số không đi qua điểm $M\left( { - 2; - 3} \right)$

$\Rightarrow$ Loại đáp án A

+ Thay $x = - 2$ vào hàm số, ta được: $1 - 2.\left( { - 2} \right) = 5 \Rightarrow$ Hàm số đi qua điểm $N\left( { - 2;5} \right)$

$\Rightarrow$ Chọn đáp án B

Chọn B.

Câu 3: Cho đường thẳng $d:y = ax + 2$ đi qua điểm $E\left( {1;1} \right)$ . Hệ số góc của đường thẳng $d$ là:

A. $3$

B. $1$

C. $2$

D. $- 1$

Phương pháp giải

Đồ thị hàm số $y = ax + b$ đi qua điểm $M\left( {{x_0};{y_0}} \right)$ nếu ${y_0} = a{x_0} + b$

Đường thẳng $y = ax + b$ có hệ số góc là $a$

Lời giải

Đường thẳng $d:y = ax + 2$ đi qua điểm $E\left( {1;1} \right)$ nên ta có: $a + 2 = 1 \Leftrightarrow a = - 1$

Vậy hệ số góc của đường thẳng là $a = - 1$

Chọn D.

Câu 4: Đường thẳng $y = 2x + 1$ song song với đường thẳng nào sau đây?

A. $y = x + 1$ .

B. $y = 2 + x$ .

C. $y = 2x - 2022$ .

D. $y = - \frac{1}{2}x + 1$ .

Phương pháp giải

Đường thẳng $\left( d \right):y = ax + b$ song song với đường thẳng $\left( {d'} \right):y = a'x + b'$ khi và chỉ khi $\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$ .

Lời giải

Ta có: $\left\{ \begin{array}{l}2 = 2\\1 \ne - 2022\end{array} \right.$

Do đó, đường thẳng $y = x + 1$ song song với đường thẳng $y = 2x - 2022$

Chọn C.

Câu 5: Cho đường tròn $\left( {O;6\,cm} \right)$ , $M$ là một điểm cách điểm $O$ một khoảng $10\,cm$ . Qua $M$ kẻ tiếp tuyến với $\left( O \right)$ . Khi đó, khoảng cách từ $M$ đến tiếp điểm là:

A. $4$ $cm$ .

B . $8$ $cm$ .

C . $2\sqrt {34}$ $cm$ .

D . $18$ $cm$ .

Phương pháp giải

Áp dụng định lý Py – ta – go với tam giác vuông.

Lời giải

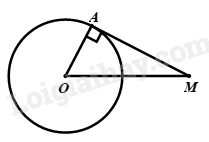
$MA$  là tiếp tuyến của đường tròn tại $A \Rightarrow OA \bot AM \Rightarrow \angle OAM = {90^0}$

$\Rightarrow \Delta AOM$ vuông tại $A$

$\Delta AOM$ vuông tại $A$ , theo định lý Py – ta – go, ta có:

$\begin{array}{l}\,\,\,\,\,\,\,\,O{M^2} = O{A^2} + A{M^2}\\ \Leftrightarrow A{M^2} = O{M^2} - O{A^2}\\ \Leftrightarrow A{M^2} = {10^2} - {6^2}\\ \Leftrightarrow A{M^2} = 64\\ \Rightarrow AM = 8\left( {cm} \right)\end{array}$

Chọn A.

Câu 6: Cho đường tròn $\left( {O;5\,cm} \right)$ và dây $AB$ cách tâm $O$ một khoảng bằng $3$ $cm$ . Độ dài dây$AB$ là:

A. $8$ $cm$ .

B. $6$ $cm$ .

C. $4$ $cm$ .

D. $5$ $cm$ .

Phương pháp giải

Xét $\left( O \right)$ : kẻ $OH \bot AB$

$\Rightarrow H$ là trung điểm của $AB \Rightarrow AH = \frac{1}{2}AB$

$\Delta AOH$ vuông tại $H \Rightarrow AH \Rightarrow AB$

Lời giải

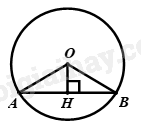
Xét $\left( O \right)$ : kẻ $OH \bot AB$

Ta có: $AB$ là dây không đi qua tâm $O$

$\Rightarrow H$ là trung điểm của $AB \Rightarrow AH = \frac{1}{2}AB$

$\Delta AHB$ vuông tại $H$ , theo định lý Py – ta – go, ta có:

$\begin{array}{l}\,\,\,\,\,\,\,\,A{O^2} = A{H^2} + O{H^2}\\ \Leftrightarrow A{H^2} = A{O^2} - O{H^2}\\ \Leftrightarrow A{H^2} = {5^2} - {3^2}\\ \Leftrightarrow A{H^2} = 16\\ \Rightarrow AH = 4\left( {cm} \right)\\ \Rightarrow AB = 2AH = 8\left( {cm} \right)\end{array}$

Chọn A.

II. TỰ LUẬN

1) Rút gọn biểu thức $P = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\frac{1}{{\sqrt x - 1}}$ với$x > 0;x \ne 1$

2) Cho hàm số $y = x + 1$ có đồ thị là đường thẳng $d$ .

a) Hàm số đã cho đồng biến hay nghịch biến trên $\mathbb{R}$ ? Tại sao?

b) Vẽ $d$ trên hệ trục tọa độ $Oxy$ .

c) Tính khoảng cách từ gốc tọa độ $O$ đến $d$ .

Phương pháp giải

1) Xác định mẫu thức chung

Thực hiện các phép toán với các phân thức đại số

2) a) Hàm số $y = ax + b$ đồng biến trên $\mathbb{R} \Leftrightarrow a > 0$

Hàm số $y = ax + b$ nghịch biến trên $\mathbb{R} \Leftrightarrow a < 0$

b) Vẽ đồ thị của hàm số $y = ax + b$

+ Lập bảng giá trị tương ứng của $x$ và $y$

+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.

c) Gọi $H$ là trung điểm của $AB$ thì $OH \bot AB$ .

$\Rightarrow OH$ là khoảng cách từ $O$ đến đường thẳng $d$

Lời giải

1)

$\begin{array}{l}P = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\frac{1}{{\sqrt x - 1}}\\P = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\frac{1}{{\sqrt x - 1}}\\P = \frac{{x - 1}}{{\sqrt x (\sqrt x - 1)}}:\frac{1}{{\sqrt x - 1}}\\P = \frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\left( {\sqrt x - 1} \right)\\P = \frac{{x - 1}}{{\sqrt x }}\end{array}$

Vậy $P = \frac{{x - 1}}{{\sqrt x }}$ với$x > 0;x \ne 1$

2) a) Do hệ số của $x$ là $1 > 0$ nên hàm số đã cho đồng biến trên $\mathbb{R}$

b) Với $x = 0$ thì $y = 1$ ; với $x = - 1$ thì $y = 0$ do đó $d$ đi qua điểm $A\left( { - 1;0} \right),B\left( {0;1} \right)$ .

Vẽ đồ thị:

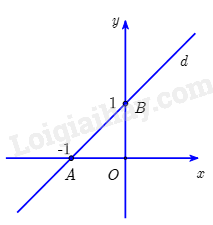
c) Do $OA = OB = 1$ nên $\Delta AOB$ vuông cân tại $O$ . Gọi $H$ là trung điểm của $AB$ thì $OH \bot AB$ .

Do đó, khoảng cách từ $O$ đến $d$ bằng $OH = \frac{1}{2}AB = \frac{1}{2}\sqrt {O{A^2} + O{B^2}} = \frac{{\sqrt 2 }}{2}$ .

Vậy khoảng các từ gốc tọa độ $O$ đến $d$ là $\frac{{\sqrt 2 }}{2}$ (đvđd).

Bài 2 : (3,0 điểm)

Cho điểm $E$ thuộc nửa đường tròn tâm $O$ , đường kính $MN$ . Tiếp tuyến tại $N$ của nửa đường tròn tâm $O$ cắt đường thẳng $ME$ tại $D$ . Kẻ $OI$ vuông góc với $ME$ tại $I$ .

a) Chứng minh rằng tam giác $MEN$ vuông tại $E$ . Từ đó chứng minh $DE.DM = D{N^2}$ .

b) Chứng minh rẳng bốn điểm $O$ , $I$ , $D$ , $N$ cùng thuộc một đường tròn.

c) Vẽ đường tròn đường kính $OD$ , cắt nửa đường tròn tâm $O$ tại điểm thứ hai là $A$ . Chứng minh rằng $DA$ là tiếp tuyến của nửa đường tròn tâm $O$ và $\angle DEA = \angle DAM$ .

Phương pháp giải

a) Sử dụng hệ thức lượng trong tam giác vuông

b) $I,N$ thuộc đường tròn đường kính $OD$

c) Dấu hiệu nhận biết tiếp tuyến của đường tròn, chứng minh $OA \bot AD$ tại $A$

$\Delta DEA\backsim \Delta DAM\left( c.g.c \right)\Rightarrow \angle DEA=\angle DAM$

Lời giải

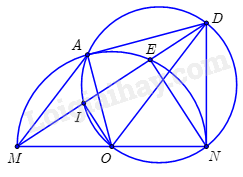
a) $\Delta MEN$ nội tiếp $\left( O \right)$ mà $MN$ là đường kính của $(O) \Rightarrow \Delta MEN$ vuông tại $E$ $\Rightarrow NE \bot MD$ .

Do $ND$ là tiếp tuyến của $\left( O \right)$ $\Rightarrow MN \bot ND$ $\Rightarrow \Delta MND$ vuông tại $N$ có $NE \bot MD$

$\Rightarrow DE.DM = D{N^2}$ (theo hệ thức lượng trong tam giác vuông) (đpcm).

b) Do $OI \bot ME$ tại $I$ nên $\Delta OID$ vuông tại $I$ $\Rightarrow I$ thuộc đường tròn đường kính $OD$ .(1)

Do $ON \bot ND$ tại$N$ nên $\Delta OND$ vuông tại $N$

$\Rightarrow N$ thuộc đường tròn đường kính $OD$ . (2)

Từ (1) và (2) suy ra $4$ điểm $O,I,D,N$ cùng thuộc đường tròn đường kính $OD$ (đpcm).

c) $\Delta OAD$ nội tiếp đường tròn đường kính $OD$ $\Rightarrow \Delta OAD$ vuông tại$A$

$\Rightarrow OA \bot DA$ mà $A$ thuộc đường tròn tâm $O$ .

$\Rightarrow DA$ là tiếp tuyến của đường tròn tâm $O$ (theo dhnb).

Do$DA;DN$ là 2 tiếp tuyến của đường tròn tâm $O$ .

$\Rightarrow DA = DN$ (tính chất 2 tiếp tuyến cắt nhau).

Mà $DE.DM = D{N^2}$

$\Rightarrow DE.DM = D{A^2} \Rightarrow \frac{{DE}}{{DA}} = \frac{{DA}}{{DM}}$

Từ đó chứng minh $\Delta DEA$ đồng dạng với $\Delta DAM$ (c.g.c)

$\Rightarrow \angle DEA = \angle DAM$ (đpcm).

Bài 3 : (1,0 điểm)

Cho $A = \frac{{3 - \sqrt {3 + \sqrt {3 + \sqrt {3 + ... + \sqrt 3 } } } }}{{6 - \sqrt {3 + \sqrt {3 + \sqrt {3 + ... + \sqrt 3 } } } }}$ tử số có $2022$ dấu căn, mẫu số có $2021$ dấu căn.

Chứng minh $A < \frac{1}{4}$ .

Phương pháp giải

Đặt $\sqrt {3 + \sqrt {3 + \sqrt {3 + ... + \sqrt 3 } } } = a$ $\left( {a > 1} \right)$ (có 2022 dấu căn)

Tính giá trị của $A$ theo $a$ , từ đó biện luận và chứng minh.

Lời giải

Đặt $\sqrt {3 + \sqrt {3 + \sqrt {3 + ... + \sqrt 3 } } } = a$ $\left( {a > 1} \right)$ (có 2022 dấu căn)

$\Leftrightarrow 3 + \sqrt {3 + \sqrt {3 + \sqrt {3 + ... + \sqrt 3 } } } = {a^2}$ (có 2021 dấu căn)

$\Leftrightarrow \sqrt {3 + \sqrt {3 + \sqrt {3 + ... + \sqrt 3 } } } = {a^2} - 3$ .

Khi đó $A = \frac{{3 - a}}{{6 - {a^2} + 3}} = \frac{1}{{a + 3}}$ .

Do $a > 1 \Rightarrow a + 3 > 4 > 0 \Leftrightarrow \frac{1}{{a + 3}} < \frac{1}{4}$ .

Vậy $A < \frac{1}{4}$ (đpcm).