Đề kiểm tra học kì 1 Toán 9 - Đề số 22
Đáp án và lời giải chi tiết Đề số 22 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Đề bài
Câu 1: (2 điểm) Tính:
a) \(\frac{{\sqrt {27} - \sqrt {15} }}{{3 - \;\sqrt 5 }} + \frac{4}{{2 + \sqrt 3 }}\;\; - \;\frac{6}{{\sqrt 3 }}\)
b) \(\frac{{\sqrt x }}{{\sqrt x + 2}} - \frac{2}{{\sqrt x - 2}} + \frac{8}{{x - 4}}(x \ge 0;x \ne 4)\)
Câu 2: ( 1,5 điểm) Cho hàm số y = x + 3 có đồ thị (d) và hàm số y = -2x có đồ thị (d’)
a) Vẽ (d) và (d’) trên một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d) và (d’) bằng phép toán.
Câu 3: ( 1 điểm) Giải phương trình: \(2\sqrt {x - 2} + \frac{1}{3}\sqrt {9x - 18} - \frac{1}{5}\sqrt {25x - 50} = 12\)
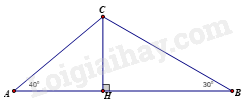
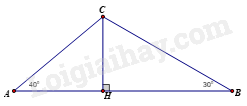
Câu 4: ( 1 điểm) Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết máy bay cách mặt đất là 180m, góc nhìn thấy máy bay tạo với mặt đất tại vị trí A là 40 0 và tại vị trí B là 30 0 . Hãy tìm khoảng cách giữa hai vị trí A và B? ( Làm tròn đến mét )
Câu 5: ( 0,75 điểm) Rừng ngập mặn Cần Giờ (còn gọi là RừngSác), được UNESCO công nhận là khu dự trữ sinh quyển của thế giới đầu tiên ở Việt Nam vào ngày 21/01/2000. Diện tích rừng phủ xanh được cho bởi hàm số S = 0,05t + 3,14 trong đó S tính bằng nghìn héc-ta, t tính bằng số năm kể từ năm 2000.
a) Tính diện tích Rừng Sác được phủ xanh vào năm 2000, 2022?
b) Hãy cho biết diện tích rừng Sác được phủ xanh đạt 3,64 nghìn hecta vào năm nào?
Câu 6: (0,75điểm) Vào ngày “ Black Friday” cửa hàng điện tử giám giá 10% cho các mặt hàng. Nếu mua online thì được giảm tiếp 5% trên giá đã giảm.
a) Bình mua online 1 bộ máy vi tính với giá niêm yết là 15 000 000 đồng (đã bao gồm thuế VAT) vào ngày trên thì phải trả bao nhiêu tiền?
b) Cùng lúc đó, Bình mua thêm đĩa cài đặt phần mềm diệt virus ABC bản quyền 1 năm và phải trả tất cả là 13 081 500 đồng. Hỏi đĩa cài đặt phần mềm diệt virus ABC giá niêm yết là bao nhiêu? (Kết quả làm tròn đến chữ số hàng nghìn
Câu 7: ( 3 điểm) Cho điểm M nằm ngoài đường tròn (O), từ M vẽ 2 tiếp tuyến MA; MB đến đường tròn (A; B là các tiếp điểm), vẽ đường kính AE, OM cắt AB tại H.
a) Chứng minh: OM \( \bot \) AB
b) ME cắt đường tròn (O) tại D. Chứng minh: MD.ME = MH.MO
c) Gọi F là trung điểm của DE. OF cắt AB tại K. Chứng minh: KD là tiếp tuyến của đường tròn (O)
Lời giải
Câu 1: (2 điểm) Tính:
a) \(\frac{{\sqrt {27} - \sqrt {15} }}{{3 - \;\sqrt 5 }} + \frac{4}{{2 + \sqrt 3 }}\;\; - \;\frac{6}{{\sqrt 3 }}\)
b) \(\frac{{\sqrt x }}{{\sqrt x + 2}} - \frac{2}{{\sqrt x - 2}} + \frac{8}{{x - 4}}(x \ge 0;x \ne 4)\)
Phương pháp
Sử dụng công thức khai phương căn bậc hai, trục căn thức.
Lời giải
a) \(\frac{{\sqrt {27} - \sqrt {15} }}{{3 - \;\sqrt 5 }} + \frac{4}{{2 + \sqrt 3 }}\;\; - \;\frac{6}{{\sqrt 3 }}\)
= \(\frac{{\sqrt 3 \left( {3 - \;\sqrt 5 } \right)}}{{3 - \sqrt 5 }}\) + \(\frac{{4\left( {\;2 - \;\sqrt 3 } \right)}}{{\left( {2 + \;\sqrt 3 } \right)\left( {\;2 - \;\sqrt 3 } \right)}}\)- 2\(\sqrt 3 \)
= \(\sqrt 3 \) + \(\frac{{4\left( {\;2 - \;\sqrt 3 } \right)}}{1}\) - 2\(\sqrt 3 \)
= \(\sqrt 3 + 8 - \;4\sqrt 3 \) - 2\(\sqrt 3 \)
= 8 - 5\(\sqrt 3 \)
b) \(\frac{{\sqrt x }}{{\sqrt x + 2}} - \frac{2}{{\sqrt x - 2}} + \frac{8}{{x - 4}}(x \ge 0;x \ne 4)\)
\( = \frac{{\sqrt x \left( {\sqrt x - 2} \right) - 2\left( {\sqrt x + 2} \right) + 8}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\( = \frac{{x - 2\sqrt x - 2\sqrt x - 4 + 8}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\( = \frac{{x - 4\sqrt x + 4}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\( = \frac{{{{\left( {\sqrt x - 2} \right)}^2}}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\)
\( = \frac{{\sqrt x - 2}}{{\sqrt x + 2}}\)
Câu 2: ( 1,5 điểm) Cho hàm số y = x + 3 có đồ thị (d) và hàm số y = -2x có đồ thị (d’)
a) Vẽ (d) và (d’) trên một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d) và (d’) bằng phép toán.
Phương pháp
a) Lấy hai điểm thuộc đồ thị hàm số, ta được đồ thị của hàm số đó.
b) Viết phương trình hoành độ giao điểm của (d) và (d’). Tìm nghiệm của phương trình. Thay giá trị x tìm được để tìm y.
Lời giải
a) Ta thấy:
+) \(A\left( {0;3} \right),B\left( { - 3;0} \right)\) thuộc đồ thị hàm số y = x + 3.
+) \(O\left( {0;0} \right),C\left( {1; - 2} \right)\) thuộc đồ thị hàm số y = -2x.
Từ đó ta có đồ thị của hai hàm số:
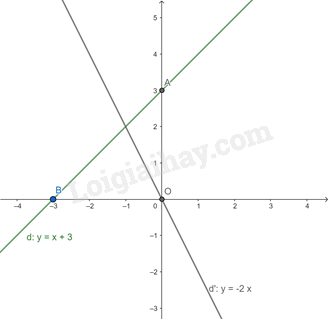
b) Ta có phương trình hoành độ giao điểm của hai đường thẳng (d) và (d’) là:
\(\begin{array}{l}x + 3 = - 2x\\ \Leftrightarrow x + 2x = - 3\\ \Leftrightarrow 3x = - 3\\ \Leftrightarrow x = - 1\end{array}\)
Với x = - 1 ta có \(y = - 2.\left( { - 1} \right) = 2\) ta được điểm G(-1; 2)
Vậy giao điểm của (d) và (d’) là điểm G(-1; 2).
Câu 3: ( 1 điểm) Giải phương trình: \(2\sqrt {x - 2} + \frac{1}{3}\sqrt {9x - 18} - \frac{1}{5}\sqrt {25x - 50} = 12\)
Phương pháp
Sử dụng công thức khai phương căn bậc hai để có nhân tử chung.
Lời giải
\(2\sqrt {x - 2} + \frac{1}{3}\sqrt {9x - 18} - \frac{1}{5}\sqrt {25x - 50} = 12\) (ĐK: \(x \ge 2\))
\( \Leftrightarrow \)\(2\sqrt {x - 2} + \frac{1}{3}\sqrt {9\left( {x - 2} \right)} - \frac{1}{5}\sqrt {25\left( {x - 2} \right)} = 12\)
\( \Leftrightarrow \)\(2\sqrt {x - 2} + \sqrt {\left( {x - 2} \right)} - \sqrt {\left( {x - 2} \right)} = 12\)
\( \Leftrightarrow \)\(2\sqrt {x - 2} = 12\)
\( \Leftrightarrow \)\(\sqrt {x - 2} = 6\) ( Điều kiện: 6\( \ge 0\), luôn đúng)
x – 2 = 36
\( \Leftrightarrow \)x = 38 (TM)
Vậy nghiệm của phương trình là x = 38 .
Câu 4: ( 1 điểm) Điểm hạ cánh của một máy bay trực thăng ở giữa hai người quan sát A và B. Biết máy bay cách mặt đất là 180m, góc nhìn thấy máy bay tạo với mặt đất tại vị trí A là 40 0 và tại vị trí B là 30 0 . Hãy tìm khoảng cách giữa hai vị trí A và B? ( Làm tròn đến mét )
Phương pháp
Sử dụng tỉ số lượng giác của góc nhọn.
Lời giải
Xét tam giác AHC vuông tại H có \(\widehat A = {40^0}\) nên \(\cot \left( {{{40}^0}} \right) = \frac{{AH}}{{HC}} \Rightarrow AH = HC.\cot \left( {{{40}^0}} \right) = 180.\cot \left( {{{40}^0}} \right) \approx 215\left( m \right)\)
Xét tam giác BHC vuông tại H có \(\widehat B = {30^0}\) nên \(\cot \left( {{{30}^0}} \right) = \frac{{BH}}{{CH}} \Rightarrow BH = CH.\cot \left( {{{30}^0}} \right) = 180.\cot \left( {{{30}^0}} \right) \approx 312\left( m \right)\)
Vậy khoảng cách giữa hai vị trí A và B là: AB = AH + BH = 215 + 312 = 527(m).
Câu 5: ( 0,75 điểm) Rừng ngập mặn Cần Giờ (còn gọi là RừngSác), được UNESCO công nhận là khu dự trữ sinh quyển của thế giới đầu tiên ở Việt Nam vào ngày 21/01/2000. Diện tích rừng phủ xanh được cho bởi hàm số S = 0,05t + 3,14 trong đó S tính bằng nghìn héc-ta, t tính bằng số năm kể từ năm 2000.
a) Tính diện tích Rừng Sác được phủ xanh vào năm 2000, 2022?
b) Hãy cho biết diện tích rừng Sác được phủ xanh đạt 3,64 nghìn hecta vào năm nào?
Phương pháp
a) Thay t = 2000 – 2000 và t = 2022 - 2000 vào hàm số để tính diện tích Rừng Sác vào năm 2000 và 2022.
b) Thay S = 3,64 vào hàm số để tính số năm để Rừng Sác được phủ xanh. Lấy kết quả cộng 2000 để tính được năm.
Lời giải
a) Diện tích Rừng Sác vào năm 2000:
S = 0,05(2000 – 2000) + 3,14 = 3,14 (nghìn héc-ta)
Diện tích Rừng Sác vào năm 2022:
S = 0,05(2022 – 2000) + 3,14 = 4,24 (nghìn héc-ta)
b) Thay S = 3,64
Ta được: 0,05.t + 3,14 = 3,64 suy ra t = 10.
Vậy Rừng Sác được phủ xanh đạt 3,64 nghìn hecta vào năm 2000 + 10 = 2010
Câu 6: (0,75điểm) Vào ngày “ Black Friday” cửa hàng điện tử giám giá 10% cho các mặt hàng. Nếu mua online thì được giảm tiếp 5% trên giá đã giảm.
a) Bình mua online 1 bộ máy vi tính với giá niêm yết là 15 000 000 đồng (đã bao gồm thuế VAT) vào ngày trên thì phải trả bao nhiêu tiền?
b) Cùng lúc đó, Bình mua thêm đĩa cài đặt phần mềm diệt virus ABC bản quyền 1 năm và phải trả tất cả là 13 081 500 đồng. Hỏi đĩa cài đặt phần mềm diệt virus ABC giá niêm yết là bao nhiêu? (Kết quả làm tròn đến chữ số hàng nghìn
Phương pháp
Viết phương trình biểu diễn số tiền Bình phải trả và tính.
Lời giải
a) Số tiền Bình phải trả khi mua 1 bộ máy vi tính:
15 000 000.(1 – 10%)(1 – 5%) = 12 825 000 (đồng)
b) Số tiền Bình mua đĩa cài đặt phần mềm diệt virus ABC:
13 081 500 – 12 825 000 = 256 500 (đồng)
Giá niêm yết của đĩa cài đặt phần mềm diệt virus ABC:
256 500 : (1 – 5%) : (1 – 10%) = 300 000 (đồng)
Câu 7: ( 3 điểm) Cho điểm M nằm ngoài đường tròn (O), từ M vẽ 2 tiếp tuyến MA; MB đến đường tròn (A; B là các tiếp điểm), vẽ đường kính AE, OM cắt AB tại H.
a) Chứng minh: OM \( \bot \) AB
b) ME cắt đường tròn (O) tại D. Chứng minh: MD.ME = MH.MO
c) Gọi F là trung điểm của DE. OF cắt AB tại K. Chứng minh: KD là tiếp tuyến của đường tròn (O)
Phương pháp
a) Sử dụng tính chất của hai tiếp tuyến cắt nhau.
b) Chứng minh AM 2 = MD.ME, AM 2 = MH.MO suy ra MD.ME = MH.MO
c) Chứng minh:
OF.OK = OD 2
ΔOFD đồng dạng ΔODK (c-g-c)
KD là tiếp tuyến của đường tròn (O)
Lời giải
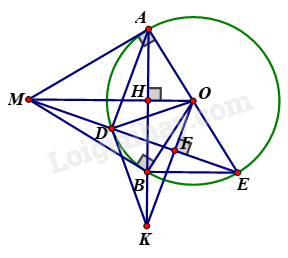
a) Ta có : OA = OB ( = R ) và MA = MB ( tính chất 2 tiếp tuyến cắt nhau)
=> OM là đường trung trực của AB
=> OM \( \bot \) AB tại H
b) Xét tam giác MAE vuông tại A có AD là đường cao nên AM 2 = MD.ME. (1)
Xét tam giác MAO vuông tại A có AH là đường cao nên AM 2 = MH.MO. (2)
Từ (1) và (2) suy ra MD.ME = MH.MO.
c) Ta có O là trung điểm của AE, F là trung điểm của DE => OF là đường trung bình của tam giác ADE => OF // AD. Mà AD \( \bot \) DE => OF \( \bot \) DE
Xét \(\Delta OHK\) và \(\Delta OFM\), ta có:
\(\widehat {MOK}\) chung
\(\widehat {OHK} = \widehat {OFM} = {90^0}\)
Nên $\Delta O H K \backsim \Delta O F M(g . g)$
Do đó \(\frac{{OH}}{{OF}} = \frac{{OK}}{{OM}} \Rightarrow OH.OM = OF.OK\)
Xét \(\Delta MAO\) vuông tại \(A\) có AH là đường cao
Nên \(O{A^2} = OH.OM\) (hệ thức lượng)
Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{OH.OM = OF.OK({\rm{cmt}})}\\{O{A^2} = OH.OM({\rm{cmt}})}\\{OA = OD = R}\end{array}} \right.\)
Nên \(O{D^2} = OF.OK \Rightarrow \frac{{OD}}{{OF}} = \frac{{OK}}{{OD}}\)
Xét \(\Delta ODK\) và \(\Delta OFD\), ta có:
\(\widehat {DOK}\) là góc chung
\(\frac{{OD}}{{OF}} = \frac{{OK}}{{OD}}({\rm{cmt}})\)
Nên $\Delta O D K \backsim \Delta O F D$ (c.g.c)
Do đó \(\widehat {ODK} = \widehat {OFD} = {90^0}\)
\( \Rightarrow OD \bot DK\)
Vậy KD là tiếp tuyến của \((O)\).