Đề thi giữa học kì 1 Vật lí 11 Chân trời sáng tạo - Đề số 7
Đề thi giữa học kì 1 - Đề số 7
Đề bài
Một vật dao động điều hòa theo phương trình x = 6cos(4πt) cm. Tần số dao động của vật là
-
A.
f = 6 Hz.
-
B.
f = 4 Hz.
-
C.
f = 2 Hz.
-
D.
f = 0,5 Hz.
Một vật nhỏ dao động với phương trình \(x = 6\cos \omega t(cm)\). Dao động của vật nhỏ có biên độ là
-
A.
2 cm.
-
B.
6 cm.
-
C.
3 cm.
-
D.
12 cm.
Biểu thức li độ của vật dao động điều hòa có dạng x = Acos(ωt + φ) cm, vận tốc của vật có giá trị cực đại là
-
A.
\({v_{\max }} = 2A\omega \)
-
B.
\({v_{\max }} = {A^2}\omega \)
-
C.
\({v_{\max }} = A{\omega ^2}\)
-
D.
\({v_{\max }} = A\omega \)
Một vật nhỏ dao động điều hòa với tần số 5Hz, biết tốc độ của vật khi qua vị trí cân bằng là \(30\pi {\rm{ }}\left( {cm/s} \right)\). Biên độ dao động của vật là
-
A.
\(A = 2cm\)
-
B.
\(A = 4cm\)
-
C.
\(A = 6cm\)
-
D.
\(A = 3cm\)
Một chất điểm dao động điều hoà với phương trình dạng \(x = 5\cos \left( {\pi t + \frac{\pi }{6}} \right)cm.\). Lấy π 2 = 10, biểu thức gia tốc tức thời của chất điểm là
-
A.
\(a = 50\cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
B.
\(a = - 50\sin \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
C.
\(a = - 50\cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
D.
\(a = 5\pi \cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
Một vật dao động điều hòa trên quỹ đạo thẳng nằm ngang dài 20 cm. Biết trong khoảng thời gian 10 s, vật thực hiện được 20 dao động toàn phần. Gia tốc của vật có giá trị cực đại bằng
-
A.
\(160\pi {\rm{ }}cm/{s^2}\)
-
B.
\(160{\pi ^2}{\rm{ }}cm/{s^2}\)
-
C.
\(40{\pi ^2}{\rm{ }}cm/{s^2}\)
-
D.
\(40\pi {\rm{ }}cm/{s^2}\)
Trong dao động điều hoà, gia tốc biến đổi
-
A.
cùng pha với vận tốc.
-
B.
ngược pha với vận tốc.
-
C.
sớm pha 0,5π so với vận tốc.
-
D.
trễ pha 0,5π so với vận tốc.
Một vật dao động điều hòa có phương trình \(x = A\cos \left( {\omega t + \varphi } \right)\). Gọi v là vận tốc của vật. Hệ thức đúng là
-
A.
\(\frac{{{x^2}}}{{{\omega ^2}}} + \frac{{{v^2}}}{{{\omega ^4}}} = {A^2}.\)
-
B.
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}.\)
-
C.
\(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^4}}} = {A^2}.\)
-
D.
\(\frac{{{\omega ^2}}}{{{v^2}}} + \frac{{{x^2}}}{{{\omega ^2}}} = {A^2}.\)
Đồ thị biểu diễn gia tốc a của một dao động điều hòa theo thời gian có dạng như hình bên. Pha ban đầu của dao động là
-
A.
φ = 0.
-
B.
φ = π (rad).
-
C.
φ = π/2 (rad).
-
D.
φ = –π/2 (rad).
Một con lắc đơn, quả nặng có khối lượng 40 g dao động nhỏ với chu kỳ 2 s. Nếu gắn thêm một gia trọng có khối lượng 120 g thì con lắc sẽ dao động nhỏ với chu kỳ:
-
A.
8 s
-
B.
4 s
-
C.
2 s
-
D.
0,25 s
Một con lắc lò xo nằm ngang có chiều dài tự nhiên là 30 cm. Đưa vật tới vị trí lò xo bị nén 5 cm rồi thả nhẹ cho vật dao động điều hòa. Trong quá trình dao động, chiều dài lớn nhất của lò xo là
-
A.
25 cm.
-
B.
30 cm.
-
C.
35 cm.
-
D.
40 cm.
Con lắc lò xo có k = 100N/m, dao động với A = 4cm. Khi vật có li độ 1cm thì động năng của vật:
-
A.
0,08J.
-
B.
0,04J.
-
C.
0,075J.
-
D.
0,02J.
Con lắc lò xo dao động điều hòa theo phương ngang với biên độ\(A\) . Li độ vật khi động năng bằng một nửa thế năng của lò xo là
-
A.
\(x = \pm A\sqrt 3 \).
-
B.
\(x = \pm A\sqrt {\frac{2}{3}} \).
-
C.
\(x = \pm \frac{A}{2}\).
-
D.
\(x = \pm \frac{{A\sqrt 3 }}{2}\).
Một con lắc lò xo dao động điều hoà với biên độ 4 cm. Xác định li độ của vật để động năng của vật và thế năng đàn hồi của lò xo có giá trị bằng nhau:
-
A.
x = ± 2 cm.
-
B.
x = ± \(\sqrt 2 \) cm.
-
C.
x = ± \(2\sqrt 2 \) cm.
-
D.
x = ±4 cm.
Cơ năng đàn hồi của hệ vật và lò xo
-
A.
bằng động năng của vật.
-
B.
bằng tổng động năng của vật và thế năng đàn hồi của lò xo.
-
C.
bằng thế năng đàn hồi của lò xo.
-
D.
bằng động năng của vật và cũng bằng thế năng đàn hồi của lò xo.
Hiện tượng cộng hưởng chỉ xảy ra với
-
A.
dao động riêng.
-
B.
dao động điều hòa.
-
C.
dao động tắt dần.
-
D.
dao động cưỡng bức.
Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là:
-
A.
biên độ và tốc độ.
-
B.
biên độ và gia tốc.
-
C.
biên độ và năng lượng.
-
D.
li độ và tốc độ.
Một chất điểm dao động điều hòa dọc theo trục Ox với phương trình x = 0,5cos(2πt) (dm). Quãng đường đi được của chất điểm trong 5 chu kì dao động (tính theo đơn vị cm) là:
-
A.
100 cm.
-
B.
10 cm.
-
C.
20 cm.
-
D.
5 cm
a) Biên độ dao động của vật là 10 cm.
b) Pha ban đầu của vật là \( - \pi \left( {rad} \right)\)
c) Chu kì dao động của vật là 1(s)
d) Tốc độ của vật tại thời điểm 1,5s là \(10\pi \left( {cm/s} \right)\).
Một vật dao động điều hòa dọc theo trục Ox, quanh điểm gốc O, với biên độ A = 10 cm và chu kì T = 2s. Tại thời điểm t = 0, vật có li độ \(x = 10\)cm. Lấy \({\pi ^2} = 10\).
a) Phương trình dao động của vật là \(x = 10\cos \left( {\pi t} \right)\,cm\)
b) Gia tốc cực đại của vật có độ lớn là \(100\left( {cm/{s^2}} \right)\).
c) Vận tốc của vật tại vị trí có li độ \(x = 5\sqrt 3 \left( {cm} \right)\)là 50 (cm/s)
d) Thời điểm đầu tiên kể từ lúc bắt đầu dao động vật đi qua vị trí có li độ \(x = 5\left( {cm} \right)\)là 3s
a) Vận tốc cực đại của vật có độ lớn \(20\pi \left( {cm/s} \right)\).
b) Tần số của dao động là 1 (Hz).
c) Quãng đường vật đi được sau 10s là 400 m.
d) Sau 5s vật đi qua vị trí có li độ \(x = 5\left( {cm} \right)\)là 10 lần.
Cho con lắc lò xo dao động trên mặt phẳng nằm ngang không ma sát như trong hình. Con lắc lò xo thực hiện mỗi dao động mất 2,4 s. Tại t = 0, vật bắt đầu dao động từ chỗ cách vị trí cân bằng x = 3 cm.
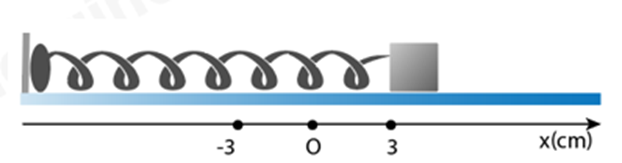
a) Chu kì dao động của con lắc là 24s.
b) Tại thời điểm \(t = 0,6s\)vật đang ở VTCB.
c) Tại \(x = 1,5\left( {cm} \right)\)vật có động năng bằng 3 lần thế năng.
d) Thời gian kể từ lúc bắt đầu dao động đến lúc vật đi qua vị trí có li độ \(x = 1,5\sqrt 2 \left( {cm} \right)\)lần thứ 2015 là 2417,1s.
Lời giải và đáp án
Một vật dao động điều hòa theo phương trình x = 6cos(4πt) cm. Tần số dao động của vật là
-
A.
f = 6 Hz.
-
B.
f = 4 Hz.
-
C.
f = 2 Hz.
-
D.
f = 0,5 Hz.
Đáp án : C
Vận dụng kiến thức về công thức tính tần số từ phương trình dao động
\(\omega = 4\pi \Rightarrow f = \frac{\omega }{{2\pi }} = \frac{{4\pi }}{{2\pi }} = 2Hz\)
Đáp án: C
Một vật nhỏ dao động với phương trình \(x = 6\cos \omega t(cm)\). Dao động của vật nhỏ có biên độ là
-
A.
2 cm.
-
B.
6 cm.
-
C.
3 cm.
-
D.
12 cm.
Đáp án : B
Vận dụng kiến thức về Xác định biên độ từ phương trình dao động điều hòa
Biên độ A = 6 cm
Đáp án: B
Biểu thức li độ của vật dao động điều hòa có dạng x = Acos(ωt + φ) cm, vận tốc của vật có giá trị cực đại là
-
A.
\({v_{\max }} = 2A\omega \)
-
B.
\({v_{\max }} = {A^2}\omega \)
-
C.
\({v_{\max }} = A{\omega ^2}\)
-
D.
\({v_{\max }} = A\omega \)
Đáp án : D
Vận dụng kiến thức về Vận tốc cực đại của dao động điều hòa
Vận tốc cực đại của dao động điều hòa được tính bằng \({v_{\max }} = A\omega \)
Đáp án: D
Một vật nhỏ dao động điều hòa với tần số 5Hz, biết tốc độ của vật khi qua vị trí cân bằng là \(30\pi {\rm{ }}\left( {cm/s} \right)\). Biên độ dao động của vật là
-
A.
\(A = 2cm\)
-
B.
\(A = 4cm\)
-
C.
\(A = 6cm\)
-
D.
\(A = 3cm\)
Đáp án : D
Vận dụng kiến thức về công thức liên hệ giữa vận tốc cực đại, biên độ và tần số góc
Biên độ dao động của vật là \({v_{{\rm{max}}}} = A.2\pi f \Rightarrow A = \frac{{{v_{{\rm{max}}}}}}{{2\pi f}} = \frac{{30\pi }}{{2\pi .5}} = 3cm\)
Đáp án: D
Một chất điểm dao động điều hoà với phương trình dạng \(x = 5\cos \left( {\pi t + \frac{\pi }{6}} \right)cm.\). Lấy π 2 = 10, biểu thức gia tốc tức thời của chất điểm là
-
A.
\(a = 50\cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
B.
\(a = - 50\sin \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
C.
\(a = - 50\cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
-
D.
\(a = 5\pi \cos \left( {\pi t + \frac{\pi }{6}} \right)cm/{s^2}\)
Đáp án : C
Vận dụng kiến thức về Gia tốc trong dao động điều hòa được tính bằng a = -ω 2 x
\(a = - {\omega ^2}x = - 50\cos \left( {\pi t + \frac{\pi }{6}} \right)cm.\)
Đáp án: C
Một vật dao động điều hòa trên quỹ đạo thẳng nằm ngang dài 20 cm. Biết trong khoảng thời gian 10 s, vật thực hiện được 20 dao động toàn phần. Gia tốc của vật có giá trị cực đại bằng
-
A.
\(160\pi {\rm{ }}cm/{s^2}\)
-
B.
\(160{\pi ^2}{\rm{ }}cm/{s^2}\)
-
C.
\(40{\pi ^2}{\rm{ }}cm/{s^2}\)
-
D.
\(40\pi {\rm{ }}cm/{s^2}\)
Đáp án : B
Vận dụng kiến thức về Gia tốc cực đại của dao động điều hòa
Tần số dao động \(f = \frac{{20}}{{10}} = 2Hz\), nên chu kỳ T = 0,5 s.
\(\begin{array}{l}\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,5}} = 4\pi rad/s\\A = \frac{{20}}{2} = 10cm\\{a_{{\rm{max}}}} = A{\omega ^2} = 10.16{\pi ^2} = 160{\pi ^2}cm/{s^2}\end{array}\)
Đáp án: B
Trong dao động điều hoà, gia tốc biến đổi
-
A.
cùng pha với vận tốc.
-
B.
ngược pha với vận tốc.
-
C.
sớm pha 0,5π so với vận tốc.
-
D.
trễ pha 0,5π so với vận tốc.
Đáp án : B
Vận dụng kiến thức về pha của gia tốc và vận tốc trong dao động điều hòa
Gia tốc ngược pha với vận tốc, vì chúng có dấu đối nhau
Đáp án: B
Một vật dao động điều hòa có phương trình \(x = A\cos \left( {\omega t + \varphi } \right)\). Gọi v là vận tốc của vật. Hệ thức đúng là
-
A.
\(\frac{{{x^2}}}{{{\omega ^2}}} + \frac{{{v^2}}}{{{\omega ^4}}} = {A^2}.\)
-
B.
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}.\)
-
C.
\(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^4}}} = {A^2}.\)
-
D.
\(\frac{{{\omega ^2}}}{{{v^2}}} + \frac{{{x^2}}}{{{\omega ^2}}} = {A^2}.\)
Đáp án : B
Vận dụng kiến thức về công thức liên hệ giữa vận tốc và li độ
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}.\)
Đáp án: B
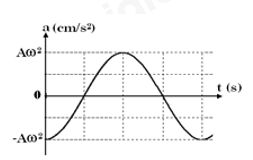
Đồ thị biểu diễn gia tốc a của một dao động điều hòa theo thời gian có dạng như hình bên. Pha ban đầu của dao động là

-
A.
φ = 0.
-
B.
φ = π (rad).
-
C.
φ = π/2 (rad).
-
D.
φ = –π/2 (rad).
Đáp án : A
Vận dụng kiến thức về đọc đồ thị
Pha ban đầu của dao động là φ = 0.
Đáp án: A
Một con lắc đơn, quả nặng có khối lượng 40 g dao động nhỏ với chu kỳ 2 s. Nếu gắn thêm một gia trọng có khối lượng 120 g thì con lắc sẽ dao động nhỏ với chu kỳ:
-
A.
8 s
-
B.
4 s
-
C.
2 s
-
D.
0,25 s
Đáp án : C
Vận dụng kiến thức về Chu kỳ dao động của con lắc đơn không phụ thuộc vào khối lượng, chỉ phụ thuộc vào chiều dài và gia tốc trọng trường
Dù có thêm vật nặng, chu kỳ vẫn là 2 s
Đáp án: C
Một con lắc lò xo nằm ngang có chiều dài tự nhiên là 30 cm. Đưa vật tới vị trí lò xo bị nén 5 cm rồi thả nhẹ cho vật dao động điều hòa. Trong quá trình dao động, chiều dài lớn nhất của lò xo là
-
A.
25 cm.
-
B.
30 cm.
-
C.
35 cm.
-
D.
40 cm.
Đáp án : C
Vận dụng kiến thức về Chiều dài lớn nhất của lò xo khi vật đạt biên độ lớn nhất.
Biên độ nén là 5 cm, nên khi dao động, chiều dài lớn nhất của lò xo là 30 + 5 = 35 cm.
Đáp án: C
Con lắc lò xo có k = 100N/m, dao động với A = 4cm. Khi vật có li độ 1cm thì động năng của vật:
-
A.
0,08J.
-
B.
0,04J.
-
C.
0,075J.
-
D.
0,02J.
Đáp án : C
Vận dụng kiến thức về Động năng
\({W_d} = \frac{1}{2}k({A^2} - {x^2}) = \frac{1}{2}.100.(0,{04^2} - 0,{01^2}) = \frac{1}{2}.100.(0,0016 - 0,0001) = 0,075\,{\rm{J}}\)
Đáp án: C
Con lắc lò xo dao động điều hòa theo phương ngang với biên độ\(A\) . Li độ vật khi động năng bằng một nửa thế năng của lò xo là
-
A.
\(x = \pm A\sqrt 3 \).
-
B.
\(x = \pm A\sqrt {\frac{2}{3}} \).
-
C.
\(x = \pm \frac{A}{2}\).
-
D.
\(x = \pm \frac{{A\sqrt 3 }}{2}\).
Đáp án : B
Vận dụng kiến thức về cơ năng
Li độ khi động năng bằng một nửa thế năng là \(x = \pm A\sqrt {\frac{2}{3}} \)
Đáp án: B
Một con lắc lò xo dao động điều hoà với biên độ 4 cm. Xác định li độ của vật để động năng của vật và thế năng đàn hồi của lò xo có giá trị bằng nhau:
-
A.
x = ± 2 cm.
-
B.
x = ± \(\sqrt 2 \) cm.
-
C.
x = ± \(2\sqrt 2 \) cm.
-
D.
x = ±4 cm.
Đáp án : C
Vận dụng kiến thức về động năng của vật và thế năng đàn hồi của lò xo
Khi W d = W t thì x = ± \(2\sqrt 2 \) cm
Đáp án: C
Cơ năng đàn hồi của hệ vật và lò xo
-
A.
bằng động năng của vật.
-
B.
bằng tổng động năng của vật và thế năng đàn hồi của lò xo.
-
C.
bằng thế năng đàn hồi của lò xo.
-
D.
bằng động năng của vật và cũng bằng thế năng đàn hồi của lò xo.
Đáp án : B
Vận dụng kiến thức về Cơ năng đàn hồi của hệ vật và lò xo
Cơ năng đàn hồi của hệ vật và lò xo bằng tổng động năng của vật và thế năng đàn hồi của lò xo
Đáp án: B
Hiện tượng cộng hưởng chỉ xảy ra với
-
A.
dao động riêng.
-
B.
dao động điều hòa.
-
C.
dao động tắt dần.
-
D.
dao động cưỡng bức.
Đáp án : D
Vận dụng kiến thức về Hiện tượng cộng hưởng
Hiện tượng cộng hưởng chỉ xảy ra với dao động cưỡng bức
Đáp án: D
Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là:
-
A.
biên độ và tốc độ.
-
B.
biên độ và gia tốc.
-
C.
biên độ và năng lượng.
-
D.
li độ và tốc độ.
Đáp án : C
Vận dụng kiến thức về dao động tắt dần
Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là biên độ và năng lượng
Đáp án: C
Một chất điểm dao động điều hòa dọc theo trục Ox với phương trình x = 0,5cos(2πt) (dm). Quãng đường đi được của chất điểm trong 5 chu kì dao động (tính theo đơn vị cm) là:
-
A.
100 cm.
-
B.
10 cm.
-
C.
20 cm.
-
D.
5 cm
Đáp án : A
Vận dụng kiến thức về quãng đường đi trong một chu kỳ là 4A
Quãng đường trong 5 chu kỳ: S = 5.4A = 5.4.5 = 100 cm
Đáp án: A
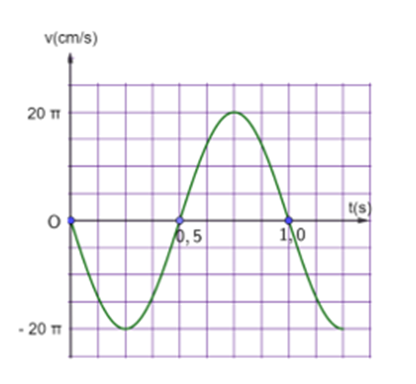
a) Biên độ dao động của vật là 10 cm.
b) Pha ban đầu của vật là \( - \pi \left( {rad} \right)\)
c) Chu kì dao động của vật là 1(s)
d) Tốc độ của vật tại thời điểm 1,5s là \(10\pi \left( {cm/s} \right)\).
a) Biên độ dao động của vật là 10 cm.
b) Pha ban đầu của vật là \( - \pi \left( {rad} \right)\)
c) Chu kì dao động của vật là 1(s)
d) Tốc độ của vật tại thời điểm 1,5s là \(10\pi \left( {cm/s} \right)\).
Vận dụng kiến thức về đọc đồ thị
a) Biên độ dao động của vật là 10 cm. Đúng
b) Pha ban đầu của vật là \( - \pi \left( {rad} \right)\). Đúng
c) Chu kì dao động của vật là 1(s). Sai
d) Tốc độ của vật tại thời điểm 1,5s là \(10\pi \left( {cm/s} \right)\). Đúng
Một vật dao động điều hòa dọc theo trục Ox, quanh điểm gốc O, với biên độ A = 10 cm và chu kì T = 2s. Tại thời điểm t = 0, vật có li độ \(x = 10\)cm. Lấy \({\pi ^2} = 10\).
a) Phương trình dao động của vật là \(x = 10\cos \left( {\pi t} \right)\,cm\)
b) Gia tốc cực đại của vật có độ lớn là \(100\left( {cm/{s^2}} \right)\).
c) Vận tốc của vật tại vị trí có li độ \(x = 5\sqrt 3 \left( {cm} \right)\)là 50 (cm/s)
d) Thời điểm đầu tiên kể từ lúc bắt đầu dao động vật đi qua vị trí có li độ \(x = 5\left( {cm} \right)\)là 3s
a) Phương trình dao động của vật là \(x = 10\cos \left( {\pi t} \right)\,cm\)
b) Gia tốc cực đại của vật có độ lớn là \(100\left( {cm/{s^2}} \right)\).
c) Vận tốc của vật tại vị trí có li độ \(x = 5\sqrt 3 \left( {cm} \right)\)là 50 (cm/s)
d) Thời điểm đầu tiên kể từ lúc bắt đầu dao động vật đi qua vị trí có li độ \(x = 5\left( {cm} \right)\)là 3s
Vận dụng kiến thức về phương trình dao động
a) \(\omega = \frac{{2\pi }}{T} = \pi ,\varphi = 0\). Phương trình dao động của vật là \(x = 10\cos \left( {\pi t} \right)\,cm\). Đúng
b) \({a_{{\rm{max}}}} = 10.{\pi ^2} = 10.10 = 100\,{\rm{cm/}}{{\rm{s}}^2}\). Đúng
c) \(v = \pm \omega \sqrt {{A^2} - {x^2}} = \pi \sqrt {{{10}^2} - {{(5\sqrt 3 )}^2}} = \pi \sqrt {100 - 75} = \pi \sqrt {25} = \pi .5 = 5\pi \) . Đúng
d) \(\cos (\pi t) = \frac{x}{A} = \frac{5}{{10}} = 0,5 \Rightarrow t = \frac{1}{3}s\). Sai
a) Vận tốc cực đại của vật có độ lớn \(20\pi \left( {cm/s} \right)\).
b) Tần số của dao động là 1 (Hz).
c) Quãng đường vật đi được sau 10s là 400 m.
d) Sau 5s vật đi qua vị trí có li độ \(x = 5\left( {cm} \right)\)là 10 lần.
a) Vận tốc cực đại của vật có độ lớn \(20\pi \left( {cm/s} \right)\).
b) Tần số của dao động là 1 (Hz).
c) Quãng đường vật đi được sau 10s là 400 m.
d) Sau 5s vật đi qua vị trí có li độ \(x = 5\left( {cm} \right)\)là 10 lần.
Vận dụng kiến thức về đọc đồ thị
a) Vận tốc cực đại của vật có độ lớn \(20\pi \left( {cm/s} \right)\). Đúng
b) Tần số của dao động là 1 (Hz). Đúng
c) Quãng đường vật đi được sau 10s là 400 m. Sai
d) Sau 5s vật đi qua vị trí có li độ \(x = 5\left( {cm} \right)\)là 10 lần. Đúng
Cho con lắc lò xo dao động trên mặt phẳng nằm ngang không ma sát như trong hình. Con lắc lò xo thực hiện mỗi dao động mất 2,4 s. Tại t = 0, vật bắt đầu dao động từ chỗ cách vị trí cân bằng x = 3 cm.

a) Chu kì dao động của con lắc là 24s.
b) Tại thời điểm \(t = 0,6s\)vật đang ở VTCB.
c) Tại \(x = 1,5\left( {cm} \right)\)vật có động năng bằng 3 lần thế năng.
d) Thời gian kể từ lúc bắt đầu dao động đến lúc vật đi qua vị trí có li độ \(x = 1,5\sqrt 2 \left( {cm} \right)\)lần thứ 2015 là 2417,1s.
a) Chu kì dao động của con lắc là 24s.
b) Tại thời điểm \(t = 0,6s\)vật đang ở VTCB.
c) Tại \(x = 1,5\left( {cm} \right)\)vật có động năng bằng 3 lần thế năng.
d) Thời gian kể từ lúc bắt đầu dao động đến lúc vật đi qua vị trí có li độ \(x = 1,5\sqrt 2 \left( {cm} \right)\)lần thứ 2015 là 2417,1s.
Vận dụng kiến thức về con lắc lò xo
a) Chu kì dao động của con lắc là 2,4s. Sai
b) Tại thời điểm \(t = 0,6s\)vật đang ở VTCB. Đúng
c) Tại \(x = 1,5\left( {cm} \right)\)vật có động năng bằng 3 lần thế năng. Đúng
d) Thời gian kể từ lúc bắt đầu dao động đến lúc vật đi qua vị trí có li độ \(x = 1,5\sqrt 2 \left( {cm} \right)\)lần thứ 2015 là 2417,1s. Đúng
Vận dụng kiến thức về phương trình li độ
\(x = 5\cos \left( {4\pi t + \frac{\pi }{2}} \right) = 5\cos \left( {4\pi .2,5 + \frac{\pi }{2}} \right) = 0\)
Đáp án: 0
Vận dụng kiến thức về hệ thức độc lập thời gian
\(\begin{array}{l}{A^2} = x_1^2 + \frac{{v_1^2}}{{{\omega ^2}}} = {2^2} + \frac{{{{\left( {4\pi \sqrt 3 } \right)}^2}}}{{{\omega ^2}}}\\{A^2} = x_2^2 + \frac{{v_2^2}}{{{\omega ^2}}} = {\left( {2\sqrt 2 } \right)^2} + \frac{{{{\left( {4\pi \sqrt 2 } \right)}^2}}}{{{\omega ^2}}}\\ \Rightarrow A = 4cm\end{array}\)
Đáp án: 4
Vận dụng kiến thức về công thức tính chu kì
\({a_{\max }} = A{\omega ^2} \Rightarrow 20{\pi ^2} = 5{\omega ^2} \Rightarrow \omega = 2\pi \Rightarrow T = 1s\)
Đáp án: 1
Vận dụng kiến thức về phương trình li độ
\({\rm{\Delta }}t = \frac{2}{{21}} - \frac{1}{{42}} = \frac{1}{{14}} \approx 0,07\,{\rm{s}}\)
Đáp án: 0,07
Vận dụng kiến thức về đường tròn lượng giác
\(t = 999T + \frac{T}{6} = 200s\)
Đáp án: 200
Vận dụng kiến thức về con lắc lò xo
PT dao động có dạng: \(x = \;Acos\left( {\omega t\; + \;\varphi } \right) \Rightarrow x = Acos\left( {\frac{\pi }{2}} \right)\;\)
Vật qua VTCB => tốc độ cực đại của vật là \({v_{max}} = \;20\sqrt 3 \;cm/s\)
Mặt khác \({v_{\max }} = A\omega \Rightarrow A = \frac{{20\sqrt 3 }}{\pi }cm\)
Khi li độ x = 3π cm thì động năng của vật \({W_d} = \frac{1}{2}k({A^2} - {x^2}) = 0,03J\)
Đáp án: 0,03