Đề thi giữa học kì 1 Vật lí 11 Chân trời sáng tạo - Đề số 6 — Không quảng cáo

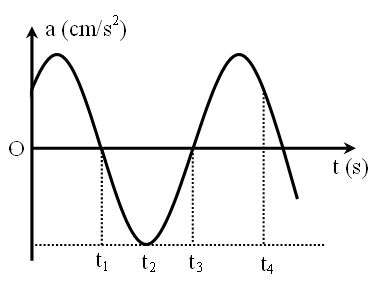
a) Tại thời điểm \({t_1}\), chất điểm đi qua vị trí cân bằng.

b) Tại thời điểm \({t_4}\), chất điểm đang chuyển động nhanh dần theo chiều dương.

c) Tại thời điểm ban đầu, chất điểm đang chuyển động theo chiều dương

d) Chu kì dao động có giá trị \(T = 2\left( {{t_3} - {t_2}} \right)\)..

a) Quỹ đạo dao động của con lắc dài 20 cm

b) Thời gian con lắc đi được quãng đường 40 cm bằng 1 s

c) Trong một chu kì dao động, động năng bằng thế năng 4 lần

d) Thời gian giữa hai lần liên tiếp động năng bằng thế năng là 1 s.

a) Chu kì của con lắc đơn là 0,22 s.

b) Với \({T_s} = 0,22{\rm{ s}}\), ta quan sát thấy con lắc đứng yên tại một chỗ mỗi khi đèn sáng

c) Với \({T_s} = 0,11{\rm{ s}}\), ta có thể quan sát thấy con lắc chỉ xuất hiện ở nhiều nhất là hai vị trí xác định

d) Với \({T_s} = 0,15{\rm{ s}}\), biết rằng lần đầu đèn bật con lắc đi qua vị trí cân bằng theo chiều dương, vào lần chiếu sáng tiếp theo, tỉ số giữa li độ và biên độ của con lắc là 0,65.

a) Tần số dao động riêng của con lắc lò xo là 2,55 Hz.

b) Khối lượng vật nặng là 200 g.

c) Khi thay đổi tần số, biên độ dao động lúc đầu tăng lên sau đó giảm đi.

d) Khi dao động cưỡng bức ổn định, nếu thay đổi pha ban đầu của lực cưỡng bức thì biên độ dao động không thay đổi.

Vận dụng kiến thức về dao động điều hòa - dao động với biên độ không đổi và có tần số xác định, không bị ảnh hưởng bởi lực cản.

Dao động của con lắc lò xo trên mặt bàn không có ma sát là một ví dụ của dao động điều hòa vì có lực hồi phục phụ thuộc vào độ dãn của lò xo (tuân theo định luật Hooke), tần số dao động không thay đổi, và không có ma sát làm giảm biên độ.

Đáp án: A

Vận dụng kiến thức về định luật Hooke và lực đàn hồi của lò xo.

Theo định luật Hooke, lực đàn hồi của lò xo chỉ phụ thuộc vào độ cứng (hệ số đàn hồi) của lò xo và độ dãn của nó, không phụ thuộc vào khối lượng của vật nặng. Do đó, câu B là sai.

Đáp án: B

Vận dụng kiến thức về dao động của con lắc lò xo và mối quan hệ giữa thế năng và lực đàn hồi.

Thế năng của quả cầu đạt cực đại khi biên độ dao động lớn nhất, khi đó lực đàn hồi của lò xo cũng lớn nhất. Phát biểu "khi thế năng của quả cầu lớn nhất thì lực đàn hồi có độ lớn nhỏ nhất" là sai.

Đáp án: B

Vận dụng kiến thức về mối quan hệ giữa gia tốc và li độ trong dao động điều hòa

Trong dao động điều hòa, gia tốc có giá trị tỷ lệ nghịch với li độ và hướng về vị trí cân bằng. Đồ thị gia tốc theo li độ là một đoạn thẳng dốc xuống.

Đáp án: D

Vận dụng kiến thức về tần số dao động của con lắc đơn và sự phụ thuộc vào các yếu tố

Tần số dao động của con lắc đơn chỉ phụ thuộc vào chiều dài dây treo và gia tốc trọng trường, không phụ thuộc vào khối lượng vật nặng.

Đáp án: C

Vận dụng kiến thức về pha ban đầu trong dao động điều hòa

Pha ban đầu cho biết trạng thái ban đầu của dao động, bao gồm vị trí và hướng di chuyển của vật tại thời điểm ban đầu.

Đáp án: A

Vận dụng kiến thức về dao động tắt dần và sự thay đổi của các dạng năng lượng.

Dao động tắt dần là dao động có biên độ giảm dần theo thời gian do ma sát. Do đó, cơ năng và cả động năng lẫn thế năng đều giảm dần. Phát biểu "dao động tắt dần có động năng giảm dần còn thế năng biến thiên điều hòa" là sai.

Đáp án: A

Vận dụng kiến thức về cộng hưởng và đặc điểm của dao động cưỡng bức.

Khi cộng hưởng, tần số của dao động cưỡng bức bằng tần số dao động riêng của hệ, do đó hệ sẽ dao động với tần số dao động riêng.

Đáp án: C

Vận dụng kiến thức về dao động tắt dần và năng lượng duy trì dao động.

Để duy trì dao động ổn định, năng lượng cần cung cấp phải bằng đúng lượng năng lượng mất đi do ma sát trong mỗi chu kỳ, tức là 0,01 J.

Đáp án: C

Vận dụng kiến thức về chu kì dao động

\(T = 2\pi \sqrt {\frac{l}{g}}  = 2\pi \sqrt {\frac{{1,21}}{{{\pi ^2}}}}  = 2,2{\rm{ s}}\)

Đáp án: D

Vận dụng kiến thức về chu kỳ dao động của con lắc đơn và sự phụ thuộc vào khối lượng.

Chu kỳ dao động của con lắc đơn chỉ phụ thuộc vào chiều dài dây và gia tốc trọng trường, không phụ thuộc vào khối lượng của vật. Vì vậy, khi tăng khối lượng lên gấp bốn lần, chu kỳ không thay đổi.

Đáp án: D

Vận dụng kiến thức về con lắc đơn

\(\frac{{{T_2}}}{{{T_1}}} = \sqrt {\frac{{{l_2}}}{{{l_1}}}}  = 0,8 \Rightarrow {l_2} = 0,{8^2}{l_1} = 0,{8^2}.150 = 96{\rm{ cm}}\)

Đáp án: B

Vận dụng kiến thức về phương trình dao động

\({\varphi _{(t = 2{\rm{ s}})}} = \pi .2 + \frac{\pi }{4} = \frac{{9\pi }}{4}{\rm{ rad}}\)

Đáp án: B

Vận dụng kiến thức về phương trình dao động

\[\left| {\left( { - A} \right) - x} \right| = \left| { - 4 - 4\cos \left( {\pi .\frac{1}{2} + \frac{\pi }{4}} \right)} \right| = 4 - 2\sqrt 2 {\rm{ cm}}\]

Đáp án: C

Vận dụng kiến thức về gia tốc trọng trường

\(T = \frac{{42,92 \pm 0,01}}{{20}}\;{\rm{ s}}\)

\(\bar g = 4{{\rm{\pi }}^2}\frac{{\bar l}}{{{{\bar T}^2}}} = 4.{\left( {3.14} \right)^2}\frac{{1,15}}{{{{\left( {42,92 \div 20} \right)}^2}}} = 9,58\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}\)

\({\rm{\Delta }}g = \bar g\left( {\frac{{{\rm{\Delta }}l}}{{\bar l}} + \frac{{{\rm{\Delta }}T}}{{\bar T}}} \right) = 9,58.\left( {\frac{{0,01}}{{1,15}} + \frac{{0,01:20}}{{42,9:20}}} \right) = 0,09\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}{\rm{\;}}\)

Đáp án: A

Vận dụng kiến thức về con lắc là xo

\[n = \frac{{{T_{{\rm{n\'e n}}}}}}{T} = \frac{{2{\rm{\alpha }}}}{{2{\rm{\pi }}}} = \frac{{{{\cos }^{ - 1}}\left( {\frac{{{\rm{\Delta }}{l_0}}}{A}} \right)}}{{\rm{\pi }}} = \frac{{{{\cos }^{ - 1}}\left( {0,5} \right)}}{{\rm{\pi }}} = \frac{1}{3}\]

Đáp án: B

Vận dụng kiến thức về năng lượng dao động

\({A_n} = {\left( {1 - 0,15} \right)^n}{A_0} \to {W_n} = {\left( {{{\left( {1 - 0,15} \right)}^2}} \right)^n}{W_0}\)

\( \Rightarrow {\rm{\Delta }}W = {W_0} - {W_3} = \left( {1 - {{\left( {1 - 0,15} \right)}^{2.3}}} \right){W_0} \approx 0,623.\left( {\frac{1}{2}m\frac{{4{{\rm{\pi }}^2}}}{{{T^2}}}A_0^2} \right) \approx 0,623.\left( {\frac{1}{2}.0,5.\frac{{4{{\rm{\pi }}^2}}}{{0,{2^2}}}.0,{{02}^2}} \right) = 0,061{\rm{ }}\;{\rm{J}}\)

Đáp án: D

Vận dụng kiến thức về phương trình dao động

\(\begin{array}{l}\alpha  =  - {\cos ^{ - 1}}\left( {\frac{x}{A}} \right) + k2\pi  =  - {\cos ^{ - 1}}\left( { - \frac{{5\sqrt 2 }}{{10}}} \right) + k2\pi  = \frac{{ - 3\pi }}{4} + k2\pi \\ \Rightarrow 5\pi t + \frac{\pi }{2} = \frac{{ - 3\pi }}{4} + k2\pi  \Rightarrow t = \frac{{ - 1}}{4} + k\frac{2}{5}\end{array}\)

Lần thứ 2025: \(k = 2025 \Rightarrow t = \frac{{ - 1}}{4} + 2025.\frac{2}{5} = \frac{{3239}}{4}{\rm{ s}}\)

Đáp án: B

a) Tại thời điểm \({t_1}\), chất điểm đi qua vị trí cân bằng.

b) Tại thời điểm \({t_4}\), chất điểm đang chuyển động nhanh dần theo chiều dương.

c) Tại thời điểm ban đầu, chất điểm đang chuyển động theo chiều dương

d) Chu kì dao động có giá trị \(T = 2\left( {{t_3} - {t_2}} \right)\)..

Vận dụng kiến thức về dao động điều hòa

a) \(a = 0 \Rightarrow x = 0\). Vật đi qua vị trí cân bằng.→ a đúng

b) Gia tốc dương và đang giảm, suy ra li độ âm và đang tăng. Suy ra chất điểm đang chuyển động nhanh dần theo chiều dương. → b đúng

c) Ban đầu, gia tốc dương và đang tăng, suy ra li độ âm và đang giảm. Suy ra chất điểm chuyển động theo chiều âm. → c sai

d) Chu kì dao động có giá trị \(T = 2\left( {{t_3} - {t_2}} \right)\).→ d đúng

a) Quỹ đạo dao động của con lắc dài 20 cm

b) Thời gian con lắc đi được quãng đường 40 cm bằng 1 s

c) Trong một chu kì dao động, động năng bằng thế năng 4 lần

d) Thời gian giữa hai lần liên tiếp động năng bằng thế năng là 1 s.

Vận dụng kiến thức về con lắc lò xo

a) \(L = 2{\rm{A}} = 2.20 = 40{\rm{ cm}}\)→ a sai

b) Cứ nửa chu kì chất điểm đi được 2A. → b đúng

c) \({W_d} = {W_t} \Rightarrow {A^2} - {x^2} = {x^2} \Rightarrow {x^2} = \frac{{{A^2}}}{2} \Rightarrow x =  \pm \frac{{A\sqrt 2 }}{2}\)

Mà một chu kì vật đi qua bất kì li độ x 2 lần nên trong một chu kì dao động, động năng bằng thế năng 4 lần. → c đúng

d) \(x =  \pm \frac{{A\sqrt 2 }}{2} \Rightarrow \alpha  \in \left\{ {\frac{\pi }{4};\frac{{3\pi }}{4};\frac{{ - \pi }}{4};\frac{{ - 3\pi }}{4}} \right\} \Rightarrow \Delta t = \frac{T}{4} = \frac{2}{4} = 0,5{\rm{ s}}\)→ d sai

a) Chu kì của con lắc đơn là 0,22 s.

b) Với \({T_s} = 0,22{\rm{ s}}\), ta quan sát thấy con lắc đứng yên tại một chỗ mỗi khi đèn sáng

c) Với \({T_s} = 0,11{\rm{ s}}\), ta có thể quan sát thấy con lắc chỉ xuất hiện ở nhiều nhất là hai vị trí xác định

d) Với \({T_s} = 0,15{\rm{ s}}\), biết rằng lần đầu đèn bật con lắc đi qua vị trí cân bằng theo chiều dương, vào lần chiếu sáng tiếp theo, tỉ số giữa li độ và biên độ của con lắc là 0,65.

Vận dụng kiến thức về con lắc đơn

a) . \(T = 2\pi \sqrt {\frac{l}{g}}  = 2\pi \sqrt {\frac{{0,0121}}{{{\pi ^2}}}}  = 0,22{\rm{ s}}{\rm{.}}\)→ a đúng

b) Vì \({T_s} = T\), mỗi lần đèn sáng con lắc lặp lại trạng thái dao động. → b đúng

c) Vì \({T_s} = \frac{T}{2}\), ở lần đèn sáng tiếp theo, con lắc có pha dao động tăng thêm 1\(\pi \) , vì vậy nó sẽ lặp lại xen kẽ giữa li độ \(\alpha \) và \( - \alpha \). Trừ trường hợp \(\alpha  = 0\) thì con lắc chỉ được quan sát thấy có 1 li độ. → c đúng

d) \(\frac{\alpha }{{{\alpha _0}}} = \cos \left( {\frac{{2\pi }}{T}{T_s} + \varphi } \right) = \cos \left( {\frac{{2\pi }}{{0,22}}.0,15 - \frac{\pi }{2}} \right) \approx 0,91\).→ d sai

a) Tần số dao động riêng của con lắc lò xo là 2,55 Hz.

b) Khối lượng vật nặng là 200 g.

c) Khi thay đổi tần số, biên độ dao động lúc đầu tăng lên sau đó giảm đi.

d) Khi dao động cưỡng bức ổn định, nếu thay đổi pha ban đầu của lực cưỡng bức thì biên độ dao động không thay đổi.

Vận dụng kiến thức về con lắc lò xo

a) Tại giá trị tần số của ngoại lực bằng tần số riêng của vật thì vật dao động với biên độ cực đại nên tần số dao động riêng của con lắc lò xo là 2,55 Hz. → a đúng

b) \(\omega  = 2\pi f = \sqrt {\frac{k}{m}}  \Rightarrow m = \frac{k}{{{{\left( {2\pi f} \right)}^2}}} = \frac{{64}}{{{{(2\pi .2,55)}^2}}} \approx 0,25{\rm{ kg}} = 250{\rm{ g}}\)→ b sai

c) Khi thay đổi tần số, biên độ dao động lúc đầu tăng lên sau đó giảm đi. → c đúng

d) Biên độ dao động không phụ thuộc vào pha ban đầu của lực cưỡng bức. → d đúng

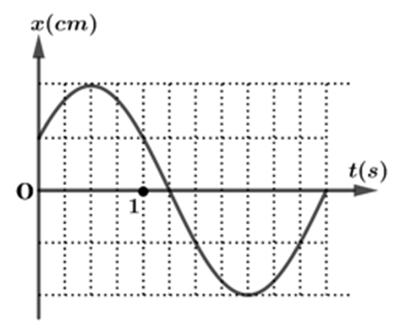
Vận dụng kiến thức về dao động điều hòa

Nửa chu kì là 6 ô, suy ra chu kì là 12 ô. Thấy 1 s tương ướng với 4 ô. Suy ra chu kì là 3 s.

Đáp án: 3

Vận dụng kiến thức về hiện tượng cộng hưởng

Nước sóng sánh mạnh nhất suy ra có sự cộng hưởng, chu kì bước chân bằng chu kì riêng.

\(T = \frac{L}{v} = \frac{{0,5}}{{{{2,5} \mathord{\left/

{\vphantom {{2,5} {3,6}}} \right.

\kern-\nulldelimiterspace} {3,6}}}} = 0,72{\rm{ s}}\)

Đáp án: 0,72

Vận dụng kiến thức về phương trình li độ

\({v_{{\rm{max}}}} = \frac{{{a_{\max }}}}{\omega } = \frac{{80}}{4} = 20{\rm{ cm/s}}\)

Đáp án: 20

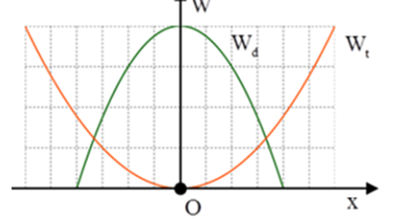
Vận dụng kiến thức về năng lượng dao động

\({W_{{d_{{\rm{max}}}}}} = {W_{{t_{{\rm{max}}}}}} \Rightarrow {W_1} = {W_2} \Rightarrow {m_1}A_1^2 = {m_2}A_2^2 \Rightarrow \frac{{{m_1}}}{{{m_2}}} = {\left( {\frac{{{A_2}}}{{{A_1}}}} \right)^2} = {\left( {\frac{6}{4}} \right)^2} = 2,25\)

Đáp án: 2,25

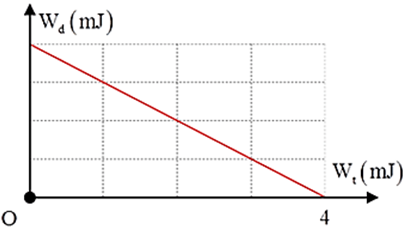
Vận dụng kiến thức về động năng

\(\omega  = \sqrt {\frac{{2W}}{{m{A^2}}}}  = \sqrt {\frac{{{{2.4.10}^{ - 3}}}}{{0,1{{\left( {{{0,08} \mathord{\left/

{\vphantom {{0,08} 2}} \right.

\kern-\nulldelimiterspace} 2}} \right)}^2}}}}  \approx 3,87{\rm{ rad/s}}\)

Đáp án: 3,87

Vận dụng kiến thức về phương trình dao động

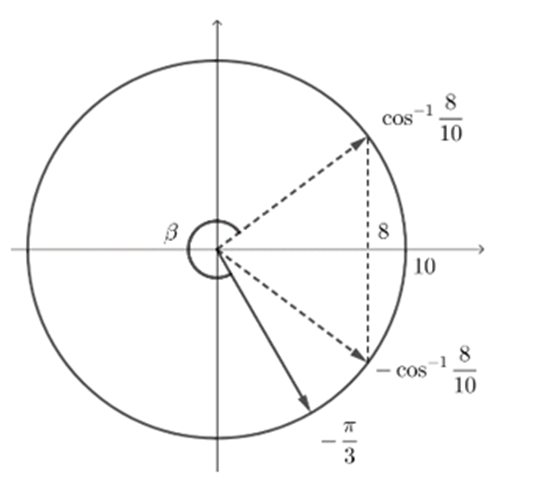
\[t = 8T - \frac{\beta }{\omega } = 8.\frac{{2\pi }}{{3\pi }} - \frac{{2\pi  - \left( {{{\cos }^{ - 1}}\left( {0,8} \right) + \frac{\pi }{3}} \right)}}{{3\pi }} \approx 4,85{\rm{ s}}\]

Đáp án: 4,85