Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 10
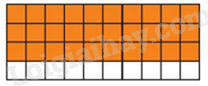
Phần trắc nghiệm (3 điểm) Câu 1 (NB): Phân số nào dưới đây không biểu diễn phần tô màu cam trong hình bên:
Đề bài
-
A.
\(\frac{{30}}{{40}}\)
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{3}{4}\)
-
D.
\(\frac{6}{8}\)
Giá trị \(\frac{3}{4}\) của – 60 là:
-
A.
80.
-
B.
- 80.
-
C.
45.
-
D.
- 45.
Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi
-
A.
\(a.3 = b.4\).
-
B.
\(a.4 = 3.b\).
-
C.
\(a + 4 = b + 3\).
-
D.
\(a - 4 = b - 3\).
Khi rút gọn phân \(\frac{{ - 27}}{{63}}\) ta được phân số tối giản là số nào sau đây?
-
A.
\(\frac{9}{{21}}\).
-
B.
\(\frac{{ - 3}}{7}\).
-
C.
\(\frac{3}{7}\).
-
D.
\(\frac{{ - 9}}{{21}}\).
Cho bảng dự báo thời tiết 10 ngày tới của Thủ đô Hà Nội.
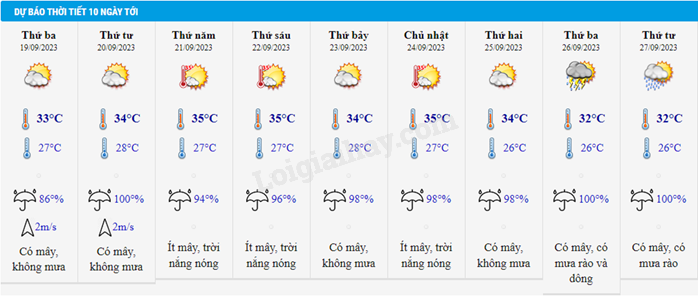
Trong bảng trên, những ngày ít mây, trời nắng nóng là:
-
A.
Thứ ba, thứ năm, chủ nhật.
-
B.
Thứ hai, thứ sáu, chủ nhật.
-
C.
Thứ tư, thứ bảy, chủ nhật.
-
D.
Thứ năm, thứ sáu, chủ nhật.
Biểu đồ dưới đây biểu diễn số học sinh nam và nữ của các lớp khối 6 của một trường THCS.
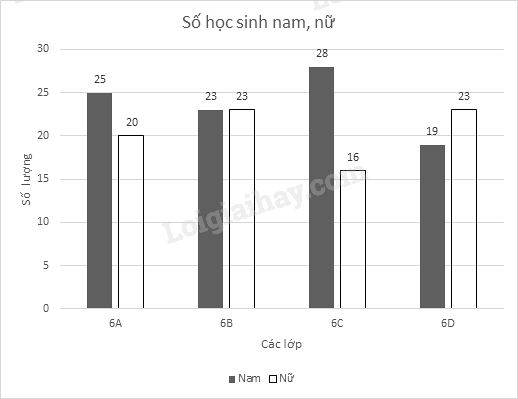
Lớp có số học sinh nữ ít nhất là
-
A.
lớp 6A.
-
B.
lớp 6B.
-
C.
lớp 6C.
-
D.
lớp 6D.
Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; các quả bóng có kích thước và khối lượng như nhau. Mỗi lần Sơn lấy 1 quả bóng ra và ghi lại màu của quả bóng sau đó lại bỏ bóng vào hộp. Sau 20 lần liên tiếp lấy bóng, có 5 lần xuất hiện màu đỏ, 7 lần xuất hiện màu vàng. Tính xác suất thực nghiệm xuất hiện màu xanh.
-
A.
\(\frac{1}{5}\).
-
B.
\(\frac{3}{4}\).
-
C.
\(\frac{2}{5}\).
-
D.
\(\frac{7}{{20}}\).
Trong hộp có 4 thẻ đánh số 1; 2; 3; 4. Hoa lấy ngẫu nhiên một thẻ từ hộp, ghi số lại rồi trả lại hộp. Lặp lại hoạt động trên 20 lần, Hoa được kết quả như sau:

Xác suất thực nghiệm của sự kiện Hoa lấy được thẻ ghi số nguyên tố chẵn là:
-
A.
\(\frac{7}{{20}}\).
-
B.
\(\frac{4}{{20}}\).
-
C.
\(\frac{5}{{20}}\).
-
D.
\(\frac{3}{{20}}\).
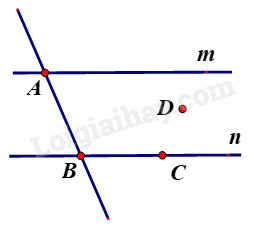
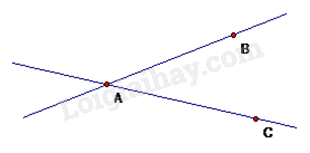
-
A.
Điểm A.
-
B.
Điểm B và điểm C.
-
C.
Điểm B và điểm D.
-
D.
Điểm D và điểm C.
Cho F là điểm nằm giữa hai điểm P và Q. Khi đó tia đối của tia FQ là
-
A.
tia QF.
-
B.
tia QP.
-
C.
tia FP.
-
D.
tia PF.
Em hãy chọn câu đúng.
-
A.
Qua hai điểm phân biệt có vô số đường thẳng.
-
B.
Có vô số điểm cùng thuộc một đường thẳng.
-
C.
Hai đường thẳng phân biệt thì song song.
-
D.
Trong ba điểm thẳng hàng thì có hai điểm nằm giữa.
-
A.
Hai đường thẳng AB và AC cắt nhau.
-
B.
Hai đường thẳng AB và AC song song với nhau.
-
C.
Hai đường thẳng AB và AC trùng nhau.
-
D.
Hai đường thẳng AB và AC có hai điểm chung.
Lời giải và đáp án
-
A.
\(\frac{{30}}{{40}}\)
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{3}{4}\)
-
D.
\(\frac{6}{8}\)
Đáp án : B
Quan sát hình vẽ và tìm các phân số bằng với phân số đó..
Ta thấy trong hình có 40 ô và có 30 ô màu cam nên ta có phân số biểu diễn phần tô màu cam trong hình bên là \(\frac{{30}}{{40}}\).
Các phân số bằng với phân số \(\frac{{30}}{{40}}\) là \(\frac{3}{4}\) và \(\frac{6}{8}\).
Vậy phân số không biểu diễn là phân số \(\frac{1}{4}\).
Đáp án B.
Giá trị \(\frac{3}{4}\) của – 60 là:
-
A.
80.
-
B.
- 80.
-
C.
45.
-
D.
- 45.
Đáp án : D
Tính \(\frac{m}{n}\) của a bằng \(a.\frac{m}{n}\).
Giá trị \(\frac{3}{4}\) của – 60 là: \(\left( { - 60} \right).\frac{3}{4} = - 45\).
Đáp án D.
Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi
-
A.
\(a.3 = b.4\).
-
B.
\(a.4 = 3.b\).
-
C.
\(a + 4 = b + 3\).
-
D.
\(a - 4 = b - 3\).
Đáp án : B
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) khi \(ad = bc\).
Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi \(a.4 = 3.b\) .
Đáp án B.
Khi rút gọn phân \(\frac{{ - 27}}{{63}}\) ta được phân số tối giản là số nào sau đây?
-
A.
\(\frac{9}{{21}}\).
-
B.
\(\frac{{ - 3}}{7}\).
-
C.
\(\frac{3}{7}\).
-
D.
\(\frac{{ - 9}}{{21}}\).
Đáp án : B
Sử dụng quy tắc rút gọn phân số.
\(\frac{{ - 27}}{{63}} = \frac{{ - 27:9}}{{63:9}} = \frac{{ - 3}}{7}\).
Đáp án B.
Cho bảng dự báo thời tiết 10 ngày tới của Thủ đô Hà Nội.

Trong bảng trên, những ngày ít mây, trời nắng nóng là:
-
A.
Thứ ba, thứ năm, chủ nhật.
-
B.
Thứ hai, thứ sáu, chủ nhật.
-
C.
Thứ tư, thứ bảy, chủ nhật.
-
D.
Thứ năm, thứ sáu, chủ nhật.
Đáp án : D
Quan sát bảng số liệu để trả lời.
Trong bảng trên, những ngày ít mây, trời nắng nóng là thứ năm, thứ sáu, chủ nhật.
Đáp án D.
Biểu đồ dưới đây biểu diễn số học sinh nam và nữ của các lớp khối 6 của một trường THCS.

Lớp có số học sinh nữ ít nhất là
-
A.
lớp 6A.
-
B.
lớp 6B.
-
C.
lớp 6C.
-
D.
lớp 6D.
Đáp án : C
Quan sát biểu đồ và trả lời.
Lớp có số học sinh nữ ít nhất là lớp 6C.
Đáp án C.
Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ, 1 quả bóng vàng; các quả bóng có kích thước và khối lượng như nhau. Mỗi lần Sơn lấy 1 quả bóng ra và ghi lại màu của quả bóng sau đó lại bỏ bóng vào hộp. Sau 20 lần liên tiếp lấy bóng, có 5 lần xuất hiện màu đỏ, 7 lần xuất hiện màu vàng. Tính xác suất thực nghiệm xuất hiện màu xanh.
-
A.
\(\frac{1}{5}\).
-
B.
\(\frac{3}{4}\).
-
C.
\(\frac{2}{5}\).
-
D.
\(\frac{7}{{20}}\).
Đáp án : C
Xác suất thực nghiệm xuất hiện màu A khi lấy nhiều lần bằng tỉ số giữa số lần màu A xuất hiện với tổng số lần lấy.
Xác suất thực nghiệm xuất hiện màu xanh là: \(\frac{{20 - 5 - 7}}{{20}} = \frac{8}{{20}} = \frac{2}{5}\).
Đáp án C.
Trong hộp có 4 thẻ đánh số 1; 2; 3; 4. Hoa lấy ngẫu nhiên một thẻ từ hộp, ghi số lại rồi trả lại hộp. Lặp lại hoạt động trên 20 lần, Hoa được kết quả như sau:

Xác suất thực nghiệm của sự kiện Hoa lấy được thẻ ghi số nguyên tố chẵn là:
-
A.
\(\frac{7}{{20}}\).
-
B.
\(\frac{4}{{20}}\).
-
C.
\(\frac{5}{{20}}\).
-
D.
\(\frac{3}{{20}}\).
Đáp án : B
Xác suất thực nghiệm xuất hiện thẻ A khi lấy nhiều lần bằng tỉ số giữa số lần thẻ A xuất hiện với tổng số lần lấy.
Số nguyên tố chẵn duy nhất là số 2 nên tổng số lần lấy được thẻ ghi số nguyên tố chẵn là 4.
Xác suất thực nghiệm của sự kiện Hoa lấy được thẻ ghi số nguyên tố chẵn là: \(\frac{4}{{20}}\).
Đáp án B.
-
A.
Điểm A.
-
B.
Điểm B và điểm C.
-
C.
Điểm B và điểm D.
-
D.
Điểm D và điểm C.
Đáp án : B
Quan sát hình vẽ để trả lời.
Đường thẳng n đi qua điểm B và điểm C
Đáp án B.
Cho F là điểm nằm giữa hai điểm P và Q. Khi đó tia đối của tia FQ là
-
A.
tia QF.
-
B.
tia QP.
-
C.
tia FP.
-
D.
tia PF.
Đáp án : C
Dựa vào kiến thức về tia đối.
Tia đối của tia FQ là tia FP (vì F nằm giữa P và Q).
Đáp án C.
Em hãy chọn câu đúng.
-
A.
Qua hai điểm phân biệt có vô số đường thẳng.
-
B.
Có vô số điểm cùng thuộc một đường thẳng.
-
C.
Hai đường thẳng phân biệt thì song song.
-
D.
Trong ba điểm thẳng hàng thì có hai điểm nằm giữa.
Đáp án : B
Dựa vào kiến thức về đường thẳng.
Qua hai điểm phân biệt chỉ có 1 đường thẳng nên A sai.
Có vô số điểm cùng thuộc một đường thẳng. nên B đúng.
Hai đường thẳng phân biết chưa chắc đã song song nên C sai.
Trong ba điểm thẳng hàng chỉ có một điểm nằm giữa nên D sai.
Đáp án B.
-
A.
Hai đường thẳng AB và AC cắt nhau.
-
B.
Hai đường thẳng AB và AC song song với nhau.
-
C.
Hai đường thẳng AB và AC trùng nhau.
-
D.
Hai đường thẳng AB và AC có hai điểm chung.
Đáp án : A
Quan sát hình vẽ để xác định.
Hai đường thẳng AB và AC cắt nhau tại A.
Đáp án A.
Dựa vào quy tắc tính với phân số.
a) \(\frac{{ - 3}}{7} + \frac{5}{7} = \frac{2}{7}\)
b) \(\frac{2}{3} + \frac{{ - 3}}{5} = \frac{{10}}{{15}} + \frac{{ - 9}}{{15}} = \frac{1}{{15}}\)
c) \(\frac{2}{9} - \left( {\frac{1}{{20}} + \frac{2}{9}} \right) = \frac{2}{9} - \frac{1}{{20}} - \frac{2}{9} = - \frac{1}{{20}}\)
d) \(\frac{{11}}{{23}}.\frac{{12}}{{17}} + \frac{{11}}{{23}}.\frac{5}{{17}} + \frac{{12}}{{23}}\)\( = \frac{{11}}{{23}}.\left( {\frac{{12}}{{17}} + \frac{5}{{17}}} \right) + \frac{{12}}{{23}}\) \( = \frac{{11}}{{23}} \cdot 1 + \frac{{12}}{{23}}\)\( = \frac{{23}}{{23}}\)\( = 1\)
Quan sát bảng số liệu để trả lời câu hỏi.
a) Đối tượng thống kê: học sinh lớp 6A.
Tiêu chí thống kê: cỡ áo của từng học sinh.
b) Cỡ áo 34 có: 3 học sinh Cỡ áo 35 có: 11 học sinh Cỡ áo 36 có: 13 học sinh Cỡ áo 38 có: 3 học sinh Tổng số cỡ áo 35và 36 phải may nhiều hơn số tổng số cỡ áo 34 và 35 là: (11 + 13) – (3 + 3) = 18 (áo) Vậy thông báo đó của nhân viên là
Áp dụng cách tính \(\frac{m}{n}\) của a bằng \(a.\frac{m}{n}\).
Số gạo ngày thứ hai bán được là: \(\frac{4}{9}.\left( {1 - \frac{1}{3}} \right) = \frac{8}{{27}}\) (tổng số gạo)
1400kg gạo tương ứng với phân số \(1 - \frac{1}{3} - \frac{8}{{27}} = \frac{{10}}{{27}}\) (tổng số gạo).
Số gạo bán được trong 3 ngày là: \(1400:\frac{{10}}{{27}} = 3780\) (kg)
Vậy số gạo bán được trong cả ba ngày là 3780kg.
Vẽ hình theo yêu cầu.
a) Chứng minh OA < OB nên A nằm giữa O và B.
b) Tính KA dựa vào KO và OA. So sánh KA và AB.

a) Trên tia Ox ta có OA = 3cm, OB = 6cm vì 3 < 6 nên OA < OB
Do đó A nằm giữa O và B. (1)
Suy ra: OA + AB = OB
Thay số ta được 3 + AB = 6
Suy ra AB = 3(cm)
Mà OA = 3(cm) nên OA = AB (2)
Từ (1) và (2) suy ra: A là trung điểm của OB (đpcm)
b) Ta có A thuộc tia Ox, K thuộc tia đối của tia Ox nên A và K nằm khác phía đối với O hay O nằm giữa K và A.
Suy ra KO + OA = KA.
Thay số ta được 1 + 3 = KA
Suy ra KA = 4(cm).
Mà AB = 3cm nên KA > AB (do 4 > 3).
Vậy KA > AB.
Tính số ngày không có bạn nào đi muộn, số ngày có bạn đi muộn.
Xác suất thực nghiệm của sự kiện bằng tỉ số giữa số ngày xảy ra sự kiện với tổng số ngày.
a) Số ngày không có bạn nào đi học muộn trong 20 ngày là 10. Vậy xác suất thực nghiệm của sự kiện “một ngày không có bạn nào đi học muộn” trong 20 ngày là \(\frac{{10}}{{20}} = \frac{1}{2}\)
b) Số ngày có bạn đi học muộn trong 20 ngày là 10. Vậy xác suất thực nghiệm của sự kiện “một ngày có bạn đi học muộn” trong 20 ngày là \(\frac{{10}}{{20}} = \frac{1}{2}\)
 a) Nêu đối tượng thống kê và tiêu chí thống kê.
b) Nhân viên đo trực tiếp thông báo lại cho chủ cửa hàng rằng tổng số cỡ áo 35 và 36 phải may nhiều hơn số tổng số cỡ áo 34 và 35 là 10 áo. Thông báo đó của nhân viên có đúng không? Vì sao?
a) Nêu đối tượng thống kê và tiêu chí thống kê.
b) Nhân viên đo trực tiếp thông báo lại cho chủ cửa hàng rằng tổng số cỡ áo 35 và 36 phải may nhiều hơn số tổng số cỡ áo 34 và 35 là 10 áo. Thông báo đó của nhân viên có đúng không? Vì sao?
