Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 7
Phần trắc nghiệm (3 điểm) Câu 1 (NB): Trong cách viết sau, cách viết nào cho ta phân số?
Đề bài
Trong cách viết sau, cách viết nào cho ta phân số?
-
A.
\(\frac{4}{7}\).
-
B.
\(\frac{{0,25}}{{ - 3}}\).
-
C.
\(\frac{5}{0}\).
-
D.
\(\frac{{6,23}}{{7,4}}\).
Số đối của phân số \( - \frac{{16}}{{25}}\) là:
-
A.
\(\frac{{16}}{{25}}\).
-
B.
\(\frac{{25}}{{16}}\).
-
C.
\(\frac{6}{8}\).
-
D.
\(\frac{{10}}{{75}}\).
Phân số nào sau đây bằng phân số \(\frac{3}{4}\)?
-
A.
\(\frac{{13}}{{20}}\).
-
B.
\(\frac{3}{9}\).
-
C.
\(\frac{6}{8}\).
-
D.
\(\frac{{10}}{{75}}\).
Tìm số nguyên \(y\) biết \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\).
-
A.
\(2\).
-
B.
\(6\).
-
C.
\(3\).
-
D.
\(9\).
Trong trò chơi “Hộp quà bí mật”, có 5 hộp quà giống nhau về kích thước và màu sắc, mỗi chiếc hộp chứa một phần thưởng khác nhau gồm: 1 bông hoa, 1 cây bút mực, 1 quyển truyện, 1 quyển vở, 1 cây thước. Lấy ngẫu một hộp quà, hỏi có bao nhiêu kết quả có thể xảy ra với phần quà trong hộp?
-
A.
4.
-
B.
5.
-
C.
6.
-
D.
7.
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Nhơn Khánh.
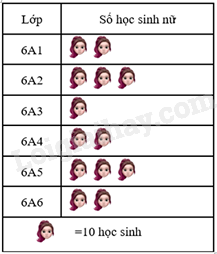
Chọn đáp án đúng
-
A.
Lớp 6A1 có ít học sinh nữ nhất.
-
B.
Lớp 6A4 có nhiều học sinh nữ hơn lớp 6A5.
-
C.
Lớp 6A6 có 20 học sinh nữ.
-
D.
Tổng số học sinh nữ của các khối lớp 6 là 120 học sinh.
Trong cuộc khảo sát về họ của 32 học sinh lớp 6A, giáo viên lập được bảng thống kê như sau:

Hỏi ở lớp 6A, họ nào có nhiều số học sinh nhất?
-
A.
Hoàng.
-
B.
Đỗ.
-
C.
Nguyễn.
-
D.
Trần.
Bạn Sơn tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt \(S\) còn bạn Tùng tung 100 lần và thấy có 55 lần xuất hiện mặt \(S\). Bạn Sơn nói xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{30}}{{50}}\); còn bạn Tùng bảo rằng xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{55}}{{100}}\). Vậy trong hai bạn thì bạn nào nói đúng?
-
A.
Bạn Tùng.
-
B.
Bạn Sơn.
-
C.
Cả hai bạn đều đúng.
-
D.
Cả hai bạn đều sai.
-
A.
1 giao điểm.
-
B.
2 giao điểm.
-
C.
3 giao điểm.
-
D.
4 giao điểm.
-
A.
Chỉ có 1 đường thẳng
-
B.
Không có đường thẳng nào
-
C.
Vô số đường thẳng
-
D.
Có 2 đường thẳng
-
A.
Hai tia \(OA\) và \(OB\) đối nhau.
-
B.
Hai tia \(BA\) và \(OB\) đối nhau.
-
C.
Hai tia \(OA\) và \(BO\) đối nhau.
-
D.
Hai tia \(AB\) và \(OB\) đối nhau.
-
A.
3.
-
B.
4.
-
C.
5.
-
D.
6.
Lời giải và đáp án
Trong cách viết sau, cách viết nào cho ta phân số?
-
A.
\(\frac{4}{7}\).
-
B.
\(\frac{{0,25}}{{ - 3}}\).
-
C.
\(\frac{5}{0}\).
-
D.
\(\frac{{6,23}}{{7,4}}\).
Đáp án : A
Dựa vào khái niệm về phân số.
\(\frac{{0,25}}{{ - 3}}\) không phải phân số vì \(0,25 \notin \mathbb{Z}\).
\(\frac{5}{0}\) không phải phân số vì 0 nằm ở mẫu.
\(\frac{{6,23}}{{7,4}}\) không phải phân số vì \(6,23;7,4 \notin \mathbb{Z}\).
\(\frac{4}{7}\) là phân số vì \(4;7 \in \mathbb{Z};7 \ne 0\).
Đáp án A.
Số đối của phân số \( - \frac{{16}}{{25}}\) là:
-
A.
\(\frac{{16}}{{25}}\).
-
B.
\(\frac{{25}}{{16}}\).
-
C.
\(\frac{6}{8}\).
-
D.
\(\frac{{10}}{{75}}\).
Đáp án : A
Số đối của phân số \(\frac{a}{b}\) là phân số \( - \frac{a}{b}\).
Số đối của phân số \( - \frac{{16}}{{25}}\) là \(\frac{{16}}{{25}}\).
Đáp án A.
Phân số nào sau đây bằng phân số \(\frac{3}{4}\)?
-
A.
\(\frac{{13}}{{20}}\).
-
B.
\(\frac{3}{9}\).
-
C.
\(\frac{6}{8}\).
-
D.
\(\frac{{10}}{{75}}\).
Đáp án : C
Sử dụng quy tắc nhân cả tử và mẫu của một phân số: Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
Ta có: \(\frac{3}{4} = \frac{{3.2}}{{4.2}} = \frac{6}{8}\) nên phân số \(\frac{6}{8} = \frac{3}{4}\).
Đáp án C.
Tìm số nguyên \(y\) biết \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\).
-
A.
\(2\).
-
B.
\(6\).
-
C.
\(3\).
-
D.
\(9\).
Đáp án : D
Hai phân số \(\frac{a}{b} = \frac{c}{d}\) nếu ad = bc.
Ta có: \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\) nên
\(\begin{array}{l}2.\left( { - y} \right) = 6.\left( { - 3} \right)\\ - 2y = - 18\\y = 9\end{array}\)
Đáp án D.
Trong trò chơi “Hộp quà bí mật”, có 5 hộp quà giống nhau về kích thước và màu sắc, mỗi chiếc hộp chứa một phần thưởng khác nhau gồm: 1 bông hoa, 1 cây bút mực, 1 quyển truyện, 1 quyển vở, 1 cây thước. Lấy ngẫu một hộp quà, hỏi có bao nhiêu kết quả có thể xảy ra với phần quà trong hộp?
-
A.
4.
-
B.
5.
-
C.
6.
-
D.
7.
Đáp án : B
Dựa vào mô hình trò chơi lấy ngẫu nhiên.
Có 5 kết quả có thể xảy ra đó là: 1 bông hoa, 1 cây bút mực, 1 quyển truyện, 1 quyển vở, 1 cây thước.
Đáp án B.
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Nhơn Khánh.

Chọn đáp án đúng
-
A.
Lớp 6A1 có ít học sinh nữ nhất.
-
B.
Lớp 6A4 có nhiều học sinh nữ hơn lớp 6A5.
-
C.
Lớp 6A6 có 20 học sinh nữ.
-
D.
Tổng số học sinh nữ của các khối lớp 6 là 120 học sinh.
Đáp án : C
Quan sát biểu đồ để trả lời.
Lớp 6A3 có ít học sinh nữ nhất nên A sai.
Lớp 6A5 có nhiều học sinh nữ hơn lớp 6A4 (30 > 20) nên B sai.
Lớp 6A6 có 20 học sinh nữ nên C đúng (2.10 = 20)
Tổng số học sinh nữ là: 2.10 + 3.10 + 1.10 + 2.10 + 3.10 + 2.10 = 130 nên D sai.
Đáp án C.
Trong cuộc khảo sát về họ của 32 học sinh lớp 6A, giáo viên lập được bảng thống kê như sau:

Hỏi ở lớp 6A, họ nào có nhiều số học sinh nhất?
-
A.
Hoàng.
-
B.
Đỗ.
-
C.
Nguyễn.
-
D.
Trần.
Đáp án : C
Quan sát bảng thống kê để trả lời.
Quan sát bảng thống kê ta thấy họ Nguyễn có nhiều học sinh nhất (12 học sinh).
Đáp án C.
Bạn Sơn tung đồng xu 50 lần thấy có 30 lần xuất hiện mặt \(S\) còn bạn Tùng tung 100 lần và thấy có 55 lần xuất hiện mặt \(S\). Bạn Sơn nói xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{30}}{{50}}\); còn bạn Tùng bảo rằng xác suất thực nghiệm xuất hiện mặt \(S\) là \(\frac{{55}}{{100}}\). Vậy trong hai bạn thì bạn nào nói đúng?
-
A.
Bạn Tùng.
-
B.
Bạn Sơn.
-
C.
Cả hai bạn đều đúng.
-
D.
Cả hai bạn đều sai.
Đáp án : C
Tình huống thực nghiệm khác nhau thì có thể thu được xác suất thực nghiệm khác nhau.
Cả hai bạn đều đúng. Vì mỗi tình huống thực nghiệm sẽ cho một xác suất thực nghiệm (có thể không giống nhau)
Đáp án C.
-
A.
1 giao điểm.
-
B.
2 giao điểm.
-
C.
3 giao điểm.
-
D.
4 giao điểm.
Đáp án : D
Quan sát hình vẽ để trả lời.
Có 4 giao điểm tạo bởi 4 đường thẳng trong hình trên.
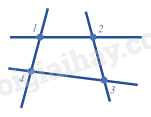
Đáp án D.
-
A.
Chỉ có 1 đường thẳng
-
B.
Không có đường thẳng nào
-
C.
Vô số đường thẳng
-
D.
Có 2 đường thẳng
Đáp án : A
Dựa vào kiến thức về điểm và đường thẳng.
Qua hai điểm phân biệt ta chỉ vẽ được 1 đường thẳng nên A đúng.
Đáp án A.
-
A.
Hai tia \(OA\) và \(OB\) đối nhau.
-
B.
Hai tia \(BA\) và \(OB\) đối nhau.
-
C.
Hai tia \(OA\) và \(BO\) đối nhau.
-
D.
Hai tia \(AB\) và \(OB\) đối nhau.
Đáp án : A
Dựa vào kiến thức về tia.
Hai tia OA và OB là hai tia đối nhau.
Đáp án A.
-
A.
3.
-
B.
4.
-
C.
5.
-
D.
6.
Đáp án : D
Dựa vào kiến thức về đoạn thẳng.
Có 6 đoạn thẳng trong hình vẽ, đó là: KJ, KL, KN, JL, JN, LN.
Đáp án D.
Dựa vào các quy tắc tính với phân số.
a) A = \(\frac{1}{2}\) + \(\frac{1}{3}\) = \(\frac{3}{6} + \frac{2}{6} = \frac{5}{6}\)
b) B = \(\frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}\)\( = \left( {\frac{{ - 3}}{7} - \frac{4}{7}} \right) + \left( {\frac{5}{{14}} + \frac{9}{{14}}} \right) + \frac{3}{{12}}\)\( = - 1 + 1 + \frac{3}{{12}}\) \( = \frac{3}{{12}}\) = \(\frac{1}{4}\)
c) \(C = \frac{{25}}{6}:\frac{5}{3} - \left( {\frac{{ - 1}}{4}} \right)\)\( = \frac{{25}}{6}.\frac{3}{5} + \frac{1}{4}\)\( = \frac{5}{2} + \frac{1}{4}\)\( = \frac{{10}}{4} + \frac{1}{4} = \frac{{11}}{4}\)
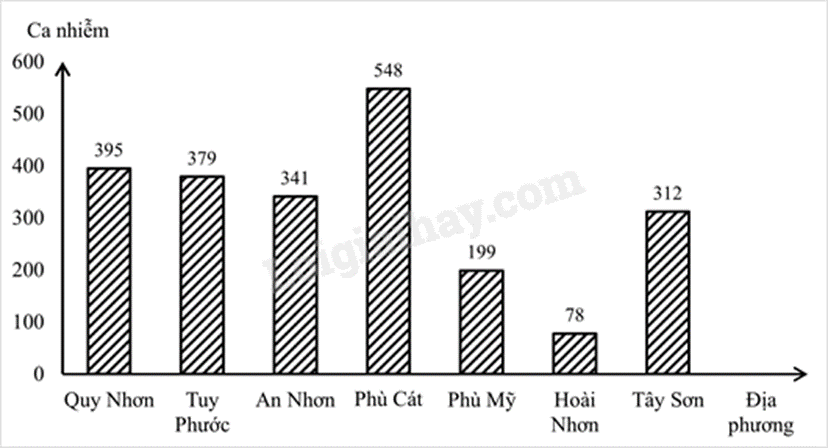
Quan sát biểu đồ để trả lời câu hỏi.
a) Địa phương có số ca nhiễm Covid – 19 là Phù Cát (548 ca nhiễm)
Số ca nhiễm Covid – 19 ở Phù Cát nhiều hơn số ca nhiễm Covid – 19 ở Hoài Nhơn và Tây Sơn là:
\(548 - (78 + 312) = 158\)(Ca nhiễm)
b) Tổng số ca nhiễm Covid – 19 của một số địa phương tại tỉnh Bình Định từ 6h00 ngày 10/3/2022 đến 6h00 ngày 11/3/2022.
\(395 + 379 + 341 + 548 + 199 + 79 + 312 = 2253\)(Ca nhiễm)
a) Xác định các kết quả có thể xảy ra.
b) Xác suất thực nghiệm xuất hiện màu A khi lấy nhiều lần bằng tỉ số giữa số lần màu A xuất hiện với tổng số lần lấy.
a) Có 6 kết quả có thể xảy ra với màu của con Gấu bông được lấy ra, đó là: Đỏ, Xanh, Vàng, Trắng, Hồng, Đen.
Tập hợp các kết quả đối với màu của con Gấu bông được lấy ra là:
{Đỏ, Xanh, Vàng, Trắng, Hồng, Đen}.
b) Xác suất thực nghiệm lấy được con gấu bông màu Hồng là: \(\frac{{10}}{{40}} = \frac{1}{4}\).
Vẽ hình theo yêu cầu đề bài.
a) Sử dụng tính chất của trung điểm để tìm OM, ON.
b) Vì O nằm giữa MN nên MN = OM + ON.

a) Do \(M\) là trung điểm của \(OA\) nên ta có:
\(OM = MA = \frac{{OA}}{2} = \frac{6}{2} = 3(cm)\)
Do \(N\) là trung điểm của \(OB\) nên ta có:
\(ON = NB = \frac{{OB}}{2} = \frac{3}{2} = 1,5(cm)\)
b) Vì điểm \(O\) nằm giữa hai điểm \(M,N\) nên ta có: \(MN = OM + ON\)
Suy ra \(MN = 3 + 1,5 = 4,5(cm)\)
Vậy \({\rm{MN = 4,5 cm}}\).
a) Nhân cả tử và mẫu của các phân số trong A với 2.
Rút 2 ra ngoài, biến đổi các phân số \(\frac{1}{{a\left( {a + 1} \right)}}\) thành \(\frac{1}{a} - \frac{1}{{a + 1}}\) (vì \(\frac{1}{{a\left( {a + 1} \right)}} = \frac{1}{a} - \frac{1}{{a + 1}}\))
Tính A.
b) Để chứng minh phân số tổi giản, ta chứng minh ƯCLN của tử số và mẫu số là 1.
a) Ta có \(A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}} = \frac{2}{6} + \frac{2}{{12}} + \frac{2}{{20}} + \frac{2}{{30}} + ... + \frac{2}{{90}}\)
\(\begin{array}{l} = 2\left( {\frac{1}{{2.3}} + \frac{1}{{3.4}} + \frac{1}{{4.5}} + \frac{1}{{5.6}} + ... + \frac{1}{{9.10}}} \right)\\ = 2\left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + \frac{1}{5} - \frac{1}{6} + ... + \frac{1}{9} - \frac{1}{{10}}} \right)\end{array}\)
\( = 2\left( {\frac{1}{2} - \frac{1}{{10}}} \right) = 2.\frac{4}{{10}} = \frac{4}{5}\).
Vậy \(A = \frac{4}{5}.\)
b) Gọi ƯCLN\(\left( {n - 1\,;\,n - 2} \right) = d\) suy ra \(n - 1 \vdots d\,\,\,,\,\,n - 2 \vdots d\)
suy ra \(\left( {n - 1} \right) - \left( {n - 2} \right) \vdots d\)suy ra \(1 \vdots d \Rightarrow d = 1\) với mọi \(n\)
Vậy với mọi \(n \in {\rm Z}\) thì \(M = \frac{{n - 1}}{{n - 2}}\) là phân số tối giản.