Đề thi giữa kì 2 Toán 6 Cánh diều - Đề số 8 — Không quảng cáo

Dựa vào khái niệm về phân số.

\(\frac{1}{7};\frac{{ - 5}}{3};\frac{0}{{ - 3}}\) là phân số vì có tử số, mẫu số là số nguyên và mẫu số khác 0.

\(\frac{7}{{1,5}}\) không phải phân số vì \(1,5 \notin \mathbb{Z}\).

Đáp án C.

Nghịch đảo của phân số \(\frac{a}{b}\) là \(\frac{b}{a}\) \(\left( {\frac{a}{b}.\frac{b}{a} = 1} \right)\).

Phân số nghịch đảo của phân số \(\frac{{ - 7}}{3}\) là \(\frac{{ - 3}}{7}\) .

Đáp án A.

Hai phân số \(\frac{a}{b} = \frac{c}{d}\) nếu \(ad = bc\).

Hai phân số \(\frac{a}{b} = \frac{c}{d}\) khi \(a.d = b.c\).

Đáp án B.

Dựa vào cách so sánh hai phân số.

\( - 5 >  - 14\) nên \(\frac{{ - 5}}{{11}} > \frac{{ - 14}}{{11}}\) nên A sai.

\(\frac{{ - 5}}{3} < 0\) nên B đúng.

\(13 < 15\) nên \(\frac{2}{{13}} > \frac{2}{{15}}\) nên C sai.

\( - 5 < 8\) nên \(\frac{{ - 5}}{{21}} < \frac{8}{{21}}\) nên D sai.

Đáp án B.

Dựa vào quy tắc cộng hai phân số khác mẫu số.

\(\frac{{ - 12}}{{15}} + \frac{7}{5} = \frac{{ - 12}}{{15}} + \frac{{21}}{{15}} = \frac{9}{{15}} = \frac{3}{5}\).

Đáp án B.

Dựa vào các năm sinh được liệt kê để xác định năm chưa hợp lí.

Năm 2050 chưa xảy ra nên An liệt kê năm sinh của một thành viên là năm 2050 không hợp lý.

Đáp án A.

Khi tung đồng xu một lần có hai kết quả có thể xảy ra với mặt xuất hiện của đồng xu, đó là: mặt S; mặt N.

Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu là: \(\left\{ {S;N} \right\}\).

Đáp án B.

Dựa vào công thức tính xác suất.

Xác suất để thẻ được lấy ghi số 6 là \(\frac{1}{{30}}\).

Đáp án A.

Quan sát hình vẽ để trả lời

Quan sát hình vẽ ta thấy A, B thuộc đường thẳng d và C không thuộc đường thẳng d nên A đúng.

Do đó A, B, C không thẳng hàng và AB không đi qua điểm C.

Đáp án A.

Dựa vào kiến thức về ba điểm thẳng hàng.

Nếu ba điểm cùng thuộc một đường thẳng thì ba điểm đó thẳng hàng nên C đúng.

Đáp án C.

Dựa vào kiến thức về điểm.

J nằm giữa K và L nhưng không nằm chính giữa nên A sai.

Ngoài điểm L còn có điểm J nằm giữa hai điểm K và N nên B sai.

Quan sát hình vẽ ta thấy hai điểm L và N nằm cùng phía so với điểm K nên C đúng.

Khẳng định D sai.

Đáp án C.

Dựa vào kiến thức về điểm thuộc đoạn thẳng.

Vì M thuộc đoạn AB nên AB = AM + MB

Suy ra AM = AB – MB = 6 – 5 = 1(cm)

Đáp án A.

Dựa vào quy tắc tính với phân số.

a) \(\frac{{ - 4}}{7} + \frac{{ - 3}}{7} = \frac{{ - 7}}{7} = - 1\)

b)\(\frac{3}{5} + \frac{{ - 4}}{9}\) \( = \frac{{27}}{{45}} + \frac{{ - 20}}{{45}} = \frac{7}{{45}}\)

c) \(\frac{3}{5} + \frac{2}{5}.\frac{{15}}{8}\)\( = \frac{3}{5} + \frac{3}{4} = \frac{{12}}{{20}} + \frac{{15}}{{20}} = \frac{{27}}{{20}}\)

d) \(\frac{7}{2}.\frac{8}{{13}} + \frac{8}{{13}}.\frac{{ - 5}}{2} + \frac{8}{{13}}\)\( = \frac{8}{{13}}.\left( {\frac{7}{2} + \frac{{ - 5}}{2} + 1} \right) = \frac{8}{{13}}.2 = \frac{{16}}{{13}}\)

Dựa vào quy tắc tính với phân số.

a) \(x + \frac{{11}}{{12}} = \frac{{23}}{{24}}\)

\(\begin{array}{l}x = \frac{{23}}{{24}} - \frac{{11}}{{12}}\\x = \frac{{23}}{{24}} - \frac{{22}}{{24}}\\x = \frac{1}{{24}}\end{array}\)

Vậy \(x = \frac{1}{{24}}\)

b) \(\frac{{11}}{8} - \frac{3}{8} \cdot x = \frac{1}{8}\)

\(\begin{array}{l}\frac{{11}}{8} - \frac{3}{8} \cdot x = \frac{1}{8}\\\frac{3}{8}x = \frac{{11}}{8} - \frac{1}{8}\\\frac{3}{8}x = \frac{5}{4}\\x = \frac{5}{4}:\frac{3}{8}\\x = \frac{{10}}{3}\end{array}\)

Vậy \(x = \frac{{10}}{3}\)

c) \({\left( {{\rm{x}} - \frac{1}{2}} \right)^{\rm{2}}}{\rm{ = }}\frac{{\rm{1}}}{4}\)

\(\begin{array}{l}\left[ \begin{array}{l}{\rm{x}} - \frac{1}{2}{\rm{ = }}\frac{{\rm{1}}}{2}\\{\rm{x}} - \frac{1}{2}{\rm{ = }}\frac{{ - 1}}{2}\end{array} \right.\\\left[ \begin{array}{l}x = \frac{{\rm{1}}}{2} + \frac{1}{2}\\x = \frac{{ - 1}}{2} + \frac{1}{2}\end{array} \right.\\\left[ \begin{array}{l}x = 1\\x = 0\end{array} \right.\end{array}\)

Vậy \(x = 1;x = 0\).

1. Quan sát biểu đồ để trả lời câu hỏi.

2. Xác suất thực nghiệm xuất hiện mặt N khi tung đồng xu nhiều lần bằng tỉ số giữa số lần mặt N xuất hiện với tổng số lần tung đồng xu.

1.

a) Ta có biểu đồ:

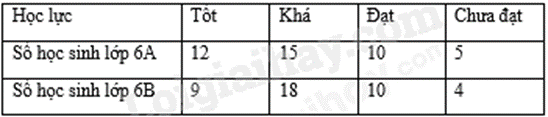
b) Số học sinh lớp 6B là \(9 + 18 + 10 + 4 = 41\)

Số học sinh đạt loại Tốt của lớp 6A nhiều hơn số học sinh đạt loại Tốt của lớp 6B là 12 – 9 = 3 học sinh.

2. Nếu tung đồng xu 22 lần liên tiếp, có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng \(\frac{{13}}{{22}}\).

Vẽ hình theo yêu cầu.

a) Quan sát hình vẽ để xác định điểm nào nằm giữa. Từ đó tính độ dài đoạn thẳng AB theo OA và OB.

b) So sánh OB và BC để xác định.

a) Điểm \(B\) nằm giữa hai điểm \(A\) và \(O\)

Suy ra \(OB + AB = OA\).

Thay \(OA = 5\,cm\); \(OB = 3\,cm\), ta có: \(3 + AB = 5\) suy ra \(AB = 5 - 3\) suy ra \(AB = 2\left( {cm} \right)\)

b) Vì điểm \(A\) nằm giữa hai điểm \(B\) và \(C\) nên \(AB + CA = BC\).

Thay \(CA = {\rm{ }}1\,cm\); \(AB = 2\,cm\),  ta có:  \(2 + {\rm{ }}1{\rm{ }} = {\rm{ }}BC\) suy ra\({\rm{ }}BC = 3\left( {cm} \right)\)

Vì điểm \(B\) nằm giữa hai điểm \(C\) và \(O\) và \(BC = OB = 3\left( {cm} \right)\)

Vậy \(B\)là trung điểm của \(OC\).

Để \(M\) là phân số tối giản thì ƯCLN của \(n - 5\) và \(n - 2\) là 1.

Gọi d là ƯCLN của \(n - 5\) và \(n - 2\).

Khi đó \(\left( {n - 5} \right) \vdots d\)và \(\left( {n - 2} \right) \vdots d\).

Suy ra\(\left[ {n - 5 - \left( {n - 2} \right)} \right] \vdots d\) suy ra \( - 3 \vdots d\).

Mà d = 1 hoặc d = -1  nên M là phân số tối giản thì \(n - 5\) và \(n - 2\) không chia hết cho 3.

Do đó \(n \ne 3k + 5\)và \(n \ne 3k + 2\)

Hay \(n \ne 3k + 2\)\(\left( {k \in \mathbb{Z}} \right)\).