Đề thi học kì 1 Toán 8 - Đề số 3 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Câu 1: Kết quả của phép tính (xy + 5)(xy – 1) là:
Đề bài
Kết quả của phép tính (xy + 5)(xy – 1) là:
-
A.
xy 2 + 4xy – 5 .
-
B.
x 2 y 2 + 4xy – 5 .
-
C.
x 2 – 2xy – 1 .
-
D.
x 2 + 2xy + 5 .
Giá trị của biểu thức \(5{x^2} - \left[ {4{x^2} - 3x\left( {x - 2} \right)} \right]\) tại x = \(\frac{1}{2}\) là:
-
A.
– 3
-
B.
3
-
C.
– 2
-
D.
2
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
a. \({x^3} - 3{x^2} + 3x - 1\)
b. \({x^2} + 8x + 16\)
c. \(3{x^2} + 3x + 1 + {x^3}\)
1. \({\left( {x + 1} \right)^3}\)
2. \({\left( {x - 1} \right)^3}\)
3. \({\left( {x + 4} \right)^2}\)
Hình nào sau đây là hình vuông ?
-
A.
Hình thang cân có một góc vuông.
-
B.
Hình thoi có một góc vuông.
-
C.
Tứ giác có 3 góc vuông.
-
D.
Hình bình hành có một góc vuông.
AM là trung tuyến của tam giác vuông ABC (\(\widehat A = {90^0};M \in BC\)) thì:
-
A.
AC = 2.AM
-
B.
CB = 2.AM
-
C.
BA = 2.AM
-
D.
AM = 2.BC
Hình bình hành ABCD có \(\widehat A = 2\widehat B\). Số đo góc D là:
-
A.
60 0 .
-
B.
120 0 .
-
C.
30 0 .
-
D.
45 0 .
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
-
A.
Hình thang.
-
B.
Hình thang cân.
-
C.
Hình thang vuông.
-
D.
Cả A, B, C đều sai.
M, N là trung điểm các cạnh AB, AC của tam giác ABC. Khi MN = 8cm thì:
-
A.
AB = 16cm
-
B.
AC = 16cm
-
C.
BC = 16cm
-
D.
BC = AB = AC = 16cm
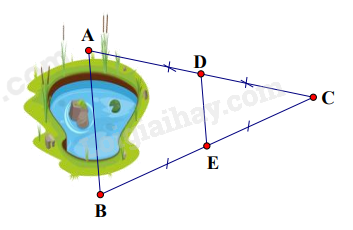
Hai điểm A và B ở hai bờ của một hồ nước (hình vẽ) có độ dài đoạn thẳng DE bằng 100 mét. Hãy xác định khoảng cách AB.
-
A.
200m.
-
B.
100m.
-
C.
150m.
-
D.
50m.
Cho bảng thống kê tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của môi trường đại học về những lớp động vật có xương sống: Cá, Lưỡng cư, Bò sát, Chim, Động vật có vú.

Giá trị chưa hợp lí trong bảng dữ liệu là:
-
A.
Dữ liệu về tên các lớp động vật.
-
B.
Dữ liệu tỉ lệ mẫu vật.
-
C.
A & B đều đúng.
-
D.
A & B đều sai.
Thống kê số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong các năm 2015; 2018; 2019; 2020 . (đơn vi: triệu lượt người)

Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2015 là
-
A.
36,4.
-
B.
53,7.
-
C.
58,5.
-
D.
19,1.
Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2020 là
-
A.
36,4.
-
B.
53,7.
-
C.
58,5
-
D.
19,1.
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong bảng thống kê trên?
-
A.
Biểu đồ tranh.
-
B.
Biểu đồ cột kép.
-
C.
Biểu đồ đoạn thẳng.
-
D.
A; B; C đều sai.
Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022.
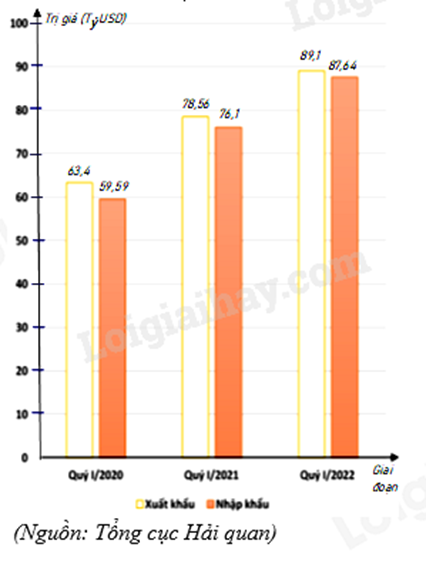
a) Lập bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD) theo mẫu sau:
|
Giai đoạn |
Quý I/2020 |
Quý I/2021 |
Quý I/2022 |
|
Xuất khẩu |
? |
? |
? |
|
Nhập khẩu |
? |
? |
? |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
d) Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm bao nhiêu phần trăm so với quý I năm 2021 (làm tròn kết quả đến hàng phần mười) ?
Lời giải và đáp án
Kết quả của phép tính (xy + 5)(xy – 1) là:
-
A.
xy 2 + 4xy – 5 .
-
B.
x 2 y 2 + 4xy – 5 .
-
C.
x 2 – 2xy – 1 .
-
D.
x 2 + 2xy + 5 .
Đáp án : B
Sử dụng quy tắc nhân hai đa thức.
Ta có:
\(\begin{array}{l}(xy + 5)(xy - 1)\\ = {x^2}{y^2} + 5xy - xy - 5\\ = {x^2}{y^2} + 4xy - 5\end{array}\)
Giá trị của biểu thức \(5{x^2} - \left[ {4{x^2} - 3x\left( {x - 2} \right)} \right]\) tại x = \(\frac{1}{2}\) là:
-
A.
– 3
-
B.
3
-
C.
– 2
-
D.
2
Đáp án : C
Rút gọn biểu thức.
Thay x = \(\frac{1}{2}\) vào biểu thức để tính giá trị.
Ta có:
\(\begin{array}{l}5{x^2} - \left[ {4{x^2} - 3x\left( {x - 2} \right)} \right]\\ = 5{x^2} - \left( {4{x^2} - 3{x^2} + 6x} \right)\\ = 5{x^2} - 4{x^2} + 3{x^2} - 6x\\ = 4{x^2} - 6x\end{array}\)
Thay x = \(\frac{1}{2}\) vào biểu thức, ta được:\(4{\left( {\frac{1}{2}} \right)^2} - 6.\left( {\frac{1}{2}} \right) = 1 - 3 = - 2\).
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
a. \({x^3} - 3{x^2} + 3x - 1\)
b. \({x^2} + 8x + 16\)
c. \(3{x^2} + 3x + 1 + {x^3}\)
1. \({\left( {x + 1} \right)^3}\)
2. \({\left( {x - 1} \right)^3}\)
3. \({\left( {x + 4} \right)^2}\)
a. \({x^3} - 3{x^2} + 3x - 1\)
2. \({\left( {x - 1} \right)^3}\)
b. \({x^2} + 8x + 16\)
3. \({\left( {x + 4} \right)^2}\)
c. \(3{x^2} + 3x + 1 + {x^3}\)
1. \({\left( {x + 1} \right)^3}\)
Sử dụng kiến thức về các hằng đẳng thức đáng nhớ.
a. \({x^3} - 3{x^2} + 3x - 1 = {\left( {x - 1} \right)^3} \Rightarrow \) a – 2.
b. \({x^2} + 8x + 16 = {x^2} + 2.x.4 + {4^2} = {\left( {x + 4} \right)^2} \Rightarrow \) b – 3.
c. \(3{x^2} + 3x + 1 + {x^3} = {x^3} + 3{x^2} + 3x + 1 = {\left( {x + 1} \right)^3} \Rightarrow \) c – 1.
Hình nào sau đây là hình vuông ?
-
A.
Hình thang cân có một góc vuông.
-
B.
Hình thoi có một góc vuông.
-
C.
Tứ giác có 3 góc vuông.
-
D.
Hình bình hành có một góc vuông.
Đáp án : B
Sử dụng dấu hiệu nhận biết hình vuông.
Hình thang cân có một góc vuông là hình chữ nhật nên A sai .
Hình thoi có một góc vuông là hình vuông nên B đúng .
Tứ giác có 3 góc vuông là hình chữ nhật nên C sai .
Hình bình hành có một góc vuông là hình chữ nhật nên D sai .
AM là trung tuyến của tam giác vuông ABC (\(\widehat A = {90^0};M \in BC\)) thì:
-
A.
AC = 2.AM
-
B.
CB = 2.AM
-
C.
BA = 2.AM
-
D.
AM = 2.BC
Đáp án : B
Dựa vào kiến thức về đường trung tuyến ứng với cạnh huyền trong tam giác vuông.
Ta có tam giác ABC vuông tại A và AM là đường trung tuyến (\(M \in BC\)) nên AM chính là đường trung tuyến ứng với cạnh huyền của tam giác vuông ABC. Khi đó: AM = \(\frac{1}{2}\)BC hay BC = 2AM.
Hình bình hành ABCD có \(\widehat A = 2\widehat B\). Số đo góc D là:
-
A.
60 0 .
-
B.
120 0 .
-
C.
30 0 .
-
D.
45 0 .
Đáp án : A
Dựa vào đặc điểm của hình bình hành.
vuông.
Ta có: \(\widehat A + \widehat B = {180^0}\) (hai góc kề một cạnh bù nhau). Mà \(\widehat A = 2\widehat B\) nên:
\(\begin{array}{l}2\widehat B + \widehat B = {180^0}\\3\widehat B = {180^0}\\\widehat B = {180^0}:3 = {60^0}\end{array}\)
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?
-
A.
Hình thang.
-
B.
Hình thang cân.
-
C.
Hình thang vuông.
-
D.
Cả A, B, C đều sai.
Đáp án : B
Sử dụng định lí Thales đảo để chứng minh.
Tam giác ABC cân tại A nên AB = AC.
Vì BM = CN; AB = AC nên AB – BM = AC – CN hay AM = AN
Suy ra \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) => MN // BC (định lí Thales đảo).
Khi đó BMNC là hình thang. Mà BM = CN nên BMNC là hình thang cân.
M, N là trung điểm các cạnh AB, AC của tam giác ABC. Khi MN = 8cm thì:
-
A.
AB = 16cm
-
B.
AC = 16cm
-
C.
BC = 16cm
-
D.
BC = AB = AC = 16cm
Đáp án : C
Sử dụng tính chất đường trung bình.
Ta có M, N là trung điểm các cạnh AB, AC của tam giác ABC nên MN là đường trung bình của tam giác ABC, khi đó MN = \(\frac{1}{2}\)BC.
Mà MN = 8cm nên BC = 8.2 = 16 cm.
Hai điểm A và B ở hai bờ của một hồ nước (hình vẽ) có độ dài đoạn thẳng DE bằng 100 mét. Hãy xác định khoảng cách AB.

-
A.
200m.
-
B.
100m.
-
C.
150m.
-
D.
50m.
Đáp án : A
Sử dụng tính chất của đường trung bình trong tam giác.
Theo hình vẽ, ta thấy AD = DC; BE = EC nên D là trung điểm của AC và E là trung điểm của BC. Khi đó DE là đường trung bình của tam giác ABC => DE = \(\frac{1}{2}\)AB.
Mà DE = 100m => AB = 2.100 = 200(m).
Cho bảng thống kê tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của môi trường đại học về những lớp động vật có xương sống: Cá, Lưỡng cư, Bò sát, Chim, Động vật có vú.

Giá trị chưa hợp lí trong bảng dữ liệu là:
-
A.
Dữ liệu về tên các lớp động vật.
-
B.
Dữ liệu tỉ lệ mẫu vật.
-
C.
A & B đều đúng.
-
D.
A & B đều sai.
Đáp án : B
Quan sát bảng thống kê để xác định.
Trong bảng thống kê trên, ta thấy tổng tỉ lệ mẫu vật bằng 15% + 10% + 20% + 25% + 30% = 100% nên dữ liệu về tổng tỉ lệ mẫu vật chưa chính xác. Vậy dữ liệu tỉ lệ mẫu vật chưa hợp lí.
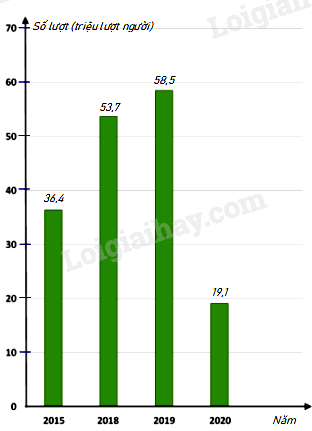
Thống kê số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong các năm 2015; 2018; 2019; 2020 . (đơn vi: triệu lượt người)

Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2015 là
-
A.
36,4.
-
B.
53,7.
-
C.
58,5.
-
D.
19,1.
Đáp án: A
Quan sát bảng thống kê để trả lời câu hỏi.
Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2015 là 36,4 triệu lượt người.
Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2020 là
-
A.
36,4.
-
B.
53,7.
-
C.
58,5
-
D.
19,1.
Đáp án: D
Quan sát bảng thống kê để trả lời câu hỏi.
Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2020 là 19,1 triệu lượt người.
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong bảng thống kê trên?
-
A.
Biểu đồ tranh.
-
B.
Biểu đồ cột kép.
-
C.
Biểu đồ đoạn thẳng.
-
D.
A; B; C đều sai.
Đáp án: D
Quan sát bảng thống kê để trả lời câu hỏi.
Dữ liệu trên nên được biểu diễn bởi biểu đồ cột.
- Rút gọn biểu thức.
- Thay giá trị của x để tính giá trị biểu thức.
a) \(M = {(2x - 1)^2} + 2(2x - 1)(3x + 1) + {(3x + 1)^2}\)
\(\begin{array}{l} = {(2x - 1 + 3x + 1)^2}\\ = {\left( {5x} \right)^2}\\ = 25{x^2}\end{array}\)
Thay \(x = - \frac{1}{5}\) vào M, ta được: \(M = 25.{\left( { - \frac{1}{5}} \right)^2} = 25.\frac{1}{{25}} = 1\).
b) \(N = {(3x - 1)^2} - 2(9{x^2} - 1) + {(3x + 1)^2}\)
\(\begin{array}{l} = {\left( {3x - 1} \right)^2} - 2\left( {3x - 1} \right)\left( {3x + 1} \right) + {\left( {3x + 1} \right)^2}\\ = {\left( {3x - 1 - 3x - 1} \right)^2}\\ = {\left( { - 2} \right)^2}\\ = 4\end{array}\)
Vậy N = 4 với mọi \(x \in \mathbb{R}\).
Sử dụng các phép tính và hằng đẳng thức đáng nhớ.
a) 6x 2 – (2x – 3)(3x + 2) = 1
6x 2 – (6x 2 – 9x + 4x – 6) = 1
6x 2 – 6x 2 + 9x – 4x + 6 = 1
5x + 6 = 1
5x = -5
x = -1
Vậy x = -1.2
b) (x + 1) 3 – (x – 1)(x 2 + x + 1) – 2 = 0
(x 3 + 3x 2 + 3x + 1) – (x 3 – 1) – 2 = 0
x 3 + 3x 2 + 3x + 1 – x 3 + 1 – 2 = 0
3x 2 + 3x = 0
3x(x + 1) = 0
\(\begin{array}{l}\left[ \begin{array}{l}x = 0\\x + 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = - 1\end{array} \right.\end{array}\)
Vậy x = 0 hoặc x = -1.
Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022.

a) Lập bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD) theo mẫu sau:
|
Giai đoạn |
Quý I/2020 |
Quý I/2021 |
Quý I/2022 |
|
Xuất khẩu |
? |
? |
? |
|
Nhập khẩu |
? |
? |
? |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
d) Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm bao nhiêu phần trăm so với quý I năm 2021 (làm tròn kết quả đến hàng phần mười) ?
Dựa vào bảng dữ liệu để trả lời.
a) Bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD)
|
Giai đoạn |
Quý I/2020 |
Quý I/2021 |
Quý I/2022 |
|
Xuất khẩu |
63,4 |
78,56 |
89,1 |
|
Nhập khẩu |
59,59 |
76,1 |
87,64 |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là:
63,4 + 78,56 + 89,1 = 231,06 (tỷ USD)
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là
59,59 + 76,1 + 87,64 = 223,33 (tỷ USD)
d) Tỉ số phần trăm trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 và quý I năm 2021 là: \(\frac{{63,4}}{{78,56}}.100\% = 80,7\% \)
Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm 100 % - 80,7 % = 19,3 % so với quý I năm 2021.
1. Dựa vào tính chất đường phân giác, sử dụng tỉ số bằng nhau để tính.
2.
a) Dựa vào dấu hiệu nhận biết hình bình hành và tính chất đường trung bình để chứng minh.
b) Dựa vào dấu hiệu nhận biết hình thoi và tính chất đường trung bình.
c) Sử dụng tính chất đường trung bình để chứng minh EQ // AB và EN // AB suy ra Q, N, E thẳng hàng.
1.
a)
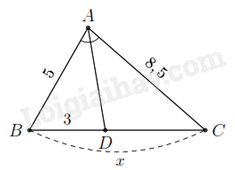
Do \(AD\) là đường phân giác trong của góc \(A\) nên ta có
\(\frac{{DC}}{{DB}} = \frac{{AC}}{{AB}} \Rightarrow DC = \frac{{AC}}{{AB}} \cdot DB.\)
Thay số ta có \(DC = \frac{{8,5}}{5} \cdot 3 = 5,1\). Khi đó \(x = DB + DC = 3 + 5,1 = 8,1\).
b)
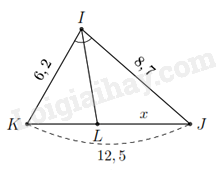
Với \(KL = 12,5 - x\) và do \(IL\) là đường phân giác trong của góc \(I\) nên theo tính chất đường phân giác ta có
Theo tính chất đường phân giác ta có
\(\frac{{KL}}{{LJ}} = \frac{{IK}}{{IJ}} \Rightarrow \frac{{12,5 - x}}{x} = \frac{{6,2}}{{8,7}} \Leftrightarrow x = \frac{{2175}}{{298}} \approx 7,3\).
2.
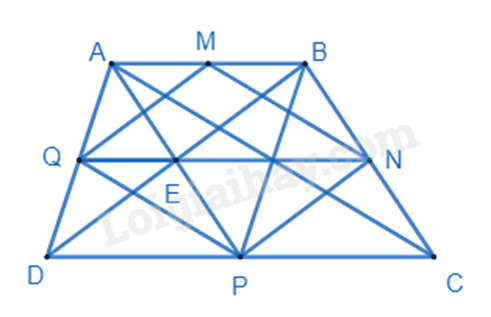
a) Ta có: \(DP = \frac{1}{2}DC = AB\); \(AB//CD \Rightarrow AB//DP\) nên ABPD là hình bình hành.
Vẽ AC, ta có MN là đường trung bình \(\Delta ABC \Rightarrow MN = \frac{1}{2}AC;MN//AC\).
Chứng minh tương tự \( \Rightarrow PQ = \frac{1}{2}AC;PQ//AC\).
\( \Rightarrow MN = PQ;PQ//AC\) nên MNPQ là hình bình hành.
b)
Tương tự như đường chéo AC, vẽ BD, ta cũng chứng minh được MQ và NP là đường trung bình của tam giác ABD và BCD nên \(MQ = NP = \frac{1}{2}BD;MQ//NP//BD\).
MNPQ là hình thoi khi MN = MQ mà \(MN = \frac{1}{2}AC;MQ = \frac{1}{2}BD\) (tính chất đường trung bình)
\( \Rightarrow AC = BD\). Khi đó ABCD là hình thang cân.
c) Vì ABPD là hình bình hành nên E là trung điểm của AP.
Xét tam giác ABD có QE là đường trung bình của tam giác ABD nên QE // AB (1)
Xét tam giác DBC có EN là đường trung bình của tam giác DBC nên EN // DC mà DC // AB nên EN // AB (2)
Từ (1) và (2) suy ra từ E kẻ được EQ // AB và EN // AB nên Q, E, N thẳng hàng