Đề thi học kì 2 Toán 8 - Đề số 1 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Đề bài
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
-
A.
\(1 - {x^2} = 0\).
-
B.
\(2x - 5 = 0\).
-
C.
\(\frac{2}{{x - 3}} + 1 = 0\).
-
D.
\({x^3} - x + 2 = 0\).
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
-
A.
vô nghiệm.
-
B.
vô số nghiệm.
-
C.
có nghiệm duy nhất là \(x = m - 1\).
-
D.
Có 1 nghiệm là \(x = \frac{1}{{m - 1}}\).
Hàm số nào sau đây là hàm số bậc nhất?
-
A.
\(0x + 4 = 0\).
-
B.
\(3{x^2} + 1\).
-
C.
\(y = 2x\).
-
D.
\(y = 0\).
Đường thẳng có hệ số góc bằng 2 và đi qua điểm (1;4) là
-
A.
\(y = 2x + 2\).
-
B.
\(y = 2x - 1\).
-
C.
\(y = - x + 2\).
-
D.
\(y = 2x + 4\).
Giá trị m để đường thẳng \(y = \left( {m + 1} \right)x + 2\) song song với đường thẳng \(y = - 2x\) là:
-
A.
\(m = - 3\).
-
B.
\(m = - 2\).
-
C.
\(m = 2\).
-
D.
\(m = 1\).
Một hộp chứa 16 tấm thẻ cùng loại được đánh số từ 11 đến 26. An lấy ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số chia hết cho 4 là
-
A.
\(\frac{1}{2}\).
-
B.
\(\frac{1}{3}\).
-
C.
\(\frac{1}{4}\).
-
D.
\(\frac{1}{5}\).
Một nhà máy sản xuất laptop tiến hành kiểm tra chất lượng của 500 chiếc laptop được sản xuất và thấy có 6 chiếc bị lỗi. Trong một lô hàng có 1200 chiếc laptop. Hãy dự đoán xem có khoảng bao nhiêu chiếc laptop bị lỗi.
-
A.
12.
-
B.
13.
-
C.
14.
-
D.
15.
-
A.
\(x = 3\).
-
B.
\(x = 4\).
-
C.
\(x = \frac{5}{2}\).
-
D.
\(x = \frac{3}{2}\).
-
A.
\(AB.EC = AC.DC\).
-
B.
\(AB.DE = BC.DC\).
-
C.
\(AC.DE = BC.EC\).
-
D.
\(AB.AC = DE.DC\).
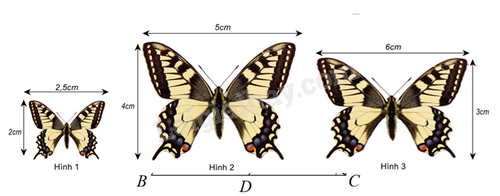
-
A.
Hình 1 và hình 2.
-
B.
Hình 1 và hình 3.
-
C.
Hình 2 và hình 3.
-
D.
Không có hình nào đồng dạng.
Hình chóp tam giác đều có đáy là hình gì?
-
A.
Hình thoi.
-
B.
Hình vuông.
-
C.
Tam giác đều.
-
D.
Tam giác.
Bánh ít có dạng hình chóp tứ giác đều cạnh 3cm, chiều cao 3cm. Thể tích của một chiếc bánh ít là

-
A.
6.
-
B.
9.
-
C.
12.
-
D.
27.
Lời giải và đáp án
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
-
A.
\(1 - {x^2} = 0\).
-
B.
\(2x - 5 = 0\).
-
C.
\(\frac{2}{{x - 3}} + 1 = 0\).
-
D.
\({x^3} - x + 2 = 0\).
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình \(2x - 5 = 0\) có dạng \(ax + b = 0\) với \(a = 2\) nên ta chọn đáp án B.
Đáp án B.
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
-
A.
vô nghiệm.
-
B.
vô số nghiệm.
-
C.
có nghiệm duy nhất là \(x = m - 1\).
-
D.
Có 1 nghiệm là \(x = \frac{1}{{m - 1}}\).
Đáp án : B
Thay m vào phương trình, đưa phương trình về dạng ax + b = 0 để giải.
Thay \(m = - 1\) vào phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\), ta có:
\(\begin{array}{l}\left[ {2{{\left( { - 1} \right)}^2} - 2} \right]x = - 1 + 1\\\left( {2 - 2} \right)x = 0\end{array}\)
\(0.x = 0\) (luôn đúng).
Vậy phương trình có vô số nghiệm.
Đáp án B.
Hàm số nào sau đây là hàm số bậc nhất?
-
A.
\(0x + 4 = 0\).
-
B.
\(3{x^2} + 1\).
-
C.
\(y = 2x\).
-
D.
\(y = 0\).
Đáp án : C
Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b\), trong đó a, b là các số cho trước và \(a \ne 0\).
Hàm số \(y = 2x\) là hàm số bậc nhất với a = 2 và b = 0.
Đáp án C.
Đường thẳng có hệ số góc bằng 2 và đi qua điểm (1;4) là
-
A.
\(y = 2x + 2\).
-
B.
\(y = 2x - 1\).
-
C.
\(y = - x + 2\).
-
D.
\(y = 2x + 4\).
Đáp án : A
Dựa vào kiến thức về đồ thị của hàm số bậc nhất, hệ số góc để tìm phương trình đường thẳng.
Đường thẳng cần tìm có dạng \(y = ax + b\,\left( {a \ne 0} \right)\).
Vì đường thẳng có hệ số góc bằng 2 suy ra a = 2, ta được \(y = 2x + b\).
Đường thẳng đi qua điểm (1;4) nên \(4 = 2.1 + b\) hay \(b = 2\).
Vậy phương trình đường thẳng cần tìm là \(y = 2x + 2\).
Đáp án A.
Giá trị m để đường thẳng \(y = \left( {m + 1} \right)x + 2\) song song với đường thẳng \(y = - 2x\) là:
-
A.
\(m = - 3\).
-
B.
\(m = - 2\).
-
C.
\(m = 2\).
-
D.
\(m = 1\).
Đáp án : A
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a';b \ne b'\).
Để đường thẳng \(y = \left( {m + 1} \right)x + 2\) song song với đường thẳng \(y = - 2x\) thì:
\(\begin{array}{l}m + 1 = - 2\\m = - 3\end{array}\)
Vậy m = -3 thì đường thẳng \(y = \left( {m + 1} \right)x + 2\) song song với đường thẳng \(y = - 2x\).
Đáp án A.
Một hộp chứa 16 tấm thẻ cùng loại được đánh số từ 11 đến 26. An lấy ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số chia hết cho 4 là
-
A.
\(\frac{1}{2}\).
-
B.
\(\frac{1}{3}\).
-
C.
\(\frac{1}{4}\).
-
D.
\(\frac{1}{5}\).
Đáp án : C
Xác định tổng số kết quả có thể và số kết quả thuận lợi cho biến cố
Tính tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể.
Hộp chứa 16 tấm thẻ nên có 16 kết quả có thể khi lấy ngẫu nhiên một thẻ từ hộp.
Có 4 số chia hết cho 4 từ 11 đến 26, đó là 12, 16, 20, 24. Do đó có 4 kết quả thuận lợi cho biến cố thẻ chọn ra ghi số chia hết cho 4.
Vậy xác suất để thẻ chọn ra ghi số chia hết cho 4 là: \(\frac{4}{{16}} = \frac{1}{4}\).
Đáp án C.
Một nhà máy sản xuất laptop tiến hành kiểm tra chất lượng của 500 chiếc laptop được sản xuất và thấy có 6 chiếc bị lỗi. Trong một lô hàng có 1200 chiếc laptop. Hãy dự đoán xem có khoảng bao nhiêu chiếc laptop bị lỗi.
-
A.
12.
-
B.
13.
-
C.
14.
-
D.
15.
Đáp án : C
Tính xác suất laptop lỗi, từ đó suy ra với 1200 chiếc laptop có khoảng bao nhiêu chiếc laptop lỗi.
Xác suất laptop lỗi là: \(\frac{6}{{500}} = \frac{3}{{250}}\)
Do đó trong lô hàng có 1200 chiếc laptop thì có khoảng \(1200.\frac{3}{{250}} = \frac{{72}}{5} \approx 14\) chiếc bị lỗi.
Đáp án C.
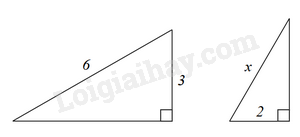
-
A.
\(x = 3\).
-
B.
\(x = 4\).
-
C.
\(x = \frac{5}{2}\).
-
D.
\(x = \frac{3}{2}\).
Đáp án : B
Dựa vào các trường hợp đồng dạng của hai tam giác để tìm x.
Để hai tam giác đồng dạng thì \(\frac{2}{3} = \frac{x}{6}\) suy ra \(x = \frac{2}{3}.6 = 4\).
Đáp án B.
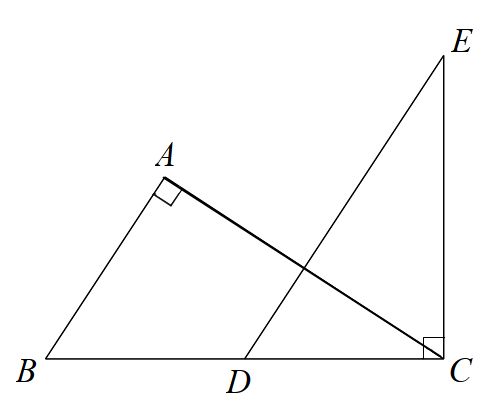
-
A.
\(AB.EC = AC.DC\).
-
B.
\(AB.DE = BC.DC\).
-
C.
\(AC.DE = BC.EC\).
-
D.
\(AB.AC = DE.DC\).
Đáp án : D
Dựa vào AB // DE suy ra \(\widehat {ABC} = \widehat {EDC}\).
Chứng minh $\Delta ABC\backsim \Delta CDE\left( g.g \right)$ suy ra tỉ số giữa các cặp cạnh tương ứng.
Vì AB // DE nên \(\widehat {ABC} = \widehat {EDC}\) (hai góc đồng vị)
Xẻ \(\Delta ABC\) và \(\Delta CDE\) có:
\(\widehat A = \widehat C\left( { = {{90}^0}} \right)\)
\(\widehat {ABC} = \widehat {EDC}\) (cmt)
Suy ra $\Delta ABC\backsim \Delta CDE\left( g.g \right)$. Từ đó ta được:
\(\frac{{AB}}{{AC}} = \frac{{CD}}{{CE}}\) suy ra \(AB.CE = AC.CD\). (A đúng)
\(\frac{{AB}}{{BC}} = \frac{{CD}}{{DE}}\) suy ra \(AB.DE = BC.CD\) (B đúng)
\(\frac{{AC}}{{BC}} = \frac{{CE}}{{DE}}\) suy ra \(AC.DE = CE.BC\) (C đúng)
Vậy D sai (vì không có tỉ lệ nào suy ra \(AB.AC = DE.DC\)).
Đáp án D.
-
A.
Hình 1 và hình 2.
-
B.
Hình 1 và hình 3.
-
C.
Hình 2 và hình 3.
-
D.
Không có hình nào đồng dạng.
Đáp án : A
Kiểm tra tỉ số các cặp cạnh của các hình trên.
Ta có: \(\frac{2}{{2,5}} = \frac{4}{5} \ne \frac{3}{6}\) nên hình 1 và hình 2 là hai hình đồng dạng
Đáp án A.
Hình chóp tam giác đều có đáy là hình gì?
-
A.
Hình thoi.
-
B.
Hình vuông.
-
C.
Tam giác đều.
-
D.
Tam giác.
Đáp án : C
Dựa vào đặc điểm của hình chóp tam giác đều.
Hình chóp tam giác đều có đáy là hình tam giác đều.
Đáp án C.
Bánh ít có dạng hình chóp tứ giác đều cạnh 3cm, chiều cao 3cm. Thể tích của một chiếc bánh ít là

-
A.
6.
-
B.
9.
-
C.
12.
-
D.
27.
Đáp án : B
Dựa vào công thức tính thể tích hình chóp tứ giác: \(V = \frac{1}{3}S.h\) (S là diện tích đáy, h là chiều cao)
Thể tích của một chiếc bánh ít là: \(V = \frac{1}{3}{.3^2}.3 = 9\left( {c{m^3}} \right)\)
Đáp án B.
a) Xác định hai điểm phân biệt thuộc đồ thị hàm số rồi vẽ đường thẳng đi qua hai điểm đó.
b) Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a';b \ne b'\), ta tìm được a.
Thay tọa độ điểm a vào (d”) để tìm b.
a) * Vẽ đường thẳng (d):
Cho x = 1 thì y = -3, đường thẳng (d) đi qua điểm \(A\left( {1; - 3} \right)\).
Cho x = 0 thì y = 0, đường thẳng (d) đi qua gốc tọa độ \(O\left( {0;0} \right)\).
Đường thẳng đi qua hai điểm A, O là đường thẳng (d).
* Vẽ đường thẳng (d’):
Cho x = 0 thì y = 2, đường thẳng (d’) đi qua điểm \(B\left( {0;2} \right)\).
Cho y = 0 thì x = -2, đường thẳng (d’) đi qua điểm \(C\left( { - 2;0} \right)\).
Ta được đồ thị sau:

b) Tìm a, b để đi qua điểm \(A\left( { - 1;3} \right)\) và song song với \(\left( {d'} \right)\).
Vì (d”) song song với (d’) nên \(a = 2;b \ne 2\), hàm số d” có dạng: y = 2x + b.
Vì đồ thị hàm số (d”) đi qua điểm \(A\left( { - 1;3} \right)\) nên thay tọa độ điểm A vào d”, ta được:
\(3 = 2.( - 1) + b\) suy ra \(b = 5\). Ta được: \(y = 2x + 5\)
Vậy a = 2 và b = 5 thì đi qua điểm \(A\left( { - 1;3} \right)\) và song song với \(\left( {d'} \right)\).
Giải bài toán bằng cách lập phương trình.
Gọi quãng đường AB là x (km) (x > 0).
Biểu diễn thời gian xe tải, xe con đi theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi quãng đường AB dài x (km) (x > 0).
Thời gian xe tải đi hết quãng đường AB là \(\frac{x}{{30}}\) (giờ).
\(\frac{3}{4}\) quãng đường AB là \(\frac{3}{4}x\) (km), khi đó thời gian ô tô con đi hết \(\frac{3}{4}\) quãng đường AB là:
\(\frac{3}{4}x:45 = \frac{x}{{60}}\) (giờ)
Vận tốc xe con sau khi tăng thêm 5km/h là:
45 + 5 = 50 (km/h)
Quãng đường còn lại là: \(1 - \frac{3}{4}x = \frac{x}{4}\) (km)
Thời gian xe con đi hết \(\frac{1}{4}\) quãng đường AB là:
\(\frac{x}{4}:50 = \frac{x}{{200}}\) (h)
Vì xe con đến B sớm hơn xe tải là 2 giờ 2 phút = \(\frac{{49}}{{20}}\)h nên ta có phương trình:
\(\begin{array}{l}\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\\\frac{{20x}}{{600}} - \frac{{10x}}{{600}} - \frac{{3x}}{{600}} = \frac{{1470}}{{600}}\\\frac{{7x}}{{600}} = \frac{{1470}}{{600}}\\7x = 1470\\x = 210(TM)\end{array}\)
Vậy quãng đường AB dài 210km.
Sử dụng công thức tính thể tích hình chóp tứ giác đều:
\(V = \frac{1}{3}S.h\) (S là diện tích đáy, h là chiều cao)
Thể tích hình chóp tứ giác giác đều đó là:
\(V = \frac{1}{3}{.40^2}.52 = \frac{{83200}}{3} \approx 27733,3\left( {m{m^3}} \right)\)
a) Chứng minh tam giác MPC và tam giác ABC đồng dạng theo trường hợp góc – góc.
b) Dựa vào tính chất đường phân giác trong tam giác suy ra \(\frac{{BM}}{{MC}} = \frac{{AB}}{{AC}}\).
Cộng cả hai vế với 1 để suy ra \(\frac{{BC}}{{MC}} = \frac{{AB + AC}}{{AC}}\).
c) Kẻ MD vuông góc với AB tại D. Chứng minh \(\Delta MPN = \Delta MBD\left( {ch - gn} \right)\) suy ra \(MP = MB\)
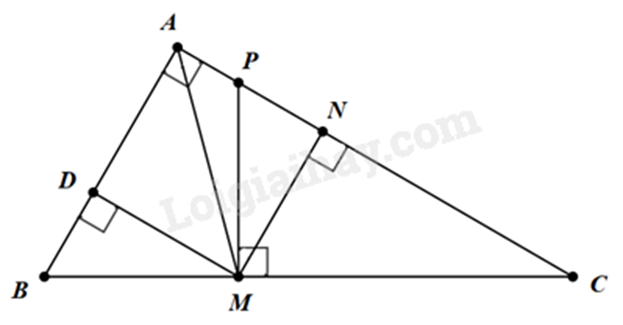
a) Xét \(\Delta MPC\) và \(\Delta ABC\) có:
\(\widehat {PMC} = \widehat {BAC} = {90^0}\)
\(\widehat C\) chung
nên $\Delta MPC\backsim \Delta ABC\left( g.g \right)$ (đpcm)
b) Vì AM là tia phân giác của góc BAC nên \(\frac{{BM}}{{MC}} = \frac{{AB}}{{AC}}\).
Cộng cả hai vế với 1 ta được:
\(\begin{array}{l}\frac{{BM}}{{MC}} + 1 = \frac{{AB}}{{AC}} + 1\\\frac{{BM + MC}}{{MC}} = \frac{{AB + AC}}{{AC}}\\\frac{{BC}}{{MC}} = \frac{{AB + AC}}{{AC}}(dpcm)\end{array}\)
c) Kẻ MD vuông góc với AB tại D.
Xét \(\Delta ADM\) và \(\Delta ANM\) có:
\(\widehat D = \widehat N\left( { = {{90}^0}} \right)\)
\(\widehat {DAM} = \widehat {NAM}\) (AM là tia phân giác của góc BAC)
AM chung
Suy ra \(\Delta ADM = \Delta ANM\) (cạnh huyền – góc nhọn)
Suy ra DM = NM (hai cạnh tương ứng)
Xét \(\Delta MBD\) và \(\Delta MPN\) có:
\(\widehat D = \widehat N\left( { = {{90}^0}} \right)\)
DM = NM (cmt)
\(\widehat {BMD} = \widehat {PMN}\) (cùng phụ với \(\widehat {DMP}\))
Suy ra \(\Delta MBD = \Delta MPN\) (g.c.g)
Suy ra \(MB = MP\) (hai cạnh tương ứng) (đpcm).
Tính xác suất thực nghiệm của biến cố “Lấy được viên bi màu xanh”.
Gọi số bi trong túi là x (x > 9).
Vì số lần thử lớn nên xác suất thực nghiệm gần bằng xác suất của biến cố “Lấy được viên bi màu xanh”.
Do đó ta tính được số viên bi trong hộp, suy ra số viên bi đỏ.
Vì lặp lại phép thử 100 lần, Nam thấy có 40 lần lấy được viên bi đỏ nên số lần lấy được viên bi xanh là:
100 – 40 = 60 (lần).
Do đó xác suất thực nghiệm của biến cố "Lấy được viên bi màu xanh" là:
\(\frac{{60}}{{100}} = \frac{3}{5} = 0.6\)
Gọi số bi trong túi là x (x > 9).
Vì số lần thử lớn nên xác suất thực nghiệm gần bằng xác suất của biến cố “Lấy được viên bi màu xanh”, do đó:
\(\frac{9}{x} \approx 0,6\) suy ra \(x \approx 15\) (viên bi)
Vậy trong hộp có khoảng 15 – 9 = 6 viên bi màu đỏ.