Đề thi học kì 2 Toán 8 - Đề số 2 - Chân trời sáng tạo
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Đề bài
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
-
A.
\(3x - y = 0\).
-
B.
\(2y + 1 = 0\).
-
C.
\(4 + 0.x = 0\).
-
D.
\(3{x^2} = 8\).
Phương trình \(3x + m - x - 1 = 0\) nhận \(x = - 3\) là nghiệm thì m là:
-
A.
\(m = - 3\).
-
B.
\(m = 0\).
-
C.
\(m = 7\).
-
D.
\(m = - 7\)
Một ô tô đi từ A đến B từ 6 giờ sáng, lúc 7 giờ sáng cùng ngày, một xe khách cũng đi từ A và tới B cùng lúc với ô tô. Vậy nếu gọi thời gian đi của xe khách là x ( giờ) thì thời gian đi của ô tô là:
-
A.
\(x + 1\) (giờ).
-
B.
\(x - 1\) (giờ).
-
C.
\(2x\) (giờ).
-
D.
\(x\) (giờ).
Năm nay tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương. Gọi x là tuổi của Phương năm nay vậy thì phương trình tìm x là
-
A.
\(3x + 13 = 2\left( {x + 13} \right)\).
-
B.
\(\frac{x}{3} + 13 = 2\left( {x + 13} \right)\).
-
C.
\(x + 13 = 2\left( {3x + 13} \right)\).
-
D.
\(3x = 2\left( {x + 13} \right)\).
Lớp 8B có 40 học sinh trong đó có 18 học sinh nữ. Lớp phó lao động chọn một bạn để trực nhật trong một buổi học. Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp trong buổi học” là:
-
A.
\(\frac{{11}}{{20}}\).
-
B.
\(\frac{{11}}{9}\).
-
C.
\(\frac{9}{{20}}\).
-
D.
\(\frac{9}{{11}}\).
Một túi đựng các viên kẹo giống hệt nhau, chỉ khác màu nhau, trong đó có 6 viên kẹo màu cam, 3 viên kẹo màu đỏ, 7 viên kẹo màu trắng. An lấy ngẫu nhiên một viên kẹo trong túi. Tính xác suất lấy được viên kẹo màu cam.
-
A.
\(\frac{3}{{16}}\).
-
B.
\(\frac{7}{{16}}\).
-
C.
\(\frac{3}{8}\).
-
D.
\(\frac{9}{{16}}\).
Một cửa hàng thống kê số lượng các loại điện thoại bán được trong một năm vừa qua như sau:

Tính xác suất thực nghiệm của biến cố E: “Chiếc điện thoại loại A được bán năm đó của của hàng”.
-
A.
\(\frac{{143}}{{567}}\).
-
B.
\(\frac{{23}}{{63}}\).
-
C.
\(\frac{{31}}{{81}}\).
-
D.
715.
Cho tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng là 2. Tam giác DEF đồng dạng với tam giác MNP theo tỉ số đồng dạng là 2. Biết \(\widehat A = {30^0}\), tính số đo \(\widehat M\)
-
A.
\(\widehat M = {30^0}\).
-
B.
\(\widehat M = {60^0}\).
-
C.
\(\widehat M = {120^0}\).
-
D.
\(\widehat M = {15^0}\).
Tam ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Biết chu vi tam giác MNP là 12cm, chu vi tam giác ABC là:
-
A.
18cm.
-
B.
24cm.
-
C.
30cm.
-
D.
36cm.
Cho tam giác ABC vuông tại A, đường cao AH. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?
(1) \(A{B^2} = BH.CH\)
(2) \(A{C^2} = CH.BC\)
(3) \(B{C^2} = AB.AC\)
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
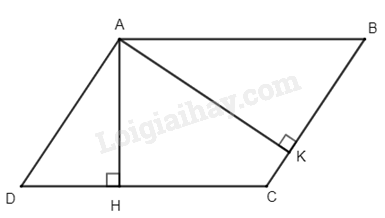
Cho hình bình hành ABCD, kẻ \(AH \bot CD\) tại H; \(AK \bot BC\) tại K. Chọn câu trả lời đúng.
-
A.
\(\Delta HDA\backsim \Delta KAB\).
-
B.
\(\Delta ADH\backsim \Delta AKB\).
-
C.
\(\Delta KAB\backsim \Delta HAD\).
-
D.
\(\Delta BKA\backsim \Delta AHD\).
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Lời giải và đáp án
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
-
A.
\(3x - y = 0\).
-
B.
\(2y + 1 = 0\).
-
C.
\(4 + 0.x = 0\).
-
D.
\(3{x^2} = 8\).
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình \(3x - y = 0\) là phương trình bậc nhất hai ẩn.
Phương trình \(2y + 1 = 0\) là phương trình bậc nhất ẩn y với \(a = 2\) nên ta chọn đáp án B.
Phương trình \(4 + 0.x = 0\) có a = 0 nên không phải phương trình bậc nhất một ẩn.
Phương trình \(3{x^2} = 8\) là phương trình bậc hai.
Đáp án B.
Phương trình \(3x + m - x - 1 = 0\) nhận \(x = - 3\) là nghiệm thì m là:
-
A.
\(m = - 3\).
-
B.
\(m = 0\).
-
C.
\(m = 7\).
-
D.
\(m = - 7\)
Đáp án : C
Thay \(x = - 3\) vào phương trình để tìm m.
Thay \(x = - 3\) vào phương trình \(3x + m - x - 1 = 0\) ta được:
\(\begin{array}{l}3.\left( { - 3} \right) + m - \left( { - 3} \right) - 1 = 0\\ - 9 + m + 3 - 1 = 0\\m - 7 = 0\\m = 7\end{array}\)
Đáp án C.
Một ô tô đi từ A đến B từ 6 giờ sáng, lúc 7 giờ sáng cùng ngày, một xe khách cũng đi từ A và tới B cùng lúc với ô tô. Vậy nếu gọi thời gian đi của xe khách là x ( giờ) thì thời gian đi của ô tô là:
-
A.
\(x + 1\) (giờ).
-
B.
\(x - 1\) (giờ).
-
C.
\(2x\) (giờ).
-
D.
\(x\) (giờ).
Đáp án : A
Biểu diễn thời gian đi của ô tô theo x.
Vì ô tô đi từ A đến B lúc 6 giờ sáng còn xe khách đi từ A đến B lúc 7 giờ sáng và hai xe đến B cùng lúc nên thời gian ô tô đi từ A đến B là x + (7 – 6) = x + 1 (giờ)
Đáp án A.
Năm nay tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương. Gọi x là tuổi của Phương năm nay vậy thì phương trình tìm x là
-
A.
\(3x + 13 = 2\left( {x + 13} \right)\).
-
B.
\(\frac{x}{3} + 13 = 2\left( {x + 13} \right)\).
-
C.
\(x + 13 = 2\left( {3x + 13} \right)\).
-
D.
\(3x = 2\left( {x + 13} \right)\).
Đáp án : A
Biểu diễn các đại lượng qua x.
Tuổi của Phương năm nay là x (tuổi)
Tuổi của mẹ Phương năm nay là 3x (tuổi)
Tuổi của Phương sau 13 năm là x + 13 (tuổi)
Tuổi của mẹ Phương sau 13 năm là 3x + 13 (tuổi)
Vì sau năm tuổi mẹ chỉ còn gấp 2 lần tuổi Phương nên ta có phương trình \(3x + 13 = 2\left( {x + 13} \right)\)
Đáp án A.
Lớp 8B có 40 học sinh trong đó có 18 học sinh nữ. Lớp phó lao động chọn một bạn để trực nhật trong một buổi học. Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp trong buổi học” là:
-
A.
\(\frac{{11}}{{20}}\).
-
B.
\(\frac{{11}}{9}\).
-
C.
\(\frac{9}{{20}}\).
-
D.
\(\frac{9}{{11}}\).
Đáp án : A
Xác định số học sinh nam.
Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp trong buổi học” bằng tỉ số giữa số học sinh nam với tổng số học sinh.
Số học sinh nam của lớp là: \(40 - 18 = 22\) (học sinh)
Xác suất thực nghiệm của biến cố “Một bạn nam trực nhật lớp trong buổi học” là:
\(\frac{{22}}{{40}} = \frac{{11}}{{20}}\)
Đáp án A.
Một túi đựng các viên kẹo giống hệt nhau, chỉ khác màu nhau, trong đó có 6 viên kẹo màu cam, 3 viên kẹo màu đỏ, 7 viên kẹo màu trắng. An lấy ngẫu nhiên một viên kẹo trong túi. Tính xác suất lấy được viên kẹo màu cam.
-
A.
\(\frac{3}{{16}}\).
-
B.
\(\frac{7}{{16}}\).
-
C.
\(\frac{3}{8}\).
-
D.
\(\frac{9}{{16}}\).
Đáp án : C
Xác định tổng số kết quả có thể và số kết quả thuận lợi cho biến cố
Tính tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể.
Có 6 + 3 + 7 = 16 kết quả có thể khi lấy ngẫu nhiên một viên kẹo trong túi.
Có 6 kết quả thuận lợi cho biến cố “lấy được viên kẹo màu cam” nên xác suất lấy được viên kẹo màu cam là:
\(\frac{6}{{16}} = \frac{3}{8}\).
Đáp án C.
Một cửa hàng thống kê số lượng các loại điện thoại bán được trong một năm vừa qua như sau:

Tính xác suất thực nghiệm của biến cố E: “Chiếc điện thoại loại A được bán năm đó của của hàng”.
-
A.
\(\frac{{143}}{{567}}\).
-
B.
\(\frac{{23}}{{63}}\).
-
C.
\(\frac{{31}}{{81}}\).
-
D.
715.
Đáp án : A
Tính tổng số điện thoại bán được trong năm của cửa hàng.
Tính xác suất thực nghiệm của biến cố.
Tổng số điện thoại bán được trong năm của cửa hàng: \(715 + 1035 + 1085 = 2835\) Xác suất thực nghiệm của biến cố E: “Chiếc điện thoại loại A được bán năm đó của của hàng” là:
\(\frac{{715}}{{2835}} = \frac{{143}}{{567}}\)
Đáp án A.
Cho tam giác ABC đồng dạng với tam giác DEF theo tỉ số đồng dạng là 2. Tam giác DEF đồng dạng với tam giác MNP theo tỉ số đồng dạng là 2. Biết \(\widehat A = {30^0}\), tính số đo \(\widehat M\)
-
A.
\(\widehat M = {30^0}\).
-
B.
\(\widehat M = {60^0}\).
-
C.
\(\widehat M = {120^0}\).
-
D.
\(\widehat M = {15^0}\).
Đáp án : A
Chứng minh $\Delta ABC\backsim \Delta MNP$ suy ra số đo góc M.
Vì $\Delta ABC\backsim \Delta DEF$ và $\Delta DEF\backsim \Delta MNP$ suy ra $\Delta ABC\backsim \Delta MNP$ suy ra \(\widehat M = \widehat A = {30^0}\).
Đáp án A.
Tam ABC có M, N, P lần lượt là trung điểm của AB, BC, CA. Biết chu vi tam giác MNP là 12cm, chu vi tam giác ABC là:
-
A.
18cm.
-
B.
24cm.
-
C.
30cm.
-
D.
36cm.
Đáp án : B
Dựa vào hệ số tỉ lệ của hai tam giác để tính chu vi tam giác ABC.
Vì M, N, P lần lượt là trung điểm của AB, BC, CA nên $\Delta ABC\backsim \Delta MNP$ theo hệ số tỉ lệ là 2.
Do đó \({C_{\Delta ABC}} = 2{C_{\Delta MNP}} = 2.12 = 24\left( {cm} \right)\).
Đáp án B.
Cho tam giác ABC vuông tại A, đường cao AH. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?
(1) \(A{B^2} = BH.CH\)
(2) \(A{C^2} = CH.BC\)
(3) \(B{C^2} = AB.AC\)
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Đáp án : B
Xác định các tam giác đồng dạng suy ra tỉ số đồng dạng giữa các cạnh.
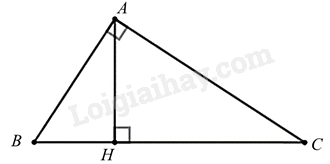
Ta có:
$\Delta ABC\backsim \Delta HBA\left( g.g \right)\Rightarrow \frac{AB}{BC}=\frac{BH}{AB}\Rightarrow A{{B}^{2}}=BH.BC$ nên khẳng định (1) sai.
$\Delta ABC\backsim \Delta HAC\left( g.g \right)\Rightarrow \frac{AC}{BC}=\frac{CH}{AC}\Rightarrow A{{C}^{2}}=CH.BC$ nên khẳng định (2) đúng.
Khẳng định (3) sai.
Vậy chỉ có 1 khẳng định đúng (khẳng định (2)).
Đáp án B.
Cho hình bình hành ABCD, kẻ \(AH \bot CD\) tại H; \(AK \bot BC\) tại K. Chọn câu trả lời đúng.

-
A.
\(\Delta HDA\backsim \Delta KAB\).
-
B.
\(\Delta ADH\backsim \Delta AKB\).
-
C.
\(\Delta KAB\backsim \Delta HAD\).
-
D.
\(\Delta BKA\backsim \Delta AHD\).
Đáp án : C
Dựa vào tính chất của hình bình hành và các trường hợp đồng dạng của hai tam giác vuông để xác định.
Hình bình hành ABCD có \(\widehat B = \widehat D\)
Xét \(\Delta AHD\) và \(\Delta AKB\) có:
\(\widehat H = \widehat K\left( { = {{90}^0}} \right)\)
\(\widehat B = \widehat D\)
suy ra \(\Delta AHD\backsim \Delta AKB\left( gg \right)\)
Các đỉnh tương ứng là: 2 đỉnh A, đỉnh D và đỉnh B, đỉnh H và đỉnh K nên đáp án C đúng.
Đáp án C.
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : A
Xác định đúng các đỉnh của hai hình để nối được tâm phối cảnh của hai hình bên.
Trong các hình trên, chỉ có hình 1 biểu diễn đúng tâm phối cảnh của cặp hình đồng dạng này.

Đáp án A.
a, b) Đưa phương trình về dạng \(ax + b = 0\) để giải.
c, d) Quy đồng bỏ mẫu đưa phương trình về dạng \(ax + b = 0\) để giải.
a) \(x + 2 = - 6x + 16\)
\(\begin{array}{l}x + 6x = 16 - 2\\7x = 14\\x = 2\end{array}\)
Vậy \(x = 2\)
b) \(2\left( {x - 3} \right) = 5\left( {x - 2} \right) + 8\)
\(\begin{array}{l}2x - 6 = 5x - 10 + 8\\2x - 6 = 5x - 2\\2x - 5x = - 2 + 6\\ - 3x = 4\\x = - \frac{4}{3}\end{array}\)
Vậy \(x = - \frac{4}{3}\)
c) \(\frac{{x - 1}}{9} + \frac{{x - 3}}{7} = 2\)
\(\begin{array}{l}\frac{{7\left( {x - 1} \right)}}{{63}} + \frac{{9\left( {x - 3} \right)}}{{63}} = \frac{{2.63}}{{63}}\\7\left( {x - 1} \right) + 9\left( {x - 3} \right) = 2.63\\7x - 7 + 9x - 27 = 126\\7x + 9x = 126 + 27 + 7\\16x = 160\\x = 10\end{array}\)
Vậy \(x = 10\)
d) \(\frac{{2x + 1}}{3} + \frac{{3x - 2}}{2} = \frac{1}{6}\)
\(\begin{array}{l}\frac{{2\left( {2x + 1} \right)}}{6} + \frac{{3\left( {3x - 2} \right)}}{6} = \frac{1}{6}\\2\left( {2x + 1} \right) + 3\left( {3x - 2} \right) = 1\\4x + 2 + 9x - 6 = 1\\13x = 1 + 6 - 2\\13x = 5\\x = \frac{5}{{13}}\end{array}\)
Vậy \(x = \frac{5}{{13}}\)
Giải bài toán bằng cách lập phương trình.
Gọi năng suất dự kiến của tổ sản suất là x (chiếc thảm) (\(x \in N*\)).
Biểu diễn năng suất thực tế và số thảm làm được theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi năng suất của tổ sản suất là x (chiếc thảm) (\(x \in N*\)).
Khi đó năng suất thực tế của tổ là: \(x + 20\% x = 120\% x = 1,2x\)
Số thảm tổ cần dệt là: 20x (chiếc thảm)
Số thảm tổ làm được là: \(18.1,2x = 21,6x\).
Vì tổ còn làm thêm được 24 chiếc thảm so với số thảm được giao nên ta có phương trình:
\(20x + 24 = 21,6x\)
Giải phương trình ta được \(x = 15\)(TM)
Vậy số thảm thực tế tổ sản xuất làm được là: \(21,6.15 = 324\) chiếc thảm.
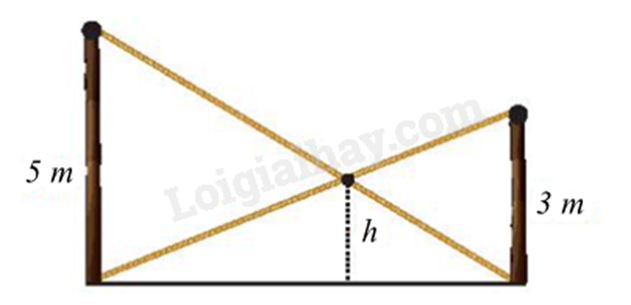
1. - Theo đề bài vẽ lại hình và đặt tên các điểm.
- Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để tính độ cao của h.
2. a) Chứng minh $\Delta ABE\backsim \Delta ACF$ theo trường hợp góc – góc.
b) Chứng minh $\Delta HED\backsim \Delta HCE$ suy ra tỉ số đồng dạng, ta được điều phải chứng minh.
1.
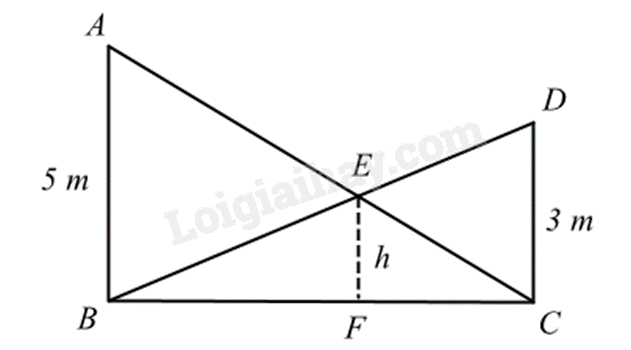
Ta có: AB // CD nên \(\widehat {BAC} = \widehat {DCA}\) và \(\widehat {ABD} = \widehat {CDB}\) (hai góc so le trong)
Xét \(\Delta ABE\) và \(\Delta CDE\) có:
\(\begin{array}{l}\widehat {BAC} = \widehat {DCA}\\\widehat {ABD} = \widehat {CDB}\end{array}\)
Suy ra $\Delta ABE\backsim \Delta CDE$ (gg)
Suy ra \(\frac{{CE}}{{AE}} = \frac{{CD}}{{AB}} = \frac{3}{5}\)
Suy ra \(\frac{{CE}}{{AC}} = \frac{3}{8}\)
Xét \(\Delta CFE\) và \(\Delta CBA\) có:
\(\widehat C\) chung
\(\widehat {ABC} = \widehat {EFC}\)
suy ra $\Delta CFE\backsim \Delta CBA$ (g.g)
suy ra \(\frac{{EF}}{{AB}} = \frac{{CE}}{{AC}} = \frac{3}{8}\). Do đó \(EF = \frac{3}{8}.AB = \frac{3}{8}.5 = \frac{{15}}{8}\) (m)
2.
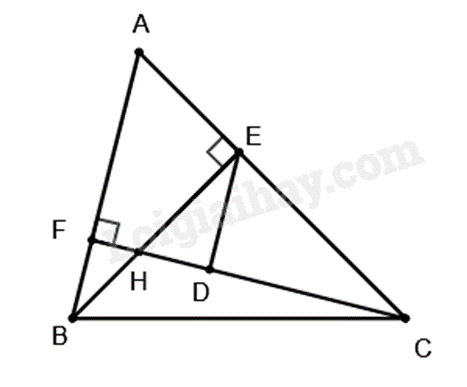
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat {BEA} = \widehat {CFA} = {90^0}\)
\(\widehat A\) chung
suy ra $\Delta ABE\backsim \Delta ACF$ (g.g) (đpcm)
b) Ta có DE // AB nên \(\widehat {HED} = \widehat {ABE}\) (hai góc so le trong)
\(\widehat {ACF} = \widehat {ABE}\) (do $\Delta ABE\backsim \Delta ACF$)
suy ra \(\widehat {ACF} = \widehat {HED}\)
Xét \(\Delta HED\) và \(\Delta HCE\) có:
\(\widehat H\) chung
\(\widehat {ACF} = \widehat {HED}\)
suy ra $\Delta HED\backsim \Delta HCE$ (g.g)
suy ra \(\frac{{HE}}{{HC}} = \frac{{HD}}{{HE}}\) hay \(H{E^2} = HD.HC\) (đpcm)
Số quả trứng có cân nặng dưới 9g = tổng số quả trứng . xác suất một quả trứng cút có cân nặng dưới 9g.
Trong lô 3000 quả trứng cút của trang trại, số quả trứng có cân nặng dưới 9g là:
\(3000.0,5 = 1500\) (quả)
Vậy có khoảng 1500 quả trứng có cân nặng dưới 9g trong lô 3000 quả.
Quy đồng mẫu các phân thức của biểu thức M.
Đặt a – 2 = x, b – 2 = y, c – 2 = z.
Thay vào M ta được \(M = \frac{{{x^3} + {y^3} + {z^3}}}{{xyz}}\).
Từ a + b + c = 6 suy ra x + y + z = 0
Biến đổi để tính M.
Ta có: \(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}\)
\( = \frac{{{{\left( {a - 2} \right)}^3} + {{\left( {b - 2} \right)}^3} + {{\left( {c - 2} \right)}^3}}}{{\left( {a - 2} \right)\left( {b - 2} \right)\left( {c - 2} \right)}}\)
Đặt a – 2 = x, b – 2 = y, c – 2 = z, biểu thức \(M\) trở thành:
\(M = \frac{{{x^3} + {y^3} + {z^3}}}{{xyz}}\)
Mặt khác, từ a + b + c = 6 suy ra \(\left( {a - 2} \right) + \left( {b - 2} \right) + \left( {c - 2} \right) = 0\) hay \(x + y + z = 0\).
Suy ra
\(\begin{array}{l}x + y = - z\\{\left( {x + y} \right)^3} = {\left( { - z} \right)^3}\\{x^3} + {y^3} + 3xy\left( {x + y} \right) = - {z^3}\\{x^3} + {y^3} + 3xy\left( { - z} \right) = - {z^3}\\{x^3} + {y^3} + {z^3} = 3xyz\end{array}\)
Thay vào M ta được:
\(M = \frac{{3xyz}}{{xyz}} = 3\)
Vậy \(M = 3\).