Đề thi học kì 2 Toán 8 - Đề số 4 - Cánh diều
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình bậc nhất một ẩn là
Đề bài
Trong các phương trình sau, phương trình bậc nhất một ẩn là
-
A.
\({x^2} - 1 = 0\).
-
B.
\(3x + 2 = 0\).
-
C.
\(\frac{1}{x} - 3x = 0\).
-
D.
\(\frac{2}{{x - 3}} = 0\).
Nghiệm của phương trình \(4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\) là?
-
A.
\(x = 2\).
-
B.
\(x = \frac{1}{2}\).
-
C.
\(x = 1\).
-
D.
\(x = - 1\).
Phương trình bậc nhất một ẩn \(ax + b = 0\left( {a \ne 0} \right)\). Hạng tử tự do là
-
A.
a.
-
B.
b.
-
C.
0.
-
D.
x.
Phương trình nào dưới đây chỉ có một nghiệm
-
A.
\(4x - 1 = 4x + 3\).
-
B.
\(5 + 2x = 2x - 5\).
-
C.
\(3x - 2x = 3x + 1\).
-
D.
\(x - 7x = 1 - 6x\).
Gọi \(x\) (km) là chiều dài quãng đường AB. Một xe máy đi từ A đến B với vận tốc 40 km/h và đi từ B về A với vận tốc 50 km/h. Biểu thức biểu thị tổng thời gian xe máy đi từ A đến B và từ B về A là
-
A.
\(\frac{x}{{40}} + \frac{x}{{50}}\).
-
B.
\(\frac{x}{{40}} - \frac{x}{{50}}\).
-
C.
\(\frac{x}{{40}}\).
-
D.
\(\frac{x}{{50}}\).
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu:
-
A.
Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
-
B.
Có hai cặp cạnh tương ứng bằng nhau.
-
C.
Hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh bằng nhau.
-
D.
Hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
Cho $\Delta ABC\backsim \Delta A'B'C'$. Khẳng định nào sau đây là sai?
-
A.
\(\frac{{AB}}{{A'B'}} = \frac{{A'C'}}{{AC}} = \frac{{BC}}{{B'C'}}\).
-
B.
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
-
C.
\(\frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{{A'B'}}{{AB}}\).
-
D.
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\).
Điều kiện để $\Delta ABC\backsim \Delta DEF$ theo trường hợp cạnh – góc – cạnh nếu \(\widehat B = \widehat E\) là:
-
A.
\(\frac{{AB}}{{AC}} = \frac{{DE}}{{EF}}\).
-
B.
\(\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}}\).
-
C.
\(\frac{{AB}}{{EF}} = \frac{{BC}}{{DE}}\).
-
D.
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}}\).
-
A.
$\Delta DEF\backsim \Delta HIK$.
-
B.
$\Delta DEF\backsim \Delta MNP$.
-
C.
$\Delta HIK\backsim \Delta MNP$.
-
D.
Cả 3 tam giác đồng dạng.
-
A.
6,4.
-
B.
3,6.
-
C.
17,7.
-
D.
5,6.
Trong các hình sau, cặp hình nào không phải luôn đồng dạng?
-
A.
Tam giác cân.
-
B.
Hình tròn.
-
C.
Tam giác đều.
-
D.
Hình vuông.
-
A.
\(k = \frac{1}{2}\).
-
B.
\(k = 1\).
-
C.
\(k = 2\).
-
D.
\(k = 4\).
Lời giải và đáp án
Trong các phương trình sau, phương trình bậc nhất một ẩn là
-
A.
\({x^2} - 1 = 0\).
-
B.
\(3x + 2 = 0\).
-
C.
\(\frac{1}{x} - 3x = 0\).
-
D.
\(\frac{2}{{x - 3}} = 0\).
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình bậc nhất một ẩn là phương trình \(3x + 2 = 0\).
Đáp án B.
Nghiệm của phương trình \(4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\) là?
-
A.
\(x = 2\).
-
B.
\(x = \frac{1}{2}\).
-
C.
\(x = 1\).
-
D.
\(x = - 1\).
Đáp án : B
Đưa phương trình về dạng \(ax + b = 0\) để giải.
\(\begin{array}{l}4\left( {x - 1} \right) - \left( {x - 2} \right) = - x\\4x - 4 - x + 2 = - x\\3x - 2 = - x\\3x + x = 2\\4x = 2\\x = \frac{1}{2}\end{array}\)
Vậy \(x = \frac{1}{2}\)
Đáp án B.
Phương trình bậc nhất một ẩn \(ax + b = 0\left( {a \ne 0} \right)\). Hạng tử tự do là
-
A.
a.
-
B.
b.
-
C.
0.
-
D.
x.
Đáp án : B
Dựa vào kiến thức về phương trình bậc nhất một ẩn.
Phương trình bậc nhất một ẩn \(ax + b = 0\left( {a \ne 0} \right)\) có hạng tử tự do là b.
Đáp án B.
Phương trình nào dưới đây chỉ có một nghiệm
-
A.
\(4x - 1 = 4x + 3\).
-
B.
\(5 + 2x = 2x - 5\).
-
C.
\(3x - 2x = 3x + 1\).
-
D.
\(x - 7x = 1 - 6x\).
Đáp án : C
Đưa phương trình về dạng ax + b = 0 để giải phương trình.
Ta có:
\(\begin{array}{l}4x - 1 = 4x + 3\\4x - 4x = 3 + 1\end{array}\)
\(0x = 4\) (vô lí)
Phương trình \(4x - 1 = 4x + 3\) vô nghiệm
Giải tương tự, ta được:
Phương trình \(5 + 2x = 2x - 5\) vô nghiệm;
Phương trình \(3x - 2x = 3x + 1\) có nghiệm duy nhất là \(x = - \frac{1}{2}\);
Phương trình \(x - 7x = 1 - 6x\) vô nghiệm.
Đáp án C.
Gọi \(x\) (km) là chiều dài quãng đường AB. Một xe máy đi từ A đến B với vận tốc 40 km/h và đi từ B về A với vận tốc 50 km/h. Biểu thức biểu thị tổng thời gian xe máy đi từ A đến B và từ B về A là
-
A.
\(\frac{x}{{40}} + \frac{x}{{50}}\).
-
B.
\(\frac{x}{{40}} - \frac{x}{{50}}\).
-
C.
\(\frac{x}{{40}}\).
-
D.
\(\frac{x}{{50}}\).
Đáp án : A
Biểu thị thời gian đi và về theo x.
Thời gian xe máy đi từ A đến B là: \(\frac{x}{{40}}\) (h)
Thời gian xe máy đi từ B về A là: \(\frac{x}{{50}}\) (h)
Vậy biểu thức biểu thị tổng thời gian xe máy đi từ A đến B và từ B về A là: \(\frac{x}{{40}} + \frac{x}{{50}}\).
Đáp án A.
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu:
-
A.
Ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
-
B.
Có hai cặp cạnh tương ứng bằng nhau.
-
C.
Hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh bằng nhau.
-
D.
Hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
Đáp án : D
Dựa vào trường hợp đồng dạng góc – góc của hai tam giác.
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
Đáp án D.
Cho $\Delta ABC\backsim \Delta A'B'C'$. Khẳng định nào sau đây là sai?
-
A.
\(\frac{{AB}}{{A'B'}} = \frac{{A'C'}}{{AC}} = \frac{{BC}}{{B'C'}}\).
-
B.
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\).
-
C.
\(\frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{{A'B'}}{{AB}}\).
-
D.
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\).
Đáp án : A
Dựa vào tính chất của hai tam giác đồng dạng.
Vì $\Delta ABC\backsim \Delta A'B'C'$ nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}}\) hay \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\) suy ra B, C, D đúng.
Đáp án A.
Điều kiện để $\Delta ABC\backsim \Delta DEF$ theo trường hợp cạnh – góc – cạnh nếu \(\widehat B = \widehat E\) là:
-
A.
\(\frac{{AB}}{{AC}} = \frac{{DE}}{{EF}}\).
-
B.
\(\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}}\).
-
C.
\(\frac{{AB}}{{EF}} = \frac{{BC}}{{DE}}\).
-
D.
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}}\).
Đáp án : B
Dựa vào trường hợp đồng dạng cạnh – góc – cạnh.
Để $\Delta ABC\backsim \Delta DEF$ theo trường hợp cạnh – góc – cạnh thì \(\widehat B = \widehat E\) và \(\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}}\).
Đáp án B.
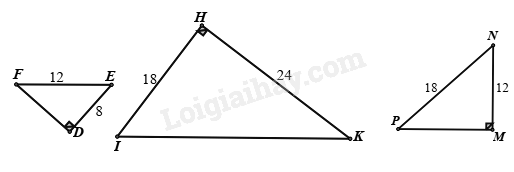
-
A.
$\Delta DEF\backsim \Delta HIK$.
-
B.
$\Delta DEF\backsim \Delta MNP$.
-
C.
$\Delta HIK\backsim \Delta MNP$.
-
D.
Cả 3 tam giác đồng dạng.
Đáp án : B
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
Xét \(\Delta DEF\) và \(\Delta MNP\) có:
\(\begin{array}{l}\widehat D = \widehat M = {90^0}\\\frac{{DE}}{{MN}} = \frac{{EF}}{{NP}}\left( {\frac{8}{{12}} = \frac{{12}}{{18}}\left( { = \frac{2}{3}} \right)} \right)\end{array}\)
nên $\Delta DEF\backsim \Delta MNP$(cạnh huyền – cạnh góc vuông)
Áp dụng định lí Pythagore vào tam giác HIK có:
\(KI = \sqrt {{{18}^2} + {{24}^2}} = 30\)
Vì \(\frac{8}{{12}} = \frac{2}{3} \ne \frac{{18}}{{30}} = \frac{3}{5}\) nên \(\Delta DEF\) không đồng dạng với \(\Delta HIK\).
Điều này dẫn đến \(\Delta MNP\) không đồng dạng với \(\Delta HIK\)(vì $\Delta DEF\backsim \Delta MNP$)
Đáp án B.
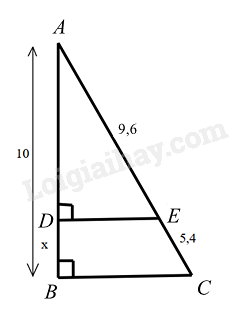
-
A.
6,4.
-
B.
3,6.
-
C.
17,7.
-
D.
5,6.
Đáp án : B
Dựa vào kiến thức về hai tam giác vuông đồng dạng để tìm x.
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(\widehat B = \widehat D = {90^0}\)
\(\widehat A\) chung
Suy ra $\Delta ABC\backsim \Delta ADE$ (g.g)
Do đó \(\frac{{AB}}{{BC}} = \frac{{AD}}{{DE}}\) hay \(\frac{{10}}{{9,6 + 5,4}} = \frac{{AD}}{{9,6}}\)
Suy ra \(AD = 9,6.\frac{{10}}{{9,6 + 5,4}} = 6,4\)
Vậy \(x = AB - AD = 10 - 6,4 = 3,6\).
Đáp án B.
Trong các hình sau, cặp hình nào không phải luôn đồng dạng?
-
A.
Tam giác cân.
-
B.
Hình tròn.
-
C.
Tam giác đều.
-
D.
Hình vuông.
Đáp án : A
Dựa vào đặc điểm của các hình để xác định.
Tam giác cân không phải luôn đồng dạng.
Đáp án A.
-
A.
\(k = \frac{1}{2}\).
-
B.
\(k = 1\).
-
C.
\(k = 2\).
-
D.
\(k = 4\).
Đáp án : A
Dựa vào số đo các cạnh để tìm tỉ số.
Ta có: \(\frac{3}{6} = \frac{4}{8} = \frac{1}{2}\) nên hình ABCD đồng dạng phối cảnh với hình EFGH theo tỉ số đồng dạng là \(k = \frac{1}{2}\) .
Đáp án A.
Đưa phương trình về dạng \(ax + b = 0\) để giải.
a) \(8 + 2\left( {x - 1} \right) = 20\)
\(\begin{array}{l}8 + 2x - 2 = 20\\2x + 6 = 20\\2x = 20 - 6\\2x = 14\\x = 7\end{array}\)
Vậy \(x = 7\)
b) \(4\left( {3x - 2} \right) + 3\left( {x - 4} \right) = 7x + 20\)
\(\begin{array}{l}12x - 8 + 3x - 12 = 7x + 20\\12x + 3x - 7x = 20 + 8 + 12\\8x = 40\\x = 5\end{array}\)
Vậy \(x = 5\)
c) \(\frac{{2x}}{3} + x = \frac{{2x + 5}}{6} + \frac{1}{2}\)
\(\begin{array}{l}\frac{{2.2x}}{6} + \frac{{6x}}{6} = \frac{{2x + 5}}{6} + \frac{3}{6}\\4x + 6x = 2x + 5 + 3\\10x - 2x = 8\\8x = 8\\x = 1\end{array}\)
Vậy \(x = 1\)
Giải bài toán bằng cách lập phương trình.
Gọi số thảm xí nghiệp phải dệt trong 1 ngày theo hợp đồng là x (tấm) (x > 0)
Biểu diễn năng suất mỗi ngày của xí nghiệp, số thảm theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi số thảm xí nghiệp phải dệt trong 1 ngày theo hợp đồng là x (tấm) (x > 0)
Thực tế một ngày xí nghiệp dệt được: x + 7 (tấm)
Số thảm len mà xí nghiệp phải dệt theo hợp đồng là: 17x (tấm)
Thực tế số thảm xí nghiệp dệt được là:
(17 – 2).(x + 7) = 15(x + 7) (tấm)
Theo bài ra ta có phương trình:
\(15(x + 7) = 17x + 7\)
Giải phương trình ta được: \(x = 49\) (thỏa mãn)
Vậy số thảm len xí nghiệp phải dệt theo hợp đồng là: 17.49 = 833 (tấm)
a) Chứng minh $\Delta ABE\backsim \Delta ACF$ theo trường hợp góc – góc suy ra tỉ số các cạnh tương ứng suy ra \(AE.AC = AF.AB\).
b) Chứng minh $\Delta ANB\backsim \Delta ENA$ (g.g) suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra \(A{N^2} = NE.NB\).
c) Dựa vào các tỉ số của câu a và b suy ra \(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\) suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$.
Từ đó suy ra số đo góc AMB.
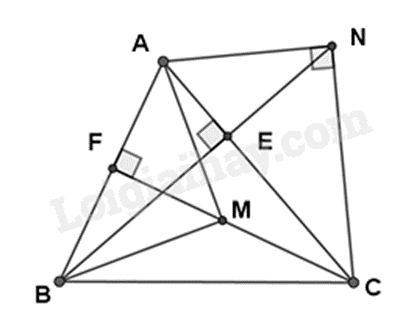
a) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat {AEB} = \widehat {AFC} = {90^0}\)
\(\widehat {BAC}\) chung
Suy ra $\Delta ABE\backsim \Delta ACF$ (g.g). (đpcm)
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\) hay \(AB.AF = AE.AC\)(đpcm) (1)
b) Xét \(\Delta ANE\) và \(\Delta ACN\) có:
\(\widehat {AEN} = \widehat {ANC} = {90^0}\)
\(\widehat {NAC}\) chung
Suy ra $\Delta ANE\backsim \Delta ACN$ (g.g).
Suy ra \(\frac{{AN}}{{AC}} = \frac{{AE}}{{AN}}\) hay \(A{N^2} = AC.AE\) (đpcm). (2)
c) Từ (1) và (2) suy ra \(AB.AF = A{N^2}\).
Mà AM = AN (gt) suy ra \(AM = AB.AF\) hay \(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\).
Xét \(\Delta AMF\) và \(\Delta ABM\) có:
\(\widehat {BAM}\) chung
\(\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}\) (cmt)
Suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$
Suy ra \(\widehat {AMB} = \widehat {AFM} = {90^0}\).
Gọi tuổi thọ của nhà toán học Diphante là x, \(x \in N*\).
Biểu diễn các đại lượng theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi tuổi thọ của nhà toán học Diphante là x (tuổi), \(x \in N*\).
Tuổi niên thiếu của ông là \(\frac{1}{6}x\)
Thời thanh niên của ông là \(\frac{1}{{12}}x\)
Thời vợ chồng chưa có con là: \(\frac{1}{7}x\)
Tuổi của con trai ông là: \(\frac{1}{2}x\)
Theo bài ra ta có phương trình:
\(\frac{1}{6}x + \frac{1}{{12}}x + \frac{1}{7}x + 5 + \frac{1}{2}x + 4 = x\)
Giải phương trình ta được \(x = 84\left( {TM} \right)\)
Vậy tuổi thọ của Diophante là 84 tuổi
Nhân cả hai vế của phương trình với 9, phương trình trở thành \(\left( {3x - 2} \right){\left( {3x + 3} \right)^2}\left( {3x + 8} \right) = - 144\).
Đặt \(3x + 3 = t\), biến đổi phương trình thành \(\left( {t - 5} \right){t^2}\left( {t + 5} \right) = - 144\).
Giải phương trình ta được các giá trị của t.
Thay \(t = 3x + 3\) ta tìm đc x.
Nhân cả hai vế của phương trình \(\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16\) với 9, ta được:
\(\begin{array}{l}9.\left( {3x - 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = - 16.9\\\left( {3x - 2} \right){\left[ {3\left( {x + 1} \right)} \right]^2}\left( {3x + 8} \right) = - 144\\\left( {3x - 2} \right){\left( {3x + 3} \right)^2}\left( {3x + 8} \right) = - 144\end{array}\)
Đặt \(3x + 3 = t\) suy ra \(3x - 2 = t - 5\); \(3x + 8 = t + 5\)
Ta được phương trình biến t như sau:
\(\left( {t - 5} \right){t^2}\left( {t + 5} \right) = - 144\)
\(\begin{array}{l}{t^4} - 25{t^2} + 144 = 0\\\left( {{t^2} - 9} \right)\left( {{t^2} - 16} \right) = 0\\\left[ \begin{array}{l}{t^2} = 9\\{t^2} = 16\end{array} \right.\\\left[ \begin{array}{l}t = \pm 3\\t = \pm 4\end{array} \right.\end{array}\)
Thay \(t = 3x + 3\) ta được:

Vậy nghiệm của phương trình là \(x \in \left\{ {0; - 2;\frac{1}{3};\frac{{ - 7}}{3}} \right\}\).