Đề thi học kì 2 Toán 8 - Đề số 1 - Cánh diều
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Đề bài
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
-
A.
\(1 - {x^2} = 0\).
-
B.
\(2x - 5 = 0\).
-
C.
\(\frac{2}{{x - 3}} + 1 = 0\).
-
D.
\({x^3} - x + 2 = 0\).
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
-
A.
vô nghiệm.
-
B.
vô số nghiệm.
-
C.
có nghiệm duy nhất là \(x = m - 1\).
-
D.
Có 1 nghiệm là \(x = \frac{1}{{m - 1}}\).
Phương trình \(4x - 2 = 0\) có nghiệm là
-
A.
\(x = 2\).
-
B.
\(x = 0\).
-
C.
\(x = - 2\).
-
D.
\(x = \frac{1}{2}\).
Nếu một vòi nước chảy đầy bể trong 5 giờ thì 1 giờ vòi nước đó chảy được bao nhiêu phần bể?
-
A.
\(1\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{1}{5}\).
-
D.
\(5\).
Một tam giác có độ dài các cạnh là \(x + 3\); \(x + 1\); \(x + 5\). Biểu thức biểu thị chu vi tam giác đó là
-
A.
\(3x + 9\)
-
B.
\(x + 9\)
-
C.
\(3x - 9\)
-
D.
\(3x + 16\)
Năm nay chị 27 tuổi và tuổi em ít hơn tuổi chị 5 tuổi. Vậy năm sau tuổi em là
-
A.
21 tuổi
-
B.
22 tuổi
-
C.
23 tuổi
-
D.
24 tuổi
Hãy chọn câu khẳng định đúng.
-
A.
Hai tam giác bằng nhau thì đồng dạng.
-
B.
Hai tam giác đồng dạng thì bằng nhau.
-
C.
Hai tam giác cân luôn đồng dạng.
-
D.
Hai tam giác vuông luôn đồng dạng.
$\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng k. Vậy k bằng tỉ số nào sau đây?
-
A.
\(k = \frac{{AB}}{{BC}}\).
-
B.
\(k = \frac{{AC}}{{DF}}\).
-
C.
\(k = \frac{{DE}}{{AB}}\).
-
D.
\(k = \frac{{DE}}{{DF}}\).
Cho hình sau. Biết \(\Delta ABC,\Delta ADE\) là hai tam giác cân.
Chọn kết luận đúng trong các câu sau:
-
A.
$\Delta ADE\backsim \Delta ABC\left( g.g \right)$ với $k=2$.
-
B.
$\Delta ADE\backsim \Delta ABC\left( c.c.c \right)$ với $k=\frac{2}{3}$.
-
C.
$\Delta ABC\backsim \Delta ADE\left( c.g.c \right)$ với $k=\frac{3}{2}$.
-
D.
$\Delta ABC\backsim \Delta ADE\left( g.g \right)$ với $k=\frac{1}{2}$.
-
A.
\(x = 3\).
-
B.
\(x = 4\).
-
C.
\(x = \frac{5}{2}\).
-
D.
\(x = \frac{3}{2}\).
-
A.
\(AB.EC = AC.DC\).
-
B.
\(AB.DE = BC.DC\).
-
C.
\(AC.DE = BC.EC\).
-
D.
\(AB.AC = DE.DC\).
-
A.
Hình 1 và hình 2.
-
B.
Hình 1 và hình 3.
-
C.
Hình 2 và hình 3.
-
D.
Không có hình nào đồng dạng.
Lời giải và đáp án
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
-
A.
\(1 - {x^2} = 0\).
-
B.
\(2x - 5 = 0\).
-
C.
\(\frac{2}{{x - 3}} + 1 = 0\).
-
D.
\({x^3} - x + 2 = 0\).
Đáp án : B
Phương trình bậc nhất một ẩn có dạng \(ax + b = 0\) với \(a \ne 0\).
Phương trình \(2x - 5 = 0\) có dạng \(ax + b = 0\) với \(a = 2\) nên ta chọn đáp án B.
Đáp án B.
Với \(m = - 1\) thì phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\)
-
A.
vô nghiệm.
-
B.
vô số nghiệm.
-
C.
có nghiệm duy nhất là \(x = m - 1\).
-
D.
Có 1 nghiệm là \(x = \frac{1}{{m - 1}}\).
Đáp án : B
Thay m vào phương trình, đưa phương trình về dạng ax + b = 0 để giải.
Thay \(m = - 1\) vào phương trình \(\left( {2{m^2} - 2} \right)x = m + 1\), ta có:
\(\begin{array}{l}\left[ {2{{\left( { - 1} \right)}^2} - 2} \right]x = - 1 + 1\\\left( {2 - 2} \right)x = 0\end{array}\)
\(0.x = 0\) (luôn đúng).
Vậy phương trình có vô số nghiệm.
Đáp án B.
Phương trình \(4x - 2 = 0\) có nghiệm là
-
A.
\(x = 2\).
-
B.
\(x = 0\).
-
C.
\(x = - 2\).
-
D.
\(x = \frac{1}{2}\).
Đáp án : D
Giải phương trình có dạng \(ax + b = 0\).
Ta có:
\(\begin{array}{l}4x - 2 = 0\\4x = 2\\x = \frac{1}{2}\end{array}\)
Đáp án D.
Nếu một vòi nước chảy đầy bể trong 5 giờ thì 1 giờ vòi nước đó chảy được bao nhiêu phần bể?
-
A.
\(1\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{1}{5}\).
-
D.
\(5\).
Đáp án : C
Coi bể nước bằng 1. Tính số phần bể mà vòi chảy được trong 1 giờ.
Coi bể nước là 1. Vì vòi nước chảy đầy bể trong 5 giờ nên trong 1 giờ vòi chảy được là:
\(1:5 = \frac{1}{5}\) (bể)
Đáp án C.
Một tam giác có độ dài các cạnh là \(x + 3\); \(x + 1\); \(x + 5\). Biểu thức biểu thị chu vi tam giác đó là
-
A.
\(3x + 9\)
-
B.
\(x + 9\)
-
C.
\(3x - 9\)
-
D.
\(3x + 16\)
Đáp án : A
Sử dụng công thức tính chu vi tam giác để viết biểu thức.
Biểu thức biểu thị chu vi tam giác đó là:
\(x + 3 + x + 1 + x + 5 = 3x + 9\).
Đáp án A.
Năm nay chị 27 tuổi và tuổi em ít hơn tuổi chị 5 tuổi. Vậy năm sau tuổi em là
-
A.
21 tuổi
-
B.
22 tuổi
-
C.
23 tuổi
-
D.
24 tuổi
Đáp án : C
Gọi tuổi của em là x, biểu thị tuổi của chị theo tuổi của em và tính tuổi em năm sau.
Gọi tuổi của em là x (tuổi), \(x \in N*\).
Vì tuổi em ít hơn tuổi chị 5 tuổi nên x + 5 = 27
Giải phương trình ta được x = 27 – 5 = 22 (tuổi) (TM)
Vậy năm sau tuổi của em là: 22 + 1 = 23 tuổi.
Đáp án C.
Hãy chọn câu khẳng định đúng.
-
A.
Hai tam giác bằng nhau thì đồng dạng.
-
B.
Hai tam giác đồng dạng thì bằng nhau.
-
C.
Hai tam giác cân luôn đồng dạng.
-
D.
Hai tam giác vuông luôn đồng dạng.
Đáp án : A
Dựa vào kiến thức về hai tam giác đồng dạng.
Hai tam giác bằng nhau thì đồng dạng nên ta chọn đáp án A.
Đáp án A.
$\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng k. Vậy k bằng tỉ số nào sau đây?
-
A.
\(k = \frac{{AB}}{{BC}}\).
-
B.
\(k = \frac{{AC}}{{DF}}\).
-
C.
\(k = \frac{{DE}}{{AB}}\).
-
D.
\(k = \frac{{DE}}{{DF}}\).
Đáp án : B
Xác định tỉ số giữa các cạnh tương ứng của hai tam giác.
$\Delta ABC\backsim \Delta DEF$ nên \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = k\).
Vậy \(k = \frac{{AC}}{{DF}}\).
Đáp án B.
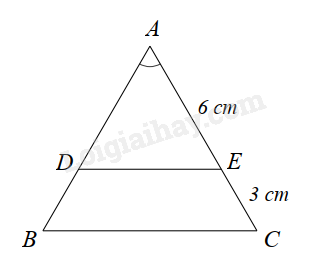
Cho hình sau. Biết \(\Delta ABC,\Delta ADE\) là hai tam giác cân.
Chọn kết luận đúng trong các câu sau:

-
A.
$\Delta ADE\backsim \Delta ABC\left( g.g \right)$ với $k=2$.
-
B.
$\Delta ADE\backsim \Delta ABC\left( c.c.c \right)$ với $k=\frac{2}{3}$.
-
C.
$\Delta ABC\backsim \Delta ADE\left( c.g.c \right)$ với $k=\frac{3}{2}$.
-
D.
$\Delta ABC\backsim \Delta ADE\left( g.g \right)$ với $k=\frac{1}{2}$.
Đáp án : C
Chứng minh $\Delta ADE\backsim \Delta ABC$ theo trường hợp cạnh – góc – cạnh.
Vì \(\Delta ABC,\Delta ADE\) cân nên \(AB = AC\); \(AD = AE\left( { = 6cm} \right)\).
Xét \(\Delta ABC\) và \(\Delta ADE\) có:
\(\widehat A\) chung
\(\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}}\) (vì \(AB = AC;AD = AE\))
suy ra $\Delta ABC\backsim \Delta ADE\left( c.g.c \right)$
suy ra \(k = \frac{{AC}}{{AE}} = \frac{{AE + EC}}{{AE}} = \frac{{6 + 3}}{6} = \frac{9}{6} = \frac{3}{2}\).
Đáp án C.
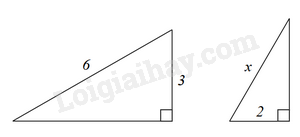
-
A.
\(x = 3\).
-
B.
\(x = 4\).
-
C.
\(x = \frac{5}{2}\).
-
D.
\(x = \frac{3}{2}\).
Đáp án : B
Dựa vào các trường hợp đồng dạng của hai tam giác để tìm x.
Để hai tam giác đồng dạng thì \(\frac{2}{3} = \frac{x}{6}\) suy ra \(x = \frac{2}{3}.6 = 4\).
Đáp án B.
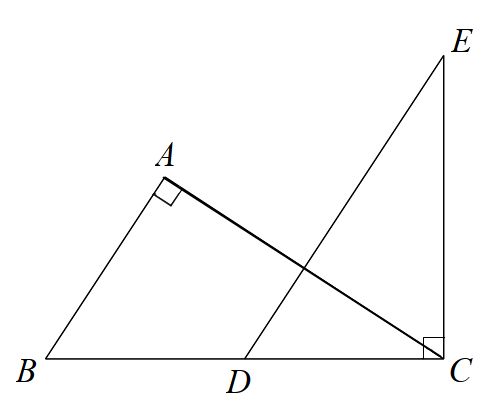
-
A.
\(AB.EC = AC.DC\).
-
B.
\(AB.DE = BC.DC\).
-
C.
\(AC.DE = BC.EC\).
-
D.
\(AB.AC = DE.DC\).
Đáp án : D
Dựa vào AB // DE suy ra \(\widehat {ABC} = \widehat {EDC}\).
Chứng minh $\Delta ABC\backsim \Delta CDE\left( g.g \right)$ suy ra tỉ số giữa các cặp cạnh tương ứng.
Vì AB // DE nên \(\widehat {ABC} = \widehat {EDC}\) (hai góc đồng vị)
Xẻ \(\Delta ABC\) và \(\Delta CDE\) có:
\(\widehat A = \widehat C\left( { = {{90}^0}} \right)\)
\(\widehat {ABC} = \widehat {EDC}\) (cmt)
Suy ra $\Delta ABC\backsim \Delta CDE\left( g.g \right)$. Từ đó ta được:
\(\frac{{AB}}{{AC}} = \frac{{CD}}{{CE}}\) suy ra \(AB.CE = AC.CD\). (A đúng)
\(\frac{{AB}}{{BC}} = \frac{{CD}}{{DE}}\) suy ra \(AB.DE = BC.CD\) (B đúng)
\(\frac{{AC}}{{BC}} = \frac{{CE}}{{DE}}\) suy ra \(AC.DE = CE.BC\) (C đúng)
Vậy D sai (vì không có tỉ lệ nào suy ra \(AB.AC = DE.DC\)).
Đáp án D.
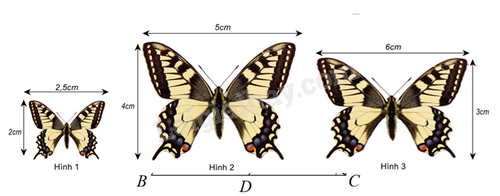
-
A.
Hình 1 và hình 2.
-
B.
Hình 1 và hình 3.
-
C.
Hình 2 và hình 3.
-
D.
Không có hình nào đồng dạng.
Đáp án : A
Kiểm tra tỉ số các cặp cạnh của các hình trên.
Ta có: \(\frac{2}{{2,5}} = \frac{4}{5} \ne \frac{3}{6}\) nên hình 1 và hình 2 là hai hình đồng dạng
Đáp án A.
Đưa phương trình về dạng ax + b = 0 để giải.
a) \(\frac{2}{3}x + 2\frac{1}{2} = 0\)
\(\begin{array}{l}\frac{2}{3}x + \frac{5}{2} = 0\\\frac{2}{3}x = - \frac{5}{2}\\x = - \frac{5}{2}:\frac{2}{3}\\x = - \frac{{15}}{4}\end{array}\)
Vậy nghiệm của phương trình là \(x = - \frac{{15}}{4}\).
b) \(4 - 3x = 5\)
\(\begin{array}{l} - 3x = 5 - 4\\ - 3x = 1\\x = \frac{{ - 1}}{3}\end{array}\)
Vậy nghiệm của phương trình là \(x = \frac{{ - 1}}{3}\).
c) \(\frac{{7x - 1}}{6} = \frac{{16 - x}}{5} - 2x\)
\(\begin{array}{l}\frac{{5\left( {7x - 1} \right)}}{{5.6}} = \frac{{6\left( {16 - x} \right)}}{{6.5}} - \frac{{30.2x}}{{30}}\\5\left( {7x - 1} \right) = 6\left( {16 - x} \right) - 60x\\35x - 5 = 96 - 6x - 60x\\35x + 6x + 60x = 96 + 5\\101x = 101\\x = 1\end{array}\)
Vậy nghiệm của phương trình là \(x = 1\)
Giải bài toán bằng cách lập phương trình.
Gọi quãng đường AB là x (km) (x > 0).
Biểu diễn thời gian xe tải, xe con đi theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi quãng đường AB dài x (km) (x > 0).
Thời gian xe tải đi hết quãng đường AB là \(\frac{x}{{30}}\) (giờ).
\(\frac{3}{4}\) quãng đường AB là \(\frac{3}{4}x\) (km), khi đó thời gian ô tô con đi hết \(\frac{3}{4}\) quãng đường AB là:
\(\frac{3}{4}x:45 = \frac{x}{{60}}\) (giờ)
Vận tốc xe con sau khi tăng thêm 5km/h là:
45 + 5 = 50 (km/h)
Quãng đường còn lại là: \(1 - \frac{3}{4}x = \frac{x}{4}\) (km)
Thời gian xe con đi hết \(\frac{1}{4}\) quãng đường AB là:
\(\frac{x}{4}:50 = \frac{x}{{200}}\) (h)
Vì xe con đến B sớm hơn xe tải là 2 giờ 2 phút = \(\frac{{49}}{{20}}\)h nên ta có phương trình:
\(\begin{array}{l}\frac{x}{{30}} - \left( {\frac{x}{{60}} + \frac{x}{{200}}} \right) = \frac{{49}}{{20}}\\\frac{{20x}}{{600}} - \frac{{10x}}{{600}} - \frac{{3x}}{{600}} = \frac{{1470}}{{600}}\\\frac{{7x}}{{600}} = \frac{{1470}}{{600}}\\7x = 1470\\x = 210(TM)\end{array}\)
Vậy quãng đường AB dài 210km.
Biến đổi tương đương đưa phương trình về dạng ax = b:
+ Nếu a = 0 và b ≠ 0 thì phương trình vô nghiệm.
+ Nếu a ≠ 0 thì phương trình có nghiệm duy nhất \(x = \frac{b}{a}\).
Ta có:
\(2\left( {x - 1} \right) - mx = 3\)
\(\begin{array}{l}2x - 2 - mx = 3\\2x - mx = 3 + 2\\(2 - m)x = 5\end{array}\)
a) Để phương trình \(2\left( {x - 1} \right) - mx = 3\) vô nghiệm thì:
\(2 - m = 0\) suy ra \(m = 2\).
Vậy khi m = 2 thì phương trình vô nghiệm.
b) Để phương trình \(2\left( {x - 1} \right) - mx = 3\) có nghiệm duy nhất thì:
\(2 - m \ne 0\) suy ra \(m \ne 2\).
Vậy khi \(m \ne 2\) thì phương trình có nghiệm duy nhất \(x = \frac{5}{{2 - m}}\).
a) Chứng minh $\Delta AMH\backsim \Delta AHB\left( g.g \right)$
b) Chứng minh $\Delta ANH\backsim \Delta AHC\left( g.g \right)$ suy ra \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) suy ra \(AN.AC = A{H^2}\).
c) Áp dụng định lý Thales để chứng minh \(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\left( { = \frac{{AD}}{{AN}}} \right)\)
Chứng minh $\Delta AFE\backsim \Delta AMH\left( c.g.c \right)$ suy ra \(\widehat {AEF} = \widehat {AHM}\) mà \(\widehat {AHM} = \widehat {ABC}\) nên \(\widehat {AEF} = \widehat {ABC}\).
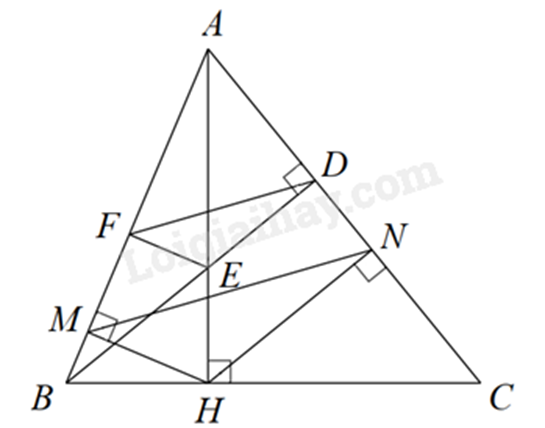
a) Xét \(\Delta AMH\) và \(\Delta AHB\) có:
\(\widehat {AMH} = \widehat {AHB}\left( { = {{90}^0}} \right)\)
\(\widehat A\) chung
suy ra $\Delta AMH\backsim \Delta AHB\left( g.g \right)$ (đpcm)
b) Xét \(\Delta ANH\) và \(\Delta AHC\) có:
\(\widehat {ANH} = \widehat {AHC}\left( { = {{90}^0}} \right)\)
\(\widehat A\) chung
suy ra $\Delta ANH\backsim \Delta AHC\left( g.g \right)$
suy ra \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) suy ra \(AN.AC = A{H^2}\) (đpcm)
c) Vì DF // NM nên \(\frac{{AF}}{{AM}} = \frac{{AD}}{{AN}}\)
Vì DE // HN nên \(\frac{{AE}}{{AH}} = \frac{{AD}}{{AN}}\)
suy ra \(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\)
Xét \(\Delta AFE\) và \(\Delta AMH\) có:
\(\widehat A\) chung
\(\frac{{AF}}{{AM}} = \frac{{AE}}{{AH}}\)
suy ra $\Delta AFE\backsim \Delta AMH\left( c.g.c \right)$ nên \(\widehat {AEF} = \widehat {AHM}\)
Mà \(\widehat {AHM} = \widehat {ABC}\)(vì $\Delta AMH\backsim \Delta AHB$)
Do đó \(\widehat {AEF} = \widehat {ABC}\) (đpcm)
Biến đổi a, b trong phương trình ax = b để tìm x.
Sử dụng kiến thức: \(\frac{1}{{a.b}} = \frac{1}{{b - a}}\left( {\frac{1}{a} - \frac{1}{b}} \right)\) với b > a
Phương trình \(\left( {\frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}} \right)x = \left( {\frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}} \right)\) có dạng ax = b với \(a = \frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}\) và \(b = \frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}\)
Ta có:
\(\begin{array}{l}a = \frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}\\ = \frac{1}{{50}}\left( {\frac{{50}}{{1.51}} + \frac{{50}}{{2.52}} + ... + \frac{{50}}{{10.60}}} \right)\\ = \frac{1}{{50}}\left[ {\left( {1 - \frac{1}{{51}}} \right) + \left( {\frac{1}{2} - \frac{1}{{52}}} \right) + ... + \left( {\frac{1}{{10}} - \frac{1}{{60}}} \right)} \right]\\ = \frac{1}{{50}}\left[ {\left( {1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{10}}} \right) - \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right)} \right]\end{array}\)
\(\begin{array}{l}b = \frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}\\ = \frac{1}{{10}}\left( {\frac{{10}}{{1.11}} + \frac{{10}}{{2.12}} + ... + \frac{{10}}{{50.60}}} \right)\\ = \frac{1}{{10}}\left[ {\left( {1 - \frac{1}{{11}}} \right) + \left( {\frac{1}{2} - \frac{1}{{12}}} \right) + ... + \left( {\frac{1}{{50}} - \frac{1}{{60}}} \right)} \right]\\ = \frac{1}{{10}}\left[ {\left( {1 + \frac{1}{2} + ... + \frac{1}{{50}}} \right) - \left( {\frac{1}{{11}} + \frac{1}{{12}} + ... + \frac{1}{{60}}} \right)} \right]\\ = \frac{1}{{10}}\left[ {\left( {1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{10}}} \right) - \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right)} \right]\\ = 5.\frac{1}{{50}}\left[ {\left( {1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{{10}}} \right) - \left( {\frac{1}{{51}} + \frac{1}{{52}} + ... + \frac{1}{{60}}} \right)} \right]\\ = 5a\end{array}\)
Phương trình trở thành: \(ax = 5a\) suy ra \(x = 5\).
Vậy nghiệm của phương trình \(\left( {\frac{1}{{1.51}} + \frac{1}{{2.52}} + ... + \frac{1}{{10.60}}} \right)x = \left( {\frac{1}{{1.11}} + \frac{1}{{2.12}} + ... + \frac{1}{{50.60}}} \right)\) là \(x = 5\).