Đề thi khảo sát chất lượng đầu năm Toán 6 Cánh diều - Đề số 5
Đề bài
Cho hình vẽ sau:
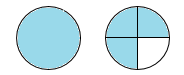
Hỗn số chỉ phần đã tô màu của hình vẽ trên là:
A. $\dfrac{7}{4}$
B. \(2\dfrac{3}{4}\)
C. \(2\dfrac{4}{3}\)
D. \(1\dfrac{3}{4}\)

Tìm một số thập phân biết rằng khi chia số đó cho \(3,25\) rồi cộng với \(24,56\) thì được kết quả là một số tự nhiên lớn nhất có hai chữ số.
A. \(401,57\)
B. \(238,68\)
C. \(2747,25\)
D. \(241,93\)

Điền số thích hợp vào ô trống:

Số thích hợp điền vào chỗ trống thứ nhất (kể từ trái sang phải) là
Số thích hợp điền vào chỗ trống thứ hai (kể từ trái sang phải) là

Điền số thích hợp vào ô trống:
\(38\% \) của \(450\) là
 Tính: \( 293, 75 - 66,26\)
Tính: \( 293, 75 - 66,26\)
A. \( 227,49\)
B. \( 227,19\)
C. \(237,39 \)
D. \(247,49 \)

Điền số thích hợp vào ô trống:
Số thập phân gồm có sáu chục, chín đơn vị, không phần mười, một phần trăm, ba phần nghìn viết là

Phân số \(\dfrac{{27}}{4}\) được viết dưới dạng hỗn số là:
A. \(7\dfrac{2}{4}\)
B. \(6\dfrac{3}{4}\)
C. \(5\dfrac{1}{4}\)
D. \(3\dfrac{6}{4}\)

Viết số thập phân (gọn nhất) thích hợp vào ô trống:
${\rm{176dag}} = $
tạ.

Hỗn số \(5\dfrac{3}{4}\) được viết dưới dạng số thập phân là:
A. \(5,34\)
B. \(5,43\)
C. \(5,375\)
D. \(5,75\)

Điền số thích hợp vào ô trống:
Lúc \(6\) giờ \(30\) phút anh Hai đạp xe từ nhà mình với vận tốc \(12\) km/giờ để đến nhà bạn chơi. Anh đến nhà bạn lúc \(7\) giờ \(10\) phút.
Vậy quãng đường từ nhà anh Hai đến nhà bạn dài
\(km\).

Lan gấp hoa từ \(8\) giờ \(12\) phút đến \(8\) giờ \(40\) phút được \(8\) bông hoa. Hỏi trung bình Lan gấp \(1\) bông hoa trong thời gian bao lâu?
A. \(3,5\) phút
B. \(4,5\) phút
C. \(28\) phút
D. \(40\) phút

Ghép nối hai phép tính có kết quả bằng nhau:
\(3,4:0,1\)
\(34,56:(1,46 + 3,34)\)
\(275,8:100\)
\(7,2 + 12:16\)
\(3:0,25 - 4,05\)
\(18,5 + 155 \times 0,1\)
\(41,37:15\)
\(38,88:5,4\)

Điền số thích hợp vào ô trống:
Một hình chữ nhật có diện tích là \(53,9c{m^2}\), chiều rộng là \(5,5cm\).
Vậy chu vi của hình chữ nhật đó là
\(cm\).

Bác Bình cần làm \(2\) cái thùng hình lập phương bằng sắt không có nắp cạnh $1,8m$ . Hỏi Bác sơn cả bên trong và bên ngoài \(2\) cái thùng đó thì phải mua bao nhiêu ki-lô-gam sơn, biết rằng cứ $20{m^2}$ thì cần $5kg$ sơn.
A. \(32,4kg\)
B. \(16,2kg\)
C. \(8,1kg\)
D. \(4,05kg\)
Tính diện tích phần được tô màu trong hình sau, biết khoảng cách từ tâm \(A\) đến tâm \(B\) là \(1,5cm\):
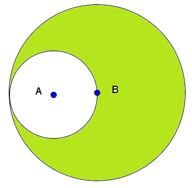
A. \(7,065c{m^2}\)
B. \(21,195c{m^2}\)
C. \(28,26c{m^2}\)
D. \(35,325c{m^2}\)
 Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
A. \(569,5d{m^2}\)
B. \(1139d{m^2}\)
C. \(1394d{m^2}\)
D. \(2278d{m^2}\)

Hai bến sông A và B cách nhau \(40km\). Lúc \(7\) giờ \(20\) phút, một ca nô đi xuôi dòng từ A đến B. Biết vận tốc của ca nô khi đi ngược dòng là \(28\) km/giờ và vận tốc dòng nước là \(2\) km/giờ. Hỏi ca nô đến B lúc mấy giờ?
A. \(8\) giờ \(15\) phút
B. \(8\) giờ \(35\) phút
C. \(8\) giờ \(40\) phút
D. \(8\) giờ \(50\) phút
Lời giải và đáp án
Cho hình vẽ sau:

Hỗn số chỉ phần đã tô màu của hình vẽ trên là:
A. $\dfrac{7}{4}$
B. \(2\dfrac{3}{4}\)
C. \(2\dfrac{4}{3}\)
D. \(1\dfrac{3}{4}\)
D. \(1\dfrac{3}{4}\)
Quan sát hình vẽ, tìm số hình tròn được tô màu và số phần nhỏ của hình tròn được tô màu, từ đó tìm được hỗn số.
Quan sát hình vẽ ta thấy có tất cả \(1\) hình tròn được tô màu toàn bộ, \(1\) hình tròn chia làm \(4\) phần và được tô màu \(3\) phần.
Vậy hỗn số chỉ phần đã tô màu trong hình là \(1\dfrac{3}{4}\).

Tìm một số thập phân biết rằng khi chia số đó cho \(3,25\) rồi cộng với \(24,56\) thì được kết quả là một số tự nhiên lớn nhất có hai chữ số.
A. \(401,57\)
B. \(238,68\)
C. \(2747,25\)
D. \(241,93\)
D. \(241,93\)
Số tự nhiên lớn nhất có hai chữ số là \(99\).
Giả xử \(x\) là số thập phân cần tìm. Theo đề bài ta có \(x:3,25 + 24,56 = 99\). Từ đó ta tìm được \(x\).
Số tự nhiên lớn nhất có hai chữ số là \(99\).
Giả xử \(x\) là số thập phân cần tìm. Theo đề bài ta có \(x:3,25 + 24,56 = 99\).
\(\begin{array}{l}x:3,25 + 24,56 = 99\\x:3,25 = 99 - 24,56\\x:3,25 = 74,44\\x = 74,44 \times 3,25\\x = 241,93\end{array}\)
Vậy số thập phân cần tìm là \(241,93\) .

Điền số thích hợp vào ô trống:

Số thích hợp điền vào chỗ trống thứ nhất (kể từ trái sang phải) là
Số thích hợp điền vào chỗ trống thứ hai (kể từ trái sang phải) là

Số thích hợp điền vào chỗ trống thứ nhất (kể từ trái sang phải) là
Số thích hợp điền vào chỗ trống thứ hai (kể từ trái sang phải) là
Áp dụng công thức: Tích = thừa số × thừa số, sau đó đặt tính rồi tính.
Đặt tính và thực hiện tính ta có:
\(\,\,\,\begin{array}{*{20}{c}}{ \times \begin{array}{*{20}{c}}{6,27}\\{\,\,\,\,\,\,\,8}\end{array}}\\\hline\begin{array}{l}50,16\\\\\end{array}\end{array}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\begin{array}{*{20}{c}}{ \times \begin{array}{*{20}{c}}{2,4\,8}\\{\,\,\,\,1\,4}\end{array}}\\\hline{\,\,9\,\,9\,2}\\{\,\,2\,4\,\,8\,\,\,\,\,\,\,}\\\hline{3\,4,72\,}\end{array}\,\)
Vậy đáp án đúng điền vào ô trống thứ nhất (từ trái sang phải) là $50,16$.
Đáp án đúng điền vào ô trống thứ hai (từ trái sang phải) là $34,72$.

Điền số thích hợp vào ô trống:
\(38\% \) của \(450\) là
\(38\% \) của \(450\) là
Muốn tìm \(38\% \) của \(450\) ta có thể lấy \(450\) chia cho \(100\) rồi nhân với \(38\) hoặc lấy \(450\) nhân với \(38\) rồi chia cho \(100\).
\(38\% \) của \(450\) là: \(450:100 \times 38 = 171\)
Hay \(38\% \) của \(450\) là: \(450 \times 38:100 = 171\)
Vậy đáp án đúng điền vào ô trống là \(171\).
 Tính: \( 293, 75 - 66,26\)
Tính: \( 293, 75 - 66,26\)
A. \( 227,49\)
B. \( 227,19\)
C. \(237,39 \)
D. \(247,49 \)
A. \( 227,49\)
Muốn trừ một số thập phân cho một số thập phân ta làm như sau:
- Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Trừ như trừ các số tự nhiên.
- Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
Ta đặt tính và thực hiện tính như sau:
\( \begin{array}{*{20}{c}}{ - \,\,\begin{array}{*{20}{c}}{293,75}\\{\,\,66,26}\end{array}}\\\hline{\,\,\,\,\,227,49}\end{array}\)
Vậy \(293,75-66,26=227,49\).

Điền số thích hợp vào ô trống:
Số thập phân gồm có sáu chục, chín đơn vị, không phần mười, một phần trăm, ba phần nghìn viết là
Số thập phân gồm có sáu chục, chín đơn vị, không phần mười, một phần trăm, ba phần nghìn viết là
Muốn viết một số thập phân, ta viết lần lượt từ hàng cao đến hàng thấp: trước hết viết phần nguyên, viết dấu “phẩy”, sau đó viết phần thập phân.
Số thập phân gồm có sáu chục, chín đơn vị, không phần mười, một phần trăm, ba phần nghìn viết là \(69,013\).

Phân số \(\dfrac{{27}}{4}\) được viết dưới dạng hỗn số là:
A. \(7\dfrac{2}{4}\)
B. \(6\dfrac{3}{4}\)
C. \(5\dfrac{1}{4}\)
D. \(3\dfrac{6}{4}\)
B. \(6\dfrac{3}{4}\)
- Tính phép chia tử số cho mẫu số
- Giữ nguyên mẫu số của phần phân số
- Tử số bằng số dư của phép chia tử số cho mẫu số
- Phần nguyên bằng thương của phép chia tử số cho mẫu số
Ta có: \(\frac{{27}}{4} = \frac{{24}}{4} + \frac{3}{4} = 6 + \frac{3}{4} = 6\frac{3}{4}\)
Vậy phân số \(\dfrac{{27}}{4}\) được viết dưới dạng hỗn số là \(\dfrac{{27}}{4} = 6\dfrac{3}{4}\)

Viết số thập phân (gọn nhất) thích hợp vào ô trống:
${\rm{176dag}} = $
tạ.
${\rm{176dag}} = $
tạ.
- Xác định hai đơn vị đo khối lượng đã cho (tạ và \(dag\)) và tìm mối liên hệ giữa chúng:
\(1\) tạ \( = 10000dag\) hay \(1dag = \dfrac{1}{{10000}}\) tạ.
- Đổi số đo khối lượng đã cho thành hỗn số có phần phân số là phân số thập phân.
- Đổi hỗn số vừa tìm được thành số thập phân gọn nhất.
Theo bảng đơn vị đo khối lượng ta có \(1\) tạ \( = 10000dag\) hay \(1dag = \dfrac{1}{{10000}}\) tạ.
Nên ${\rm{176dag}} = $\(\dfrac{{176}}{{10000}}\) tạ \( = 0,0176\) tạ.
Vậy ${\rm{176dag}} = 0,0176$ tạ.
Đáp án đúng điền vào ô trống là $0,0176$.

Hỗn số \(5\dfrac{3}{4}\) được viết dưới dạng số thập phân là:
A. \(5,34\)
B. \(5,43\)
C. \(5,375\)
D. \(5,75\)
D. \(5,75\)
- Chuyển hỗn số đã cho thành hỗn số có phần phân số là phân số thập phân bằng cách nhân hoặc chia phần phân số của hỗn số cho \(1\) số thích hợp để mẫu số là $10;{\rm{ }}100;{\rm{ }}1000;...$
- Từ hỗn số mới có phần phân số là phân số thập phân ta viết thành số thập phân.
Ta có: \(5\dfrac{3}{4} = 5\dfrac{{75}}{{100}}\) (nhân cả tử số và mẫu số của phân số \(\dfrac{3}{4}\) với \(25\))
\( = \dfrac{{575}}{{100}} = 5,75\)
Vậy hỗn số \(5\dfrac{3}{4}\) được viết dưới dạng số thập phân là \(5,75\).

Điền số thích hợp vào ô trống:
Lúc \(6\) giờ \(30\) phút anh Hai đạp xe từ nhà mình với vận tốc \(12\) km/giờ để đến nhà bạn chơi. Anh đến nhà bạn lúc \(7\) giờ \(10\) phút.
Vậy quãng đường từ nhà anh Hai đến nhà bạn dài
\(km\).
Lúc \(6\) giờ \(30\) phút anh Hai đạp xe từ nhà mình với vận tốc \(12\) km/giờ để đến nhà bạn chơi. Anh đến nhà bạn lúc \(7\) giờ \(10\) phút.
Vậy quãng đường từ nhà anh Hai đến nhà bạn dài
\(km\).
- Tính thời gian anh Hai đã đi ta lấy thời gian lúc anh Hai tới nhà bạn trừ đi thời gian lúc anh bắt đầu đi.
- Đổi đơn vị đo thời gian sang dạng số thập phần hoặc dạng phân số có đơn vị là giờ.
- Muốn tính quãng đường ta lấy vận tốc nhân với thời gian.
Thời gian anh Hai đi từ nhà đến nhà bạn là:
\(7\) giờ \(10\) phút \( - \,6\) giờ \(30\) phút \( = \,40\) phút
Đổi \(40\) phút \( = \,\dfrac{{40}}{{60}}\) giờ \( = \,\dfrac{2}{3}\) giờ
Quãng đường từ nhà anh Hai đến nhà bạn dài số ki-lô-mét là:
\(12 \times \dfrac{2}{3} = 8 \;(km)\)
Đáp số: \(8km\).
Vậy đáp án đúng điền vào ô trống là \(8\).

Lan gấp hoa từ \(8\) giờ \(12\) phút đến \(8\) giờ \(40\) phút được \(8\) bông hoa. Hỏi trung bình Lan gấp \(1\) bông hoa trong thời gian bao lâu?
A. \(3,5\) phút
B. \(4,5\) phút
C. \(28\) phút
D. \(40\) phút
A. \(3,5\) phút
- Tính thời gian Lan gấp được \(8\) bông hoa, tức là tính \(8\) giờ \(40\) phút \( - \,8\) giờ \(12\) phút.
- Tính thời gian Lan gấp được \(1\) bông hoa ta lấy thời gian Lan gấp được \(8\) bông hoa chia cho \(8\).
Lan gấp được \(8\) bông hoa trong số thời gian là:
\(8\) giờ \(40\) phút \( - \,8\) giờ \(12\) phút \( = \,28\) phút
Lan gấp được \(1\) bông hoa trong số thời gian là:
\(28:8 = 3,5\) (phút)
Đáp số: \(3,5\) phút.

Ghép nối hai phép tính có kết quả bằng nhau:
\(3,4:0,1\)
\(34,56:(1,46 + 3,34)\)
\(275,8:100\)
\(7,2 + 12:16\)
\(3:0,25 - 4,05\)
\(18,5 + 155 \times 0,1\)
\(41,37:15\)
\(38,88:5,4\)
\(3,4:0,1\)
\(18,5 + 155 \times 0,1\)
\(34,56:(1,46 + 3,34)\)
\(38,88:5,4\)
\(275,8:100\)
\(41,37:15\)
\(7,2 + 12:16\)
\(3:0,25 - 4,05\)
- Tính kết quả của từng phép tính rồi tìm hai phép tính có cùng kết quả với nhau.
- Biểu thức có dấu ngoặc thì ta tính trong ngoặc trước, ngoài ngoặc sau.
- Biểu thức có các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau.
Ta có:
+) $3,4:0,1 = 34$
+) \(18,5 + 155 \times 0,1\) $=18,5+15,5$ $=34$
+) \( 3:0,25 - 4,05 =12 - 4,05=7,95\)
+) \(7,2 + 12:16 = 7,2 + 0,75 = 7,95\)
+) \(34,56:(1,46 + 3,34) = 34,56:4,8\) $=7,2$
+) \(38,88:5,4 = 7,2\)
+) \(275,8:100 = 2,758\)
+) \(\,41,37:15 = 2,758\)
Vậy các biểu thức được ghép nối với nhau là:
+) $3,4:0,1$ và \(18,5 + 155 \times 0,1\).
+) \(34,56:(1,46 + 3,34)\) và \(38,88:5,4 \).
+) \(275,8:100\) và \(\,41,37:15 \).
+) \(7,2 + 12:16 \) và \( 3:0,25 - 4,05\).

Điền số thích hợp vào ô trống:
Một hình chữ nhật có diện tích là \(53,9c{m^2}\), chiều rộng là \(5,5cm\).
Vậy chu vi của hình chữ nhật đó là
\(cm\).
Một hình chữ nhật có diện tích là \(53,9c{m^2}\), chiều rộng là \(5,5cm\).
Vậy chu vi của hình chữ nhật đó là
\(cm\).
- Tìm chiều dài hình chữ nhật theo công thức:
Chiều dài = diện tích hình chữ nhật : chiều rộng.
- Tính chu vi hình chữ nhật theo công thức:
Chu vi hình chữ nhật = (Chiều dài + chiều rộng) \( \times 2\).
Chiều dài hình chữ nhật đó là:
\(53,9:5,5 = 9,8\;(cm)\)
Chu vi hình chữ nhật đó là:
\((9,8 + 5,5) \times 2 = 30,6\;(cm)\)
Đáp số: \(30,6cm\).
Vậy đáp án đúng điền vào ô trống là \(30,6\).

Bác Bình cần làm \(2\) cái thùng hình lập phương bằng sắt không có nắp cạnh $1,8m$ . Hỏi Bác sơn cả bên trong và bên ngoài \(2\) cái thùng đó thì phải mua bao nhiêu ki-lô-gam sơn, biết rằng cứ $20{m^2}$ thì cần $5kg$ sơn.
A. \(32,4kg\)
B. \(16,2kg\)
C. \(8,1kg\)
D. \(4,05kg\)
B. \(16,2kg\)
Vì cái thùng đó có dạng là hình lập phương và không có nắp nên cái hộp đó có \(5\) mặt. Diện tích khi sơn bên trong (hoặc bên ngoài) của \(1\) thùng bằng diện tích một mặt nhân với \(5\).
Để giải ta có thể thực hiện các bước như sau:
- Tính diện tích một mặt của cái thùng ta lấy độ dài một cạnh nhân với chính nó.
- Tính diện tích cần sơn khi sơn bên trong của \(1\) cái thùng ta lấy diện tích một mặt nhân với \(5\).
- Tính diện tích cần sơn khi sơn bên trong và bên ngoài của \(1\) cái thùng ta lấy diện tích cần sơn khi sơn bên trong nhân với \(2\).
- Tính khối lượng cần sơn \(1\) cái thùng ta lấy diện tích cần sơn chia cho \(20\) rồi nhân với \(4\) (dạng toán tỉ lệ thuận).
- Tính khối lượng cần sơn \(2\) cái thùng ta lấy khối lượng cần sơn \(1\) cái thùng nhân với \(2\)
nhân với \(2\).
Diện tích một mặt của cái thùng đó là:
$1,8 \times 1,8 = 3,24\;({m^2})$
Diện tích cần sơn khi sơn bên trong của \(1\) cái thùng:
$3,24 \times 5 = 16,2\; ({m^2})$
Diện tích cần sơn khi sơn bên trong và bên ngoài của \(1\) cái thùng là:
$16,2 \times 2 = 32,4\; ({m^2})$
Khối lượng sơn ta cần dùng để sơn \(1\) cái thùng là:
\(32,4:20 \times 5 = 8,1\;(kg)\)
Khối lượng sơn ta cần dùng để sơn \(2\) cái thùng là:
\(8,1 \times 2 = 16,2\;(kg)\)
Đáp số: \(16,2kg\).
Tính diện tích phần được tô màu trong hình sau, biết khoảng cách từ tâm \(A\) đến tâm \(B\) là \(1,5cm\):

A. \(7,065c{m^2}\)
B. \(21,195c{m^2}\)
C. \(28,26c{m^2}\)
D. \(35,325c{m^2}\)
B. \(21,195c{m^2}\)
- Xác định bán kính của hai hình tròn: hình tròn tâm \(A\) có bán kính là \(AB = 1,5cm\) và hình tròn tâm \(B\) có bán kính là \(1,5 \times 2 = 3cm\).
- Tính diện tích của hai hình tròn theo công thức: \(S = r \times r \times 3,14\).
- Tính diện tích phần tô màu ta lấy diện tích hình tròn tâm \(B\) trừ đi diện tích hình tròn tâm \(A\).
Khoảng cách từ tâm \(A\) đến tâm \(B\) là \(1,5cm\) nên ta có \(AB = 1,5cm\).
\(AB\) chính là bán kính của hình tròn tâm \(A\), vậy hình tròn tâm \(A\) có bán kính là \(1,5cm\).
Hình tròn tâm \(B\) có bán kính chính là đường kính của hình tròn tâm \(A\).
Vậy hình tròn tâm \(B\) có bán kính là:
\(1,5 \times 2 = 3 \;(cm)\)
Diện tích của hình tròn tâm \(A\) là:
\(1,5 \times 1,5 \times 3,14 = 7,065\;(c{m^2})\)
Diện tích của hình tròn tâm \(B\) là:
\(3 \times 3 \times 3,14 = 28,26\;(c{m^2})\)
Diện tích của phần được tô màu là:
\(28,26 - 7,065 = 21,195\;(c{m^2})\)
Đáp số: \(21,195c{m^2}\).
 Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
A. \(569,5d{m^2}\)
B. \(1139d{m^2}\)
C. \(1394d{m^2}\)
D. \(2278d{m^2}\)
B. \(1139d{m^2}\)
- Vẽ hình theo đề bài ta thấy diện tích phần tăng thêm là diện tích tam giác \(ACD\) có đáy \(CD = 15cm\) và chiều cao chính là chiều cao \(AH\) của tam giác \(ABC\), từ đó áp dụng công thức \(h = S \times 2:a\) ta tìm được chiều cao \(AH\).
- Tính diện tích tam giác \(ABC\) theo công thức \(S = a \times h:2\).
Theo bài ra ta có hình vẽ

Phần diện tích tăng thêm chính là diện tích của hình tam giác có đáy là $15dm$ và chiều cao cũng chính là chiều cao \(AH\) của tam giác \(ABC\).
Chiều cao của tam giác \(ABC\) là:
\(255 \times 2:15 = 34\;(dm)\)
Diện tích tam giác \(ABC\) là
\(67 \times 34:2 = 1139\left( {d{m^2}} \right)\)
Đáp số: \(1139d{m^2}\).

Hai bến sông A và B cách nhau \(40km\). Lúc \(7\) giờ \(20\) phút, một ca nô đi xuôi dòng từ A đến B. Biết vận tốc của ca nô khi đi ngược dòng là \(28\) km/giờ và vận tốc dòng nước là \(2\) km/giờ. Hỏi ca nô đến B lúc mấy giờ?
A. \(8\) giờ \(15\) phút
B. \(8\) giờ \(35\) phút
C. \(8\) giờ \(40\) phút
D. \(8\) giờ \(50\) phút
B. \(8\) giờ \(35\) phút
- Tính vận tốc của ca nô khi nước yên lặng và vận tốc xuôi dòng theo công thức:
Vận tốc khi nước lặng \(=\) vận tốc ngược dòng \(+\) vận tốc dòng nước;
Vận tốc xuôi dòng \(=\) vận tốc khi nước lặng \(+\) vận tốc dòng nước
- Tính thời gian đi xuôi dòng ta lấy độ dài từ bến A đến bến B chia cho vận tốc đi xuôi dòng.
- Tính thời gian ca nô đến B theo công thức:
Thời gian đến \(=\) thời gian xuất phát \(+\) thời gian đi \(+\) thời gian nghỉ (nếu có).
Vận tốc của ca nô khi nước lặng là:
\(28 + 2 = 30\) (km/giờ)
Vận tốc của ca nô khi đi xuôi dòng là:
\(30 + 2 = 32\) (km/giờ)
Ca nô đi xuôi dòng từ A đến B hết số thời gian là:
\(40:32 = 1,25\) (giờ)
Đổi \(1,25\) giờ \( = \,1\) giờ \(15\) phút
Ca nô đến B lúc:
\(7\) giờ \(20\) phút \( + \,1\) giờ \(15\) phút \( = \,8\) giờ \(35\) phút
Đáp số: \(8\) giờ \(35\) phút.