Đề thi khảo sát chất lượng đầu năm Toán 9- Đề số 1
Đề bài
Phân tích đa thức \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\) thành nhân tử ta được:
-
A.
\(5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
-
B.
\(5{x^2}{y^3}\left( { - 5xy + 2x} \right)\)
-
C.
\({x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
-
D.
\(5{x^2}{y^3}\left( {1 - xy + x} \right)\)
Phương trình \(7x + 4\; = 3x-{\rm{ }}1\) có tập nghiệm là:
-
A.
\(S = \left\{ {\dfrac{{ - 5}}{4}} \right\}\)
-
B.
\(S = \left\{ {\dfrac{5}{4}} \right\}\)
-
C.
\(S = \left\{ { - 1} \right\}\)
-
D.
\(S = \left\{ 0 \right\}\)
Khi \(x \ge 3\), kết quả rút gọn của biểu thức \(2{\rm{x}} + \left| {x - 3} \right| - 1\) là:
-
A.
\(3x + 2\)
-
B.
\(3x - 4\)
-
C.
\(x + 2\)
-
D.
\(4 - 3x\)
Cho \(\Delta MNP \backsim \Delta HGK\) có tỉ số chu vi: \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}.\) Chọn câu đúng.
-
A.
\(\dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)
-
B.
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{2}{7}\)
-
C.
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{{49}}{4}\)
-
D.
\(\dfrac{{NP}}{{GK}} = \dfrac{5}{7}\)
Giá trị \(x = 2\) là nghiệm của bất phương trình nào dưới đây?
-
A.
\(2x + 5 > 11\)
-
B.
\(4-x > 3x-1\)
-
C.
\( - 4{\rm{x}} + 7 > x - 1\)
-
D.
\({x^2} + 3 > 6x-7\)
Rút gọn biểu thức \({\left( {x + y} \right)^2} + {\rm{ }}{\left( {x - y} \right)^2}\), ta được kết quả là:
-
A.
\(2\left( {{x^2} + {\rm{ }}{y^2}} \right)\)
-
B.
\(2{x^2} + {\rm{ }}{y^2}\)
-
C.
\(2\left( {{x^2} - {\rm{ }}{y^2}} \right)\)
-
D.
Một kết quả khác
Phương trình \(\left| {x - 4} \right| + 3x = 5\) có tổng các nghiệm là:
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{{11}}{4}\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(1\)
Phương trình \({x^3} - 9x = 0\) có bao nhiêu nghiệm?
-
A.
\(1\)
-
B.
\(3\)
-
C.
\(4\)
-
D.
\(2\)
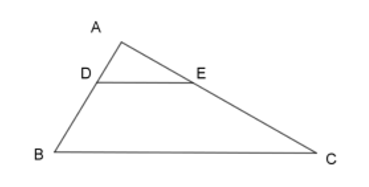
Cho hình vẽ, biết \(DE// BC\). Khẳng định nào sau đây là đúng ?
-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\)
-
B.
\(AD.AE = AB.AC\)
-
C.
\(\dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC}}\)
-
D.
\(DE.AD = AB.BC\)
Diện tích toàn phần của hình lập phương có độ dài cạnh đáy bằng 5cm là:
-
A.
\(25\,c{m^2}\)
-
B.
\(125\,c{m^2}\)
-
C.
\(150\,c{m^2}\)
-
D.
\(250\,c{m^2}\)
Một người đi xe máy từ A đến B với vận tốc trung bình 30km/giờ. Khi đi được 1 giờ thì xe bị hỏng, người đó phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xong người đó đi tiếp tới B, để đến B đúng giờ đã định người đó phải tăng vận tốc thêm 6km/h. Tính độ dài quãng đường AB.
-
A.
\(60\,km\)
-
B.
\(120\,km\)
-
C.
\(90\,km\)
-
D.
\(150\,km\)
Giải phương trình \(\dfrac{{x + 5}}{{x - 5}} - \dfrac{{x - 5}}{{x + 5}} = \dfrac{{20}}{{{x^2} - 25}}\) ta được nghiệm là:
-
A.
\(x = 5\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = -1\)
Cho \(a,b,c > 0\) thỏa mãn: \(6a + 2b + 3c = 11.\) Tìm giá trị nhỏ nhất của biểu thức \(M = \dfrac{{2b + 3c + 16}}{{1 + 6a}} + \dfrac{{6a + 3c + 16}}{{1 + 2b}} + \dfrac{{6a + 2b + 16}}{{1 + 3c}}\).
-
A.
\(8\)
-
B.
\(9\)
-
C.
\(15\)
-
D.
\(11\)
Lời giải và đáp án
Phân tích đa thức \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\) thành nhân tử ta được:
-
A.
\(5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
-
B.
\(5{x^2}{y^3}\left( { - 5xy + 2x} \right)\)
-
C.
\({x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
-
D.
\(5{x^2}{y^3}\left( {1 - xy + x} \right)\)
Đáp án : A
Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.
Ta có: \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\)\( = 5{x^2}{y^3}. 1 - 5{x^2}{y^3}. 5xy + 5{x^2}{y^3}. 2x\)\( = 5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\).
Phương trình \(7x + 4\; = 3x-{\rm{ }}1\) có tập nghiệm là:
-
A.
\(S = \left\{ {\dfrac{{ - 5}}{4}} \right\}\)
-
B.
\(S = \left\{ {\dfrac{5}{4}} \right\}\)
-
C.
\(S = \left\{ { - 1} \right\}\)
-
D.
\(S = \left\{ 0 \right\}\)
Đáp án : A
Sử dụng quy tắc chuyển vế để biến đổi đưa phương trình về dạng phương trình bậc nhất một ẩn \(ax + b = 0 \Leftrightarrow x = - \dfrac{b}{a}\,\left( {a \ne 0} \right)\).
Ta có: \(7x + 4\; = 3x-{\rm{ }}1\)
\(\begin{array}{l} \Leftrightarrow 7x - 3x = - 1 - 4\\ \Leftrightarrow 4x = - 5\\ \Leftrightarrow x = - \dfrac{5}{4}\end{array}\).
Vậy phương trình có tập nghiệm là \(S = \left\{ {\dfrac{{ - 5}}{4}} \right\}\).
Khi \(x \ge 3\), kết quả rút gọn của biểu thức \(2{\rm{x}} + \left| {x - 3} \right| - 1\) là:
-
A.
\(3x + 2\)
-
B.
\(3x - 4\)
-
C.
\(x + 2\)
-
D.
\(4 - 3x\)
Đáp án : B
Áp dụng định nghĩa giá trị tuyệt đối của một số hữu tỉ để rút gọn biểu thức: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,khi\,\,x \ge 0\\ - x\,\,khi\,\,x < 0\end{array} \right.\)
Khi \(x \ge 3\) thì \(\left| {x - 3} \right| = x - 3,\) ta có biểu thức:
\(2x + \left| {x - 3} \right| - 1 = 2x + x - 3 - 1 = 3x - 4.\)
Cho \(\Delta MNP \backsim \Delta HGK\) có tỉ số chu vi: \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}.\) Chọn câu đúng.
-
A.
\(\dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)
-
B.
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{2}{7}\)
-
C.
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{{49}}{4}\)
-
D.
\(\dfrac{{NP}}{{GK}} = \dfrac{5}{7}\)
Đáp án : A
+) Áp dụng lý thuyết về mối quan hệ giữa tỉ số diện tích hai tam giác đồng dạng và tỉ số đồng dạng của 2 tam giác, kết hợp với dữ kiện đề bài cho để thực hiện yêu cầu của bài toán.
Lưu ý: Tỉ số đồng dạng bằng tỉ số chu vi và tỉ số diện tích bằng bình phương tỉ số đồng dạng.
Gọi k là tỉ số đồng dạng của 2 tam giác MNP và HGK.
Theo bài ta có:
\(\Delta MNP \backsim \Delta HGK\) và \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}\)
\( \Rightarrow \dfrac{{MN}}{{HG}} = \dfrac{{NP}}{{GK}} = \dfrac{{MP}}{{HK}} \)\(=\dfrac{MN+NP+MP}{HG+GK+HK}= \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7} = k\)
Do đó: \( \dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)
Và \( \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = {k^2} = {\left( {\dfrac{2}{7}} \right)^2} = \dfrac{4}{{49}}.\)
Giá trị \(x = 2\) là nghiệm của bất phương trình nào dưới đây?
-
A.
\(2x + 5 > 11\)
-
B.
\(4-x > 3x-1\)
-
C.
\( - 4{\rm{x}} + 7 > x - 1\)
-
D.
\({x^2} + 3 > 6x-7\)
Đáp án : D
Giải các bất phương trình ở các đáp án sau đó xem \(x = 2\) có thuộc tập nghiệm của bất phương trình nào thì chọn đáp án đó.
Ta có:
+) Đáp án A: \(2x + 5 > 11 \Leftrightarrow 2x > 6 \)\(\Leftrightarrow x > 3 \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.
+) Đáp án B: \(4 - x > 3x - 1 \Leftrightarrow 4 + 1 > 3x + x \Leftrightarrow 4x < 5\)\( \Leftrightarrow x < \dfrac{5}{4} \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.
+) Đáp án C: \( - 4x + 7 > x - 1 \Leftrightarrow 7 + 1 > x + 4x \Leftrightarrow 5x < 8\)\( \Leftrightarrow x < \dfrac{8}{5} \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.
+) Đáp án D: \({x^2} + 3 > 6x - 7 \Leftrightarrow {x^2} - 6x + 10 > 0\)
Thay \(x = 2\) vào vế trái của bất phương trình ta có: \({2^2} - 6.2 + 10 = 2 > 0\) (luôn đúng)
\( \Rightarrow x = 2\) là nghiệm của bất phương trình.
Rút gọn biểu thức \({\left( {x + y} \right)^2} + {\rm{ }}{\left( {x - y} \right)^2}\), ta được kết quả là:
-
A.
\(2\left( {{x^2} + {\rm{ }}{y^2}} \right)\)
-
B.
\(2{x^2} + {\rm{ }}{y^2}\)
-
C.
\(2\left( {{x^2} - {\rm{ }}{y^2}} \right)\)
-
D.
Một kết quả khác
Đáp án : A
Sử dụng các hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2};\,{\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\).
Ta có: \({\left( {x + y} \right)^2} + {\rm{ }}{\left( {x - y} \right)^2}\)\( = {x^2} + 2xy + {y^2} + {x^2} - 2xy + {y^2}\)\( = 2{x^2} + 2{y^2} = 2\left( {{x^2} + {y^2}} \right)\).
Phương trình \(\left| {x - 4} \right| + 3x = 5\) có tổng các nghiệm là:
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{{11}}{4}\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(1\)
Đáp án : C
Sử dụng \(\left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\,A < 0\end{array} \right.\) để đưa về phương trình bậc nhất một ẩn.
Xét phương trình \(\left| {x - 4} \right| + 3x = 5\).
TH1: \(\left| {x - 4} \right| = x - 4\) với \(x - 4 \ge 0 \Leftrightarrow x \ge 4\)
Khi đó ta có phương trình: \(x - 4 + 3x = 5 \Leftrightarrow 4x = 9 \Leftrightarrow x = \dfrac{9}{4}\) (loại vì \(x \ge 4\))
TH2: \(\left| {x - 4} \right| = - x + 4\) với \(x - 4 < 0 \Leftrightarrow x < 4\)
Khi đó ta có phương trình \( - x + 4 + 3x = 5\)\( \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}\) (nhận)
Vậy phương trình đã cho có một nghiệm là \(x = \dfrac{1}{2}.\)
Phương trình \({x^3} - 9x = 0\) có bao nhiêu nghiệm?
-
A.
\(1\)
-
B.
\(3\)
-
C.
\(4\)
-
D.
\(2\)
Đáp án : B
Phân tích vế trái thành nhân tử đưa phương trình về dạng \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)
Ta có: \({x^3} - 9x = 0\)\( \Leftrightarrow x\left( {{x^2} - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 9 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\\x = - 3\end{array} \right.\)
Vậy phương trình có tập nghiệm \(S = \left\{ { - 3;0;3} \right\}\).
Hay phương trình đã cho có ba nghiệm phân biệt.
Cho hình vẽ, biết \(DE// BC\). Khẳng định nào sau đây là đúng ?

-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\)
-
B.
\(AD.AE = AB.AC\)
-
C.
\(\dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC}}\)
-
D.
\(DE.AD = AB.BC\)
Đáp án : A
Áp dụng định lý Talet để tìm ra tỉ lệ thức phù hợp, từ đó thực hiện yêu cầu của bài toán.
Áp dụng định lý Ta lét, ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow \) Đáp án A đúng.
Vì \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) nên \(AD.AC = AB.AE\)
\( \Rightarrow \) Đáp án B sai.
Ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow \)\(\dfrac{{AD}}{{AB - AD}} = \dfrac{{DE}}{{BC}} \Leftrightarrow \dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC - DE}}\)
\( \Rightarrow \) Đáp án C sai.
Ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow AD.BC = AB.DE\)
\( \Rightarrow \) Đáp án D sai.
Diện tích toàn phần của hình lập phương có độ dài cạnh đáy bằng 5cm là:
-
A.
\(25\,c{m^2}\)
-
B.
\(125\,c{m^2}\)
-
C.
\(150\,c{m^2}\)
-
D.
\(250\,c{m^2}\)
Đáp án : C
Công thức tính diện tích toàn phần của hình lập phương cạnh \(a\) là: \(6{a^2}.\)
Diện tích toàn phần của hình lập phương có độ dài cạnh đáy bằng 5cm là: \({S_{tp}} = {6. 5^2} = 150\,c{m^2}.\)
Một người đi xe máy từ A đến B với vận tốc trung bình 30km/giờ. Khi đi được 1 giờ thì xe bị hỏng, người đó phải dừng lại để sửa xe mất 10 phút. Sau khi sửa xong người đó đi tiếp tới B, để đến B đúng giờ đã định người đó phải tăng vận tốc thêm 6km/h. Tính độ dài quãng đường AB.
-
A.
\(60\,km\)
-
B.
\(120\,km\)
-
C.
\(90\,km\)
-
D.
\(150\,km\)
Đáp án : A
Giải theo các bước sau:
+ Lập phương trình: Chọn ẩn và đặt điều kiện; biểu diễn đại lượng chưa biết theo ẩn và đại lượng đã biết; lập phương trình biểu thị mối quan hệ giữa các đại lượng
+ Giải phương trình
+ Đối chiếu điều kiện rồi kết luận
Đổi 10 phút = \(\dfrac{1}{6}\) giờ.
Gọi quãng đường AB dài là \(x\left( {km} \right)\left( {x > 30{\rm{ }}} \right)\).
Suy ra quãng đường từ khi dừng lại sửa xe đến B là \(x- 30{\rm{ }}\left( {km} \right)\).
Thời gian dự định đi từ A đến B là \(\dfrac{x}{{30}}\)(h).
Thời gian thực tế đi từ A đến B là \(1 + \dfrac{1}{6} + \dfrac{{x - 30}}{{36}}\) (h).
Ta có phương trình:
\(1 + \dfrac{1}{6} + \dfrac{{x - 30}}{{36}} = \dfrac{x}{{30}}\)
\( \Leftrightarrow \dfrac{{36 + 6 + x - 30}}{{36}} = \dfrac{x}{{30}}\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{12 + x}}{{36}} = \dfrac{x}{{30}}\\ \Rightarrow 30\left( {12 + x} \right) = 36.x\\ \Leftrightarrow 360 + 30x = 36x\\ \Leftrightarrow 6x = 360\\ \Leftrightarrow x = 60\left( {tm} \right)\end{array}\)
Vậy quãng đường \(AB\) dài \(60\) km.
Giải phương trình \(\dfrac{{x + 5}}{{x - 5}} - \dfrac{{x - 5}}{{x + 5}} = \dfrac{{20}}{{{x^2} - 25}}\) ta được nghiệm là:
-
A.
\(x = 5\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = -1\)
Đáp án : C
Sử dụng các bước giải phương trình chứa ẩn ở mẫu thức:
+ Tìm ĐKXĐ
+ Quy đồng mẫu rồi khử mẫu.
+ Giải phương trình vừa nhận được.
+ Đối chiếu điều kiện rồi kết luận nghiệm.
ĐKXĐ: \(x \ne \pm 5\)
Ta có: \(\dfrac{{x + 5}}{{x - 5}} - \dfrac{{x - 5}}{{x + 5}} = \dfrac{{20}}{{{x^2} - 25}}\).
\( \Leftrightarrow \dfrac{{{{\left( {x + 5} \right)}^2} - {{\left( {x - 5} \right)}^2}}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} = \dfrac{{20}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\)
\(\begin{array}{l} \Rightarrow {\left( {x + 5} \right)^2} - {\left( {x - 5} \right)^2} = 20\\ \Leftrightarrow {x^2} + 10x + 25 - {x^2} + 10x - 25 = 20\\ \Leftrightarrow 20x = 20\\ \Leftrightarrow x = 1\left( {tm} \right)\end{array}\)
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ 1 \right\}\).
Cho \(a,b,c > 0\) thỏa mãn: \(6a + 2b + 3c = 11.\) Tìm giá trị nhỏ nhất của biểu thức \(M = \dfrac{{2b + 3c + 16}}{{1 + 6a}} + \dfrac{{6a + 3c + 16}}{{1 + 2b}} + \dfrac{{6a + 2b + 16}}{{1 + 3c}}\).
-
A.
\(8\)
-
B.
\(9\)
-
C.
\(15\)
-
D.
\(11\)
Đáp án : C
Biến đổi để sử dụng bất đẳng thức \(\dfrac{a}{b} + \dfrac{b}{a} \ge 2\) với \(a,b > 0\).
Dấu “=” xảy ra khi \(a = b.\)
Đặt \(x = 1 + 6a; y = 1 + 2b; z = 1 + 3c\,\,\left( {x,y,z > 0} \right)\)
\( \Rightarrow x + y + z = 1 + 6a + 1 + 2b + 1 + 3c\)\( = 3 + \left( {6a + 2b + 3c} \right) = 3 + 11 = 14\)
Ta có: \(2b + 3c + 16 = y - 1 + z - 1 + 16 = y + z + 14\)
\(6a + 3c + 16 = x + z + 14\)
\(6a + 2b + 16 = x + y + 14\)
Từ đó: \(M = \dfrac{{z + y + 14}}{x} + \dfrac{{x + z + 14}}{y} + \dfrac{{x + y + 14}}{z}\)
\( = \dfrac{z}{x} + \dfrac{y}{x} + \dfrac{{14}}{x} + \dfrac{x}{y} + \dfrac{z}{y} + \dfrac{{14}}{y} + \dfrac{x}{z} + \dfrac{y}{z} + \dfrac{{14}}{z}\)
\( = \left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + \left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + \left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + 14\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\)
\( = \left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + \left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + \left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + \left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\)
\( = 2\left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + 2\left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + 2\left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + 3\)
Mặt khác: \(\dfrac{x}{y} + \dfrac{y}{x} \ge 2\) dấu “ = ” xảy ra khi và chỉ khi \(x = y\)
\(\dfrac{x}{z} + \dfrac{z}{x} \ge 2.\) Dấu “ = ” xảy ra khi và chỉ khi \(x = z\)
\(\dfrac{z}{y} + \dfrac{y}{z} \ge 2.\) Dấu “ = ” xảy ra khi và chỉ khi \(z = y\)
Khi đó: \(M \ge 2. 2 + 2. 2 + 2. 2 + 3 \Rightarrow M \ge 15.\) Dấu “ = ” xảy ra khi và chỉ khi \(x = y = z = 1\)
Suy ra: \(a = \dfrac{{11}}{{18}};b = \dfrac{{11}}{6};c = \dfrac{{11}}{9}.\)
Vậy \({M_{min}} = 15\) khi \(a = \dfrac{{11}}{{18}};b = \dfrac{{11}}{6};c = \dfrac{{11}}{9}.\)