Đề thi khảo sát chất lượng đầu năm Toán 9 - Đề số 2 — Không quảng cáo

Phương trình chứa ẩn ở mẫu có nghĩa khi các mẫu thức đều khác $0.$

Để phương trình có nghĩa: \(\left\{ \begin{array}{l}x + 2 \ne 0\\2 - x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne  - 2\\x \ne 2\end{array} \right..\)

Vậy điều kiện xác định của phương trình là: \(x \ne 2,\;x \ne  - 2.\)

Sử dụng phương pháp nhóm hạng tử để phân tích đa thức thành nhân tử.

\({x^2} + xy - x - y = x\left( {x + y} \right) - \left( {x + y} \right)\)\( = \left( {x - 1} \right)\left( {x + y} \right)\).

Giải từng bất đẳng thức trong 4 đáp án, chọn đáp án mà bất đẳng thức có nghiệm \(x =  - 2\) nằm trong tập nghiệm.

Xét từng đáp án ta có:

\(3x + 17 < 5 \Leftrightarrow 3x <  - 12 \Leftrightarrow x <  - 4 \Rightarrow \) A sai.

\( - 2x + 1 <  - 1 \Leftrightarrow  - 2x <  - 2 \Leftrightarrow x > 1 \Rightarrow \) B sai.

\(\dfrac{1}{2}x + 5 > 3,5 \Leftrightarrow \dfrac{1}{2}x >  - 1,5 \Leftrightarrow x >  - 3 \Rightarrow x =  - 2\)  là một nghiệm của bất phương trình \( \Rightarrow \) C đúng.

\(1 - 2x <  - 3 \Leftrightarrow  - 2x <  - 4 \Leftrightarrow x > 2 \Rightarrow \) D sai.

Sử dụng liên hệ giữa thứ tự và phép nhân:

+ Khi nhân hai vế của bất phương trình với một số dương thì ta giữ nguyên dấu bất phương trình.

+ Khi nhân hai vế của bất phương trình với một số âm thì ta đổi dấu bất phương trình.

Sử dụng liên hệ giữa thứ tự và phép cộng: Khi cộng hai vế của bất phương trình cùng một số thì ta giữ nguyên dấu bất phương trình.

Ta có: \(a \le b \Leftrightarrow  - \dfrac{3}{4}a \ge  - \dfrac{3}{4}b\) (vì \( - \dfrac{3}{4} < 0\)) nên A sai.

Vì \(a \le b \Leftrightarrow \dfrac{1}{2}a \le \dfrac{1}{2}b\) (vì \(\dfrac{1}{2} > 0\)) nên B đúng.

Vì \(a \le b \Leftrightarrow  - 5a \ge  - 5b\) (vì \( - 5 < 0\)) nên C đúng.

Vì \(a \le b \Leftrightarrow a + \left( { - 7} \right) \le b + \left( { - 7} \right)\)\( \Leftrightarrow a - 7 < b - 7\) nên D đúng.

Chuyển vế đưa phương trình về dạng \(\left| A \right| = B\,\,\left( {B \ge 0} \right) \Leftrightarrow \left[ \begin{array}{l}A = B\\A =  - B\end{array} \right.\)

\(\begin{array}{l}\;\;\;\;\left| {2x + 5} \right| - 3 = x\\ \Leftrightarrow \left| {2x + 5} \right| = x + 3\,\,\,\left( {x \ge  - 3} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x + 5 = x + 3\\2x + 5 =  - \left( {x + 3} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2\\2x + 5 =  - x - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2\\3x =  - 8\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2\,(tm)\\x =  - \dfrac{8}{3}\,(tm)\end{array} \right.\end{array}\) \(\)

Vậy tập nghiệm của phương trình là S = \(\left\{ { - 2;\dfrac{{ - 8}}{3}} \right\}\).\(\)

Sử dụng \(A\left( x \right). B\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)

Ta có: \((2x - 4)(2x - 1) = 0 \Leftrightarrow \left[ \begin{array}{l}2x - 4 = 0\\2x - 1 = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}2x = 4\\2x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = \dfrac{1}{2}\end{array} \right.\)

Vậy phương trình đã cho có tập nghiệm \(S = \left\{ {\dfrac{1}{2};2} \right\}\).

Sử dụng công thức tính thể tích hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là \(a,b,c\) là \(V = abc.\)

Hình hộp chữ nhật có chiều dài \(a = 6cm,\) chiều rộng \(b = 4cm\) và chiều cao \(c.\)

Thể tích hình hộp chữ nhật \(V = abc\) \( = 6.4.c\)

Theo đề bài ta có \(6.4.c = 192 \Leftrightarrow c = 8\,cm.\)

Vậy chiều cao cần tìm là \(8\,cm.\)

Bước 1. Lập phương trình:

Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;

Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;

Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

Gọi vận tốc của ô tô thứ nhất là \(x\;\left( {km/h} \right), \left( {x > 0} \right)\).

\( \Rightarrow \) Vận tốc của ô tô thứ hai là \(x + 20 \left( {km/h} \right)\).

Đổi: 7 giờ 30 phút = 7,5h; 10 giờ 30 phút = 10,5h.

Thời gian ô tô thứ nhất đi đến khi gặp ô tô thứ hai là \(10,5 - 6 = 4,5\;h.\)

Thời gian ô tô thứ hai đi đến khi gặp ô tô thứ nhất là  \(10,5 - 7,5 = 3\;h.\)

Theo bài ta có phương trình sau:

\(\begin{array}{l}\;\;\;4,5x = 3\left( {x + 20} \right)\\ \Leftrightarrow 4,5x = 3x + 60\\ \Leftrightarrow 1,5x = 60\\ \Leftrightarrow x = 40\;\left( {tm} \right)\end{array}\)

Vậy vận tốc ô tô thứ nhất là \(40km/h,\) vận tốc ô tô thứ hai là \(40 + 20 = 60\;km/h.\)

Biến đổi bất phương trình về dạng bất phương trình một ẩn và giải bất phương trình.

\(\begin{array}{l}\;\;\;\dfrac{{x - 1}}{2} + \dfrac{{2 - x}}{3} \le \dfrac{{3x - 3}}{4}\\ \Leftrightarrow \dfrac{{\left( {x - 1} \right).6}}{{2.6}} + \dfrac{{\left( {2 - x} \right).4}}{{3.4}} \le \dfrac{{\left( {3x - 3} \right).3}}{{4.3}}\\ \Leftrightarrow 6\left( {x - 1} \right) + 4\left( {2 - x} \right) \le 3\left( {3x - 3} \right)\\ \Leftrightarrow 6x - 6 + 8 - 4x \le 9x - 9\\ \Leftrightarrow 2x + 2 \le 9x - 9\\ \Leftrightarrow 9x - 2x \ge 2 + 9\\ \Leftrightarrow 7x \ge 11\\ \Leftrightarrow x \ge \dfrac{{11}}{7}\end{array}\)\(\).

Vậy tập nghiệm của bất phương trình là \(S = \left\{ {x|x \ge \dfrac{{11}}{7}} \right\}.\)

Ta có: \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số \(k\)\( \Rightarrow \dfrac{{{C_{\Delta ABC}}}}{{{C_{\Delta A'B'C'}}}} = \dfrac{{AB}}{{A'B'}} = k.\)

Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{3}{5}\).

\( \Rightarrow \dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{3}{5}\)\( \Rightarrow \dfrac{{{C_{\Delta ABC}}}}{{{C_{\Delta A'B'C'}}}} = \dfrac{3}{5} \Rightarrow {C_{\Delta ABC}} = \dfrac{3}{5}{C_{\Delta A'B'C'}}.\)

Mà chu vi của tam giác \({C_{\Delta A'B'C'}} = 60cm\) nên \({C_{\Delta ABC}} = \dfrac{3}{5}. 60 = 36cm\).

Áp dụng định lý Ta-let: “Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ”.

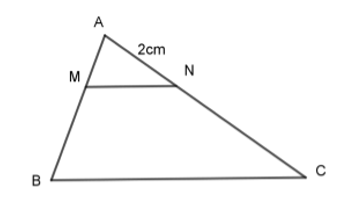
Theo bài ta có: \(AB = 3AM \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{1}{3}\).

Vì \(MN//BC,\) theo định lý Ta-let ta có:

\(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} \Leftrightarrow \dfrac{1}{3} = \dfrac{2}{{AC}} \Leftrightarrow AC = 2. 3 = 6cm\).

Áp dụng tính chất đường phân giác của một tam giác.

Đường phân giác trong của một tam giác chia cạnh đối diện thành hai đoạn thẳng tương ứng tỉ lệ với hai cạnh kề hai đoạn thẳng đó.

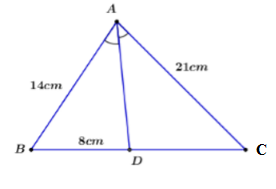
Vì AD là phân giác của tam giác ABC, theo tính chất của đường phân giác ta có:

\(\begin{array}{l}\dfrac{{AB}}{{B{\rm{D}}}} = \dfrac{{AC}}{{C{\rm{D}}}} \Leftrightarrow \dfrac{{14}}{8} = \dfrac{{21}}{{C{\rm{D}}}} \Leftrightarrow C{\rm{D}} = \dfrac{{8.21}}{{14}} = 12cm\\ \Rightarrow BC = B{\rm{D}} + DC = 8 + 12 = 20cm\end{array}\).

Áp dụng BĐT \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x,y > 0.\) Dấu xảy ra khi \(x = y > 0\)

Ta chứng minh bất đẳng thức \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x,y > 0.\)

Ta có \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}} \Leftrightarrow \dfrac{{x + y}}{{xy}} \ge \dfrac{4}{{x + y}}\)\( \Leftrightarrow {\left( {x + y} \right)^2} \ge 4xy \Leftrightarrow {x^2} - 2xy + {y^2} \ge 0\)\( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) đúng với mọi \(x,y > 0.\)

Nên ta có \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x,y > 0.\)

Áp dụng bất đẳng thức trên, ta được:

\(\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\) (1)

\(\dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{4}{{b + c}}\) (2)

\(\dfrac{1}{c} + \dfrac{1}{a} \ge \dfrac{4}{{c + a}}\) (3)

Cộng vế với vế của (1); (2); (3) ta có  \(2\left( {\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}} \right) \ge 4\left( {\dfrac{1}{{a + b}} + \dfrac{1}{{b + c}} + \dfrac{1}{{c + a}}} \right)\)

\( \Leftrightarrow \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{2}{{a + b}} + \dfrac{2}{{b + c}} + \dfrac{2}{{c + a}}\)

Dấu “ = ” xảy ra khi \(a = b = c > 0.\)