Đề thi khảo sát chất lượng đầu năm Toán 9 - Đề số 7
Đề bài
Cho tam giác $ABC$ có chu vi $18cm$ , các đường phân giác $BD$ và $CE$ . Tính các cạnh của tam giác $ABC$ , biết $\dfrac{{AD}}{{DC}} = \dfrac{1}{2},\dfrac{{AE}}{{EB}} = \dfrac{3}{4}$.
-
A.
$AC = 4\,cm,BC = 8\,cm,AB = 6\,cm$
-
B.
$AB = 4\,cm,BC = 6\,cm,AC = 8\,cm$
-
C.
$AB = 4\,cm,BC = 8\,cm,AC = 6\,cm$
-
D.
$AB = 8\,cm,BC = 4\,cm,AC = 6\,cm$
Chu vi một mảnh vườn hình chữ nhật là \(45\,m\) . Biết chiều dài hơn chiều rộng \(5\,m\) . Nếu gọi chiều rộng mảnh vườn là \(x\) \(\left( {x > 0;\,{\rm{m}}} \right)\) thì Phương trình của bài toán là
-
A.
\(\left( {2x + 5} \right).2 = 45\)
-
B.
\(x + 3\)
-
C.
\(3 - x\)
-
D.
\(3x\)
Lúc $7$ giờ một người đi xe máy khởi hành từ $A$ với vận tốc $30$ km/h. Sau đó một giờ, người thứ hai cũng đi xe máy từ $A$ đuổi theo với vận tốc $45$ km/h. Hỏi đến mấy giờ người thứ hai mới đuổi kịp người thứ nhất?
-
A.
\(7\) giờ
-
B.
\(8\) giờ
-
C.
\(10\) giờ
-
D.
\(9\) giờ
Có bao nhiêu nghiệm của phương trình \(\left| {x + 3} \right| = 7\)?
-
A.
\(2\)
-
B.
\(1\)
-
C.
\(0\)
-
D.
\(4\)
Phân thức \(\dfrac{{x + y}}{{{{\left( {x - y} \right)}^2}}}\) là kết quả của phép chia
-
A.
\(\dfrac{{{{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\) .
-
B.
\(\dfrac{{{{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^3}}}{{{{\left( {x + y} \right)}^3}}}\).
-
C.
\(\dfrac{{x - y}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\).
-
D.
\(\dfrac{{ - {{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\).
Gọi \({x_1};\,{x_2};{x_3}\) là các giá trị thỏa mãn \(4{\left( {3x - 5} \right)^2} - 9{\left( {9{x^2} - 25} \right)^2} = 0.\) Khi đó \({x_1} + {x_2} + {x_3}\) bằng
-
A.
\( - 3\).
-
B.
\( - \dfrac{3}{5}\).
-
C.
\( - \dfrac{5}{3}\).
-
D.
\( - \dfrac{5}{9}\).
Phân tích đa thức \(3x\left( {x - 3y} \right) + 9y\left( {3y - x} \right)\) thành nhân tử ta được
-
A.
$3{\left( {x - 3y} \right)^2}$.
-
B.
$\left( {x - 3y} \right)\left( {3x + 9y} \right)$.
-
C.
$\left( {x - 3y} \right) + \left( {3 - 9y} \right)$.
-
D.
$\left( {x - 3y} \right) + \left( {3x - 9y} \right)$.
Cho tam giác \(ABC\), lấy \(M\) thuộc \(BC\) sao cho \(BM = 3CM\). Hãy chọn câu sai :
-
A.
\({S_{ABM}} = \dfrac{3}{4}{S_{ABC}}\).
-
B.
\({S_{ABM}} = 3{S_{AMC}}\).
-
C.
\({S_{AMC}} = \dfrac{1}{3}{S_{ABC}}\).
-
D.
\({S_{ABC}} = 4{S_{AMC}}\).
Cho tứ giác \(ABCD\) . Tổng số đo các góc ngoài tại \(4\) đỉnh \(A,B,\,C,\,D\) là
-
A.
\(300^\circ \).
-
B.
\(270^\circ \).
-
C.
\(180^\circ \).
-
D.
\(360^\circ \).
Một xưởng dệt theo kế hoạch mỗi ngày phải dệt $30$ áo. Trong thực tế mỗi ngày xưởng dệt được $40$ áo nên đã hoàn thành trước thời hạn $3$ ngày, ngoài ra còn làm thêm được $20$ chiếc áo nữa. Hãy chọn câu đúng. Nếu gọi thời gian xưởng làm theo kế hoạch là \(x\) (ngày, \(x > 30\)). Thì phương trình của bài toán là:
-
A.
\(40x = 30\left( {x - 3} \right) - 20\).
-
B.
\(40x = 30\left( {x - 3} \right) + 20\).
-
C.
\(30x = 40\left( {x - 3} \right) + 20\).
-
D.
\(30x = 40\left( { x-3} \right) - 20\).
Cho hình thoi $ABCD$ có góc $A$ tù. Biết đường cao kẻ từ đỉnh $A$ đến cạnh $CD$ chia đôi cạnh đó. Tính các góc của hình thoi.
-
A.
$\widehat B = \widehat D = {80^0},\,\,\widehat A = \widehat C = {100^0}$
-
B.
$\widehat B = \widehat D = {120^0},\,\,\widehat A = \widehat C = {60^0}$
-
C.
$\widehat B = \widehat C = {60^0},\,\,\widehat A = \widehat D = {120^0}$
-
D.
$\widehat B = \widehat D = {60^0},\,\,\widehat A = \widehat C = {120^0}$
Hình thoi không có tính chất nào dưới đây?
-
A.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
-
B.
Hai đường chéo là các đường phân giác của các góc của hình thoi.
-
C.
Hai đường chéo bằng nhau.
-
D.
Hai đường chéo vuông góc với nhau.
Cho hình bình hành $ABCD$ có \(\widehat A = \alpha > 90^\circ \) . Ở phía ngoài hình bình hành vẽ các tam giác đều $ADE,ABF$. Tam giác \(CEF\) là tam giác gì? Chọn câu trả lời đúng nhất
-
A.
Tam giác vuông
-
B.
Tam giác cân
-
C.
Tam giác đều
-
D.
Tam giác tù
Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét .
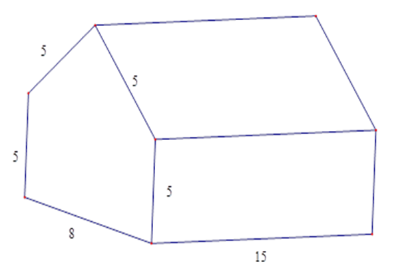
-
A.
\(870\,{m^3}\)
-
B.
\(700\,{m^3}\)
-
C.
\(680\,{m^3}\)
-
D.
\(780\,{m^3}\)
Tính thể tích của hình lăng trụ đứng có chiều cao $20\,{\rm{cm}}$, đáy là một tam giác vuông có các cạnh góc vuông bằng $8\,{\rm{cm}}$ và $10\,{\rm{cm}}$.
-
A.
\(800\,c{m^3}\)
-
B.
\(400\,c{m^3}\)
-
C.
\(600\,c{m^3}\)
-
D.
\(500\,c{m^3}\)
Cho tam giác \(\Delta ABC\backsim\Delta EDC\) như hình vẽ, tỉ số độ dài của $x$ và $y$ là:
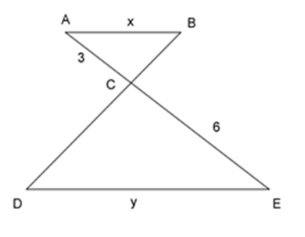
-
A.
$7 $
-
B.
\(\dfrac{1}{2}\)
-
C.
\(\dfrac{7}{4}\)
-
D.
\(\dfrac{7}{{16}}\)
Có bao nhiêu đa thức trong 4 biểu thức sau: \(2{x^2} - 3xy;\,\) \(2{x^2} - 3x + 1;\,\)\( - 3xy\) và \(\dfrac{{ - 1}}{{2x}}\) ?
-
A.
\(4\)
-
B.
\(3\)
-
C.
\(2\)
-
D.
\(1\)
Tìm $P$ biết: $P + \dfrac{{4x - 12}}{{{x^3} - 3{x^2} - 4x + 12}} = \dfrac{3}{{x - 3}} - \dfrac{{{x^2}}}{{4 - {x^2}}}$
-
A.
\(P = \dfrac{x}{{x + 3}}\)
-
B.
\(P = \dfrac{x}{{x - 3}}\)
-
C.
\(P = \dfrac{{2x}}{{x - 3}}\)
-
D.
\(P = \dfrac{{x - 3}}{x}\)
Cho phương trình: \(\left( {4{m^2} - 9} \right)x = 2{m^2} + m - 3\) . Tìm m để phương trình có vô số nghiệm
-
A.
\(m = - \dfrac{3}{2}\)
-
B.
$m = 1$
-
C.
\(m = \dfrac{3}{2}\)
-
D.
\(m = \dfrac{2}{3}\)
Phương trình \(\dfrac{{x - 1}}{2} + \dfrac{{x - 1}}{3} - \dfrac{{x - 1}}{6} = 2\) có tập nghiệm là
-
A.
\(S = \left\{ {0;1} \right\}\)
-
B.
\(S = \left\{ 4 \right\}\)
-
C.
\(S = \emptyset \)
-
D.
\(S = \mathbb{R}\)
Phương trình \(2x + k = x - 1\) nhận \(x = 2\) là nghiệm khi
-
A.
\(k = 3\)
-
B.
\(k = - 3\)
-
C.
\(k = 0\)
-
D.
\(k = 1\)
Cho đa thức: \(7{x^3} + 3{x^4} - x + 5{x^2} - 6{x^3} - 2{x^4} + 2020 + {x^3}\). Chỉ rõ hệ số cao nhất và hệ số tự do của đa thức.
-
A.
Hệ số cao nhất là: \(2020\), hệ số tự do là \(1\).
-
B.
Hệ số cao nhất là: \(2020\), hệ số tự do là \(2020\).
-
C.
Hệ số cao nhất là: \(3\), hệ số tự do là \(2020\).
-
D.
Hệ số cao nhất là: \(1\), hệ số tự do là \(2020\).
Tìm \(x\) biết \(\,{\left( {3x - \dfrac{1}{2}} \right)^2} + \dfrac{{21}}{{25}} = 1\).
-
A.
\(x = \dfrac{3}{8}\) hoặc \(x = \dfrac{1}{{30}}\)
-
B.
\(x = \dfrac{3}{{10}}\)
-
C.
\(x = \dfrac{3}{{10}}\) hoặc \(x = \dfrac{1}{{30}}\)
-
D.
\(x = \dfrac{1}{{30}}\)
Cho tam giác \(ABC\) có \(\widehat A = {70^0}\). Gọi \(I\) là giao điểm các tia phân giác \(\widehat B\) và \(\widehat C\). Số đo \(\widehat {BIC}\) là:
-
A.
\({135^0}\)
-
B.
\({115^0}\)
-
C.
\({125^0}\)
-
D.
\({105^0}\)
Tìm tổng \(x + {\rm{ }}y + {\rm{ }}z\) biết \(4{x^2} + 2{y^2} + 4{z^2} - 4xy-4y + 4z\; + 5 = 0\).
-
A.
\(5\)
-
B.
\(3\)
-
C.
\(\dfrac{5}{2}\)
-
D.
\(\dfrac{7}{2}\)
Lời giải và đáp án
Cho tam giác $ABC$ có chu vi $18cm$ , các đường phân giác $BD$ và $CE$ . Tính các cạnh của tam giác $ABC$ , biết $\dfrac{{AD}}{{DC}} = \dfrac{1}{2},\dfrac{{AE}}{{EB}} = \dfrac{3}{4}$.
-
A.
$AC = 4\,cm,BC = 8\,cm,AB = 6\,cm$
-
B.
$AB = 4\,cm,BC = 6\,cm,AC = 8\,cm$
-
C.
$AB = 4\,cm,BC = 8\,cm,AC = 6\,cm$
-
D.
$AB = 8\,cm,BC = 4\,cm,AC = 6\,cm$
Đáp án : C
Bước 1: Sử dụng tính chất đường phân giác của tam giác.
Bước 2: Sử dụng tính chất tỉ lệ thức để biến đổi.
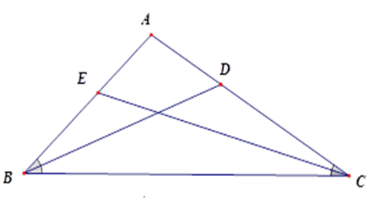
Theo tính chất đường phân giác, ta có
$\dfrac{{AB}}{{BC}} = \dfrac{{AD}}{{DC}} = \dfrac{1}{2},$
$\dfrac{{AC}}{{BC}} = \dfrac{{AE}}{{EB}} = \dfrac{3}{4}$nên
$\dfrac{{AB}}{2} = \dfrac{{BC}}{4} = \dfrac{{AC}}{3},$
Do đó $\dfrac{{AB}}{2} = \dfrac{{BC}}{4} = \dfrac{{AC}}{3} = \dfrac{{AB + BC + AC}}{{2 + 4 + 3}} = \dfrac{{18}}{9} = 2$.
Vậy $AB = 4\,cm,BC = 8\,cm,AC = 6\,cm.$
Chu vi một mảnh vườn hình chữ nhật là \(45\,m\) . Biết chiều dài hơn chiều rộng \(5\,m\) . Nếu gọi chiều rộng mảnh vườn là \(x\) \(\left( {x > 0;\,{\rm{m}}} \right)\) thì Phương trình của bài toán là
-
A.
\(\left( {2x + 5} \right).2 = 45\)
-
B.
\(x + 3\)
-
C.
\(3 - x\)
-
D.
\(3x\)
Đáp án : A
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết từ đó lập phương trình của bài toán.
Gọi chiều rộng mảnh vườn là \(x\) \(\left( {x > 0;\,{\rm{m}}} \right)\)
Vì chiều dài hơn chiều rộng \(5\,m\) nên chiều dài mảnh vườn là \(x + 5\,\) (m).
Vì chu vi mảnh vườn hình chữ nhật là \(45\,m\) nên ta có phương trình:
\(\left( {x + x + 5} \right).2 = 45 \)\(\Leftrightarrow 2\left( {2x + 5} \right) = 45\).
Lúc $7$ giờ một người đi xe máy khởi hành từ $A$ với vận tốc $30$ km/h. Sau đó một giờ, người thứ hai cũng đi xe máy từ $A$ đuổi theo với vận tốc $45$ km/h. Hỏi đến mấy giờ người thứ hai mới đuổi kịp người thứ nhất?
-
A.
\(7\) giờ
-
B.
\(8\) giờ
-
C.
\(10\) giờ
-
D.
\(9\) giờ
Đáp án : C
Giải theo các bước sau:
+ Lập phương trình: Chọn ẩn và đặt điều kiện; biểu diễn đại lượng chưa biết theo ẩn và đại lượng đã biết; lập Phương trình biểu thị mối quan hệ giữa các đại lượng
+ Giải phương trình
+ Đối chiếu điều kiện rồi kết luận
Gọi thời gian người thứ nhất đi đến khi gặp nhau là \(x\,\left( {x > 1} \right)\) (giờ)
Thì thời gian người thứ hai đi đến khi gặp nhau là \(x - 1\) (giờ)
Vì quãng đường hai người đi là bằng nhau nên ta có phương trình
\(30x = 45\left( {x - 1} \right) \Leftrightarrow 15x = 45 \Leftrightarrow x = 3\,\left( {TM} \right)\)
Vậy người thứ hai đuổi kịp người thứ nhất lúc \(7 + 3 = 10\) giờ.
Có bao nhiêu nghiệm của phương trình \(\left| {x + 3} \right| = 7\)?
-
A.
\(2\)
-
B.
\(1\)
-
C.
\(0\)
-
D.
\(4\)
Đáp án : A
Sử dụng các cách tìm \(x\) đã học để giải phương trình
\(\left| A \right| = B \Leftrightarrow \left[ \begin{array}{l}A = B\\A = - B\end{array} \right.\)
Ta có \(\left| {x + 3} \right| = 7\)\( \Leftrightarrow \left[ \begin{array}{l}x + 3 = 7\\x + 3 = - 7\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 10\end{array} \right.\)
Vậy phương trình có hai nghiệm \(x = 4;\,x = - 10\) .
Phân thức \(\dfrac{{x + y}}{{{{\left( {x - y} \right)}^2}}}\) là kết quả của phép chia
-
A.
\(\dfrac{{{{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\) .
-
B.
\(\dfrac{{{{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^3}}}{{{{\left( {x + y} \right)}^3}}}\).
-
C.
\(\dfrac{{x - y}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\).
-
D.
\(\dfrac{{ - {{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\).
Đáp án : A
Bước 1: Thực hiện phép chia hai phân thức: \(\dfrac{A}{B}:\dfrac{C}{D} = \dfrac{A}{B}.\dfrac{D}{C};\,\,\left( {\dfrac{C}{D} \ne 0} \right)\)
Bước 2: Rút gọn phân thức thu được.
Ta có: \(\dfrac{{{{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\)\( = \dfrac{{{{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}.\dfrac{{{{\left( {x + y} \right)}^3}}}{{{{\left( {x - y} \right)}^4}}} = \dfrac{{x + y}}{{{{\left( {x - y} \right)}^2}}}\) nên A đúng.
*) \(\dfrac{{{{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^3}}}{{{{\left( {x + y} \right)}^3}}}\)\( = \dfrac{{{{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}.\dfrac{{{{\left( {x + y} \right)}^3}}}{{{{\left( {x - y} \right)}^3}}} = \dfrac{{x + y}}{{x - y}}\) nên B sai.
*) \(\dfrac{{x - y}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\)\( = \dfrac{{x - y}}{{{{\left( {x + y} \right)}^2}}}.\dfrac{{{{\left( {x + y} \right)}^3}}}{{{{\left( {x - y} \right)}^4}}} = \dfrac{{x + y}}{{{{\left( {x - y} \right)}^3}}}\) nên C sai.
*) \(\dfrac{{ - {{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}:\dfrac{{{{\left( {x - y} \right)}^4}}}{{{{\left( {x + y} \right)}^3}}}\)$ = \dfrac{{ - {{\left( {x - y} \right)}^2}}}{{{{\left( {x + y} \right)}^2}}}.\dfrac{{{{\left( {x + y} \right)}^3}}}{{{{\left( {x - y} \right)}^4}}} = \dfrac{{ - \left( {x + y} \right)}}{{{{\left( {x - y} \right)}^2}}}$ nên D sai.
Gọi \({x_1};\,{x_2};{x_3}\) là các giá trị thỏa mãn \(4{\left( {3x - 5} \right)^2} - 9{\left( {9{x^2} - 25} \right)^2} = 0.\) Khi đó \({x_1} + {x_2} + {x_3}\) bằng
-
A.
\( - 3\).
-
B.
\( - \dfrac{3}{5}\).
-
C.
\( - \dfrac{5}{3}\).
-
D.
\( - \dfrac{5}{9}\).
Đáp án : C
+ Sử dụng hằng đẳng thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) để phân tích đa thức thành nhân tử.
+ Từ đó đưa về dạng \(A.B.C = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\\C = 0\end{array} \right.\)
Ta có \(4{\left( {3x - 5} \right)^2} - 9{\left( {9{x^2} - 25} \right)^2} = 0\)\( \Leftrightarrow 4.{\left( {3x - 5} \right)^2} - 9{\left[ {{{\left( {3x} \right)}^2} - {5^2}} \right]^2} = 0\)
\( \Leftrightarrow 4{\left( {3x - 5} \right)^2} - 9{\left[ {\left( {3x - 5} \right)\left( {3x + 5} \right)} \right]^2} = 0\)\( \Leftrightarrow 4{\left( {3x - 5} \right)^2} - 9{\left( {3x - 5} \right)^2}{\left( {3x + 5} \right)^2} = 0\)
\( \Leftrightarrow {\left( {3x - 5} \right)^2}\left[ {4 - 9{{\left( {3x + 5} \right)}^2}} \right] = 0\) \( \Leftrightarrow {\left( {3x - 5} \right)^2}\left[ {4 - {{\left( {3\left( {3x + 5} \right)} \right)}^2}} \right] = 0 \Leftrightarrow {\left( {3x - 5} \right)^2}\left( {{2^2} - {{\left( {9x + 15} \right)}^2}} \right) = 0\)
\( \Leftrightarrow {\left( {3x - 5} \right)^2}\left( {2 + 9x + 15} \right)\left( {2 - 9x - 15} \right) = 0\) \( \Leftrightarrow {\left( {3x - 5} \right)^2}\left( {9x + 17} \right)\left( { - 9x - 13} \right) = 0\)
$ \Leftrightarrow \left[ \begin{array}{l}3x - 5 = 0\\9x + 17 = 0\\ - 9x - 13 = 0\end{array} \right.$ \( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{5}{3}\\x = - \dfrac{{17}}{9}\\x = - \dfrac{{13}}{9}\end{array} \right.\) suy ra \({x_1} + {x_2} + {x_3} = \dfrac{5}{3} + \dfrac{{ - 17}}{9} + \dfrac{{ - 13}}{9} \)\(= - \dfrac{5}{3}\) .
Phân tích đa thức \(3x\left( {x - 3y} \right) + 9y\left( {3y - x} \right)\) thành nhân tử ta được
-
A.
$3{\left( {x - 3y} \right)^2}$.
-
B.
$\left( {x - 3y} \right)\left( {3x + 9y} \right)$.
-
C.
$\left( {x - 3y} \right) + \left( {3 - 9y} \right)$.
-
D.
$\left( {x - 3y} \right) + \left( {3x - 9y} \right)$.
Đáp án : A
+ Sử dụng tính chất \(A = - \left( { - A} \right)\) để xuất hiện nhân tử chung
+ Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử
Ta có \(3x\left( {x - 3y} \right) + 9y\left( {3y - x} \right) = 3x\left( {x - 3y} \right) - 9y\left( {x - 3y} \right)\)
\( = \left( {x - 3y} \right)\left( {3x - 9y} \right) = \left( {x - 3y} \right).3\left( {x - 3y} \right) = 3{\left( {x - 3y} \right)^2}\)
Cho tam giác \(ABC\), lấy \(M\) thuộc \(BC\) sao cho \(BM = 3CM\). Hãy chọn câu sai :
-
A.
\({S_{ABM}} = \dfrac{3}{4}{S_{ABC}}\).
-
B.
\({S_{ABM}} = 3{S_{AMC}}\).
-
C.
\({S_{AMC}} = \dfrac{1}{3}{S_{ABC}}\).
-
D.
\({S_{ABC}} = 4{S_{AMC}}\).
Đáp án : C
Bước 1: Sử dụng công thức: Diện tích tam giác bằng nửa tích một cạnh với chiều cao ứng với cạnh đó: \(S = \dfrac{1}{2}ah\)
Bước 2: Từ đó dựa vào dữ kiện \(BM = 3CM\) ta tìm được mối quan hệ diện tích giữa các tam giác.
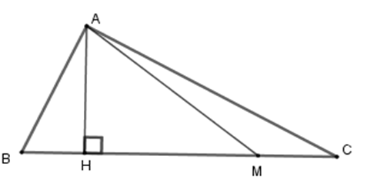
Kẻ \(AH \bot BC\) tại \(H\) .
Mà \(BM = 3CM\)\( \Rightarrow BM = \dfrac{3}{4}BC;\,CM = \dfrac{1}{4}BC;\,\)
Khi đó ta có
\(\begin{array}{l}{S_{ABM}} = \dfrac{1}{2}.\,AH.BM = \dfrac{1}{2}AH.\dfrac{3}{4}BC\\ = \dfrac{3}{4}.\left( {\dfrac{1}{2}AH.BC} \right) = \dfrac{3}{4}{S_{ABC}}\end{array}\)
Suy ra A đúng.
\(\begin{array}{l}{S_{AMB}} = \dfrac{1}{2}.\,AH.MB = \dfrac{1}{2}AH.3MC\\ = 3.\left( {\dfrac{1}{2}AH.MC} \right) = 3{S_{AMC}}\end{array}\)
Suy ra B đúng.
\(\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}.\,AH.BC = \dfrac{1}{2}AH.4MC = 4{S_{AMC}}\\ \Rightarrow {S_{ABC}} = 4{S_{AMC}} \Leftrightarrow {S_{AMC}} = \dfrac{1}{4}{S_{ABC}}\end{array}\)
suy ra D đúng, C sai.
Cho tứ giác \(ABCD\) . Tổng số đo các góc ngoài tại \(4\) đỉnh \(A,B,\,C,\,D\) là
-
A.
\(300^\circ \).
-
B.
\(270^\circ \).
-
C.
\(180^\circ \).
-
D.
\(360^\circ \).
Đáp án : D
Ta sử dụng định nghĩa: Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
Và định lý: Tổng bốn góc của một tứ giác bằng ${360^0}$ .
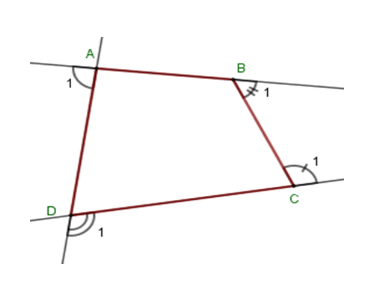
Gọi góc ngoài tại bốn đỉnh \(A,B,\,C,\,D\) của tứ giác \(ABCD\) lần lượt là \(\widehat {{A_1}};\,\widehat {{B_1}};\,\widehat {{C_1}};\,\widehat {{D_1}}\) . Khi đó ta có
\(\widehat A + \widehat {{A_1}} = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - \widehat A\); \(\widehat B + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - \widehat B\); \(\widehat C + \widehat {{C_1}} = 180^\circ \Rightarrow \widehat {{C_1}} = 180^\circ - \widehat C\) và \(\widehat D + \widehat {{D_1}} = 180^\circ \Rightarrow \widehat {{D_1}} = 180^\circ - \widehat D\)
Suy ra \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 180^\circ - \widehat A + 180^\circ - \widehat B + 180^\circ - \widehat C + 180^\circ - \widehat D\) \( = 720^\circ - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right) = 720^\circ - 360^\circ = 360^\circ \)
(Vì \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \))
Vậy tổng số đo các góc ngoài tại \(4\) đỉnh \(A,B,\,C,\,D\) là \(360^\circ \) .
Một xưởng dệt theo kế hoạch mỗi ngày phải dệt $30$ áo. Trong thực tế mỗi ngày xưởng dệt được $40$ áo nên đã hoàn thành trước thời hạn $3$ ngày, ngoài ra còn làm thêm được $20$ chiếc áo nữa. Hãy chọn câu đúng. Nếu gọi thời gian xưởng làm theo kế hoạch là \(x\) (ngày, \(x > 30\)). Thì phương trình của bài toán là:
-
A.
\(40x = 30\left( {x - 3} \right) - 20\).
-
B.
\(40x = 30\left( {x - 3} \right) + 20\).
-
C.
\(30x = 40\left( {x - 3} \right) + 20\).
-
D.
\(30x = 40\left( { x-3} \right) - 20\).
Đáp án : D
+) Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
+) Sau đó dựa vào giả thiết của đề bài để lập phương trình.
Gọi thời gian xưởng làm theo kế hoạch là \(x\) (ngày, \(x > 30\)).
Tổng số áo theo kế hoạch là \(30x\) (áo)
Vì đội hoàn thành trước thời hạn $3$ ngày nên thời gian làm theo thực tế là \(x - 3\) ngày.
Vì theo thực tế đội làm thêm được \(20\) sản phẩm nên ta có phương trình
\(40\left( {x - 3} \right) = 30x + 20\) \( \Leftrightarrow 40\left( {x - 3} \right) - 20 = 30x\).
Cho hình thoi $ABCD$ có góc $A$ tù. Biết đường cao kẻ từ đỉnh $A$ đến cạnh $CD$ chia đôi cạnh đó. Tính các góc của hình thoi.
-
A.
$\widehat B = \widehat D = {80^0},\,\,\widehat A = \widehat C = {100^0}$
-
B.
$\widehat B = \widehat D = {120^0},\,\,\widehat A = \widehat C = {60^0}$
-
C.
$\widehat B = \widehat C = {60^0},\,\,\widehat A = \widehat D = {120^0}$
-
D.
$\widehat B = \widehat D = {60^0},\,\,\widehat A = \widehat C = {120^0}$
Đáp án : D
+ Ta chứng minh tam giác $ADC$ là tam giác đều từ đó suy ra số đo góc $D$
+ Ta thấy góc $C$ và góc $D$ là hai góc bù nhau nên ta suy ra số đo góc$C$ .
+ Từ đó suy ra số đo hai góc còn lại.
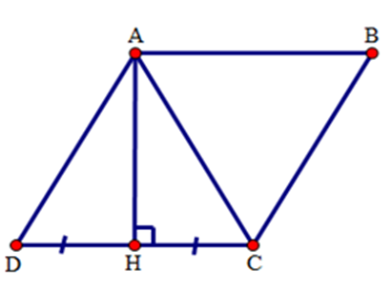
Gọi $H$ là chân đường cao kẻ từ $A$ đến cạnh $CD$ . Từ giả thiết ta có: \(AH \bot DC,CH = HD\) suy ra $AH$ là đường trung trục của đoạn $CD$ nên $AC = CD$ . (1)
Do $ABCD$ là hình thoi nên $AD = CD$ (2)
Từ (1) và (2) suy ra $AD = CD = AC$ nên tam giác $ACD$ là tam giác đều, do đó \(\widehat D = {60^0}\) .
Vì góc $A$ và góc $D$ là hai góc trong cùng phía của $AB$ // $CD$ nên chúng bù nhau hay \(\widehat A = {180^0} - {60^0} = {120^0}\).
Áp dụng tính chất về góc vào hình thoi ta được: $\widehat B = \widehat D = {60^0},\,\,\widehat A = \widehat C = {120^0}$.
Hình thoi không có tính chất nào dưới đây?
-
A.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
-
B.
Hai đường chéo là các đường phân giác của các góc của hình thoi.
-
C.
Hai đường chéo bằng nhau.
-
D.
Hai đường chéo vuông góc với nhau.
Đáp án : C
Hình thoi có tất cả các tính chất của hình bình hành
+ Các cạnh đối song song và bằng nhau, các góc đối bằng nhau
+ Hai đường chéo giao nhau tại trung điểm mỗi đường.
Ngoài ra còn có
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc của hình thoi.
Cho hình bình hành $ABCD$ có \(\widehat A = \alpha > 90^\circ \) . Ở phía ngoài hình bình hành vẽ các tam giác đều $ADE,ABF$. Tam giác \(CEF\) là tam giác gì? Chọn câu trả lời đúng nhất
-
A.
Tam giác vuông
-
B.
Tam giác cân
-
C.
Tam giác đều
-
D.
Tam giác tù
Đáp án : C
Chứng minh các tam giác bằng nhau để có các cạnh bằng nhau từ đó suy ra tam giác \(CEF\) là tam đều.
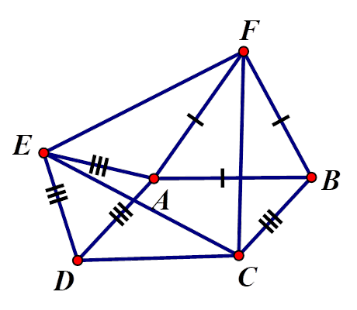
Ta có:
\(\widehat {EAF} = 360^\circ - \widehat {BAF} - \widehat {EAD} - \alpha \) \( = 360^\circ - 60^\circ - 60^\circ - \alpha = 240^\circ - \alpha \)
Ta có:\(\widehat {ADC} = 180^\circ - \alpha \) ; \(\widehat {CDE} = \widehat {ADC} + \widehat {EDA} = 180^\circ - \alpha + 60^\circ = 240^\circ - \alpha \)\( \Rightarrow \widehat {CDE} = \widehat {FAE}\)
Xét \(\Delta CDE\) và \(\Delta FAE\) có:
\(\left\{ \begin{array}{l}CD = FA(gt)\\\widehat {CDF} = \widehat {EAF}(cmt)\\DE = EA(gt)\end{array} \right.\)\( \Rightarrow \Delta CDE = \Delta FAE\left( {c.g.c} \right) \Rightarrow CE = FE\,\,(1)\)
Tương tự , ta có:
\(\widehat {ABC} = 180^\circ - \alpha \) ; \(\widehat {CBF} = \widehat {ABC} + \widehat {FBA} = 180^\circ - \alpha + 60^\circ = 240^\circ - \alpha \Rightarrow \widehat {CBF} = \widehat {FAE}\)
Xét \(\Delta FBC\) và \(\Delta FAE\) có:
\(\left\{ \begin{array}{l}FB = FA(gt)\\\widehat {CBF} = \widehat {EAF}(cmt)\\CB = EA(gt)\end{array} \right.\)\( \Rightarrow \Delta FBC = \Delta FAE\left( {c.g.c} \right) \Rightarrow CF = FE\,\,(2)\)
Từ (1) và (2) suy ra \(CF = FE = EC\) nên tam giác $CEF$ đều.
Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét .

-
A.
\(870\,{m^3}\)
-
B.
\(700\,{m^3}\)
-
C.
\(680\,{m^3}\)
-
D.
\(780\,{m^3}\)
Đáp án : D
+ Gọi $H$ là trung điểm $BC$. Tính $AH$ theo định lý Pytago từ đó suy ra diện tích đáy
+ Sử dụng công thức tính thể tích hình lăng trụ bằng tích diện tích đáy với chiều cao
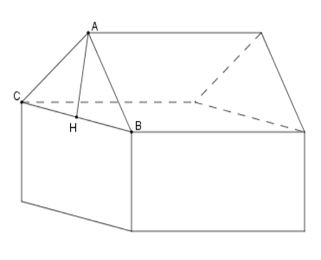
Gọi \(H\) là trung điểm \(BC \Rightarrow AH \bot BC\) . Ta có \(BH = 4;\,AB = 5\,m\)
Bằng định lí Py-ta-go ta tính được \(AH = \sqrt {A{B^2} - B{H^2}} = 3\,m\)
Diện tích đáy của hình lăng trụ bằng:
\(S = 5.8 + \dfrac{{8.3}}{2} = 52\left( {{m^2}} \right)\)
Thể tích nhà kho bằng
\(V = 52.15 = 780\left( {{m^3}} \right)\)
Tính thể tích của hình lăng trụ đứng có chiều cao $20\,{\rm{cm}}$, đáy là một tam giác vuông có các cạnh góc vuông bằng $8\,{\rm{cm}}$ và $10\,{\rm{cm}}$.
-
A.
\(800\,c{m^3}\)
-
B.
\(400\,c{m^3}\)
-
C.
\(600\,c{m^3}\)
-
D.
\(500\,c{m^3}\)
Đáp án : A
Sử dụng công thức tính thể tích hình lăng trụ đứng \(V = S.h\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Vì đáy là tam giác vuông nên diện tích đáy \(S = \dfrac{{8.10}}{2} = 40\,cm\) .
Thể tích lăng trụ đứng là \(V = S.h = 40.20 = 800\,c{m^3}\) .
Cho tam giác \(\Delta ABC\backsim\Delta EDC\) như hình vẽ, tỉ số độ dài của $x$ và $y$ là:

-
A.
$7 $
-
B.
\(\dfrac{1}{2}\)
-
C.
\(\dfrac{7}{4}\)
-
D.
\(\dfrac{7}{{16}}\)
Đáp án : B
Áp dụng lý thuyết về tam giác đồng dạng, ta suy ra tỉ lệ thức phù hợp, từ đó tìm ra tỉ lệ $x$ và $y$ .
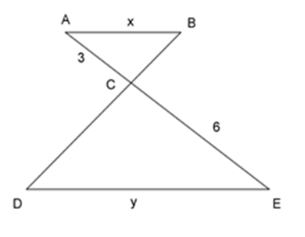
Ta có: \(\Delta ABC\backsim\Delta EDC\)
\( \Rightarrow \dfrac{{AB}}{{ED}} = \dfrac{{AC}}{{EC}} \Leftrightarrow \dfrac{x}{y} = \dfrac{3}{6} = \dfrac{1}{2}\)
Có bao nhiêu đa thức trong 4 biểu thức sau: \(2{x^2} - 3xy;\,\) \(2{x^2} - 3x + 1;\,\)\( - 3xy\) và \(\dfrac{{ - 1}}{{2x}}\) ?
-
A.
\(4\)
-
B.
\(3\)
-
C.
\(2\)
-
D.
\(1\)
Đáp án : B
Đa thức là một tổng của các đơn thức.
Trong 4 biểu thức trên chỉ có biểu thức \(\dfrac{{ - 1}}{{2x}}\) không phải đa thức.
Vậy có 3 đa thức trong 4 biểu thức trên.
Tìm $P$ biết: $P + \dfrac{{4x - 12}}{{{x^3} - 3{x^2} - 4x + 12}} = \dfrac{3}{{x - 3}} - \dfrac{{{x^2}}}{{4 - {x^2}}}$
-
A.
\(P = \dfrac{x}{{x + 3}}\)
-
B.
\(P = \dfrac{x}{{x - 3}}\)
-
C.
\(P = \dfrac{{2x}}{{x - 3}}\)
-
D.
\(P = \dfrac{{x - 3}}{x}\)
Đáp án : B
Sử dụng quy tắc chuyển vế, quy tắc đổi dấu, trừ các phân thức khác mẫu, phân tích đa thức thành nhân tử và rút gọn.
ĐK: $x \ne {\rm{\{ }} - 2;2;3\} $.
$\begin{array}{l}P + \dfrac{{4x - 12}}{{{x^3} - 3{x^2} - 4x + 12}} = \dfrac{3}{{x - 3}} - \dfrac{{{x^2}}}{{4 - {x^2}}}\\P = \dfrac{3}{{x - 3}} - \dfrac{{{x^2}}}{{4 - {x^2}}} - \dfrac{{4x - 12}}{{{x^3} - 3{x^2} - 4x + 12}}\\P = \dfrac{3}{{x - 3}} + \dfrac{{{x^2}}}{{(x - 2)(x + 2)}} - \dfrac{{4x - 12}}{{{x^2}(x - 3) - 4(x - 3)}}\\P = \dfrac{{3\left( {{x^2} - 4} \right)}}{{\left( {x - 3} \right)\left( {{x^2} - 4} \right)}} + \dfrac{{{x^2}\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {{x^2} - 4} \right)}} - \dfrac{{4x - 12}}{{\left( {x - 3} \right)\left( {{x^2} - 4} \right)}}\end{array}$
$P = \dfrac{{3{x^2} - 12 + {x^3} - 3{x^2} - 4x + 12}}{{\left( {x - 3} \right)\left( {{x^2} - 4} \right)}}$
$\begin{array}{l}P = \dfrac{{{x^3} - 4x}}{{(x - 3)(x - 2)(x + 2)}}\\P = \dfrac{{x({x^2} - 4)}}{{(x - 3)(x - 2)(x + 2)}} = \dfrac{x}{{x - 3}}\end{array}$
Cho phương trình: \(\left( {4{m^2} - 9} \right)x = 2{m^2} + m - 3\) . Tìm m để phương trình có vô số nghiệm
-
A.
\(m = - \dfrac{3}{2}\)
-
B.
$m = 1$
-
C.
\(m = \dfrac{3}{2}\)
-
D.
\(m = \dfrac{2}{3}\)
Đáp án : A
Phương trình \({\rm{ax}} = b\)
+ Có vô số nghiệm khi \(\left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\)
Phương trình
\(\begin{array}{l}\,\,\,\,\,\,\,\left( {4{m^2} - 9} \right)x = 2{m^2} + m - 3\\ \Leftrightarrow \left( {4{m^2} - 9} \right)x = 2{m^2} - 2m + 3m - 3\\ \Leftrightarrow \left( {2m - 3} \right)\left( {2m + 3} \right)x = 2m\left( {m - 1} \right) + 3\left( {m - 1} \right)\\ \Leftrightarrow \left( {2m - 3} \right)\left( {2m + 3} \right)x = \left( {m - 1} \right)\left( {2m + 3} \right)\end{array}\)
Phương trình có vô số nghiệm khi:
+) \(\left( {2m - 3} \right)\left( {2m + 3} \right) = 0\)
\(2m - 3 = 0\) hoặc \(2m + 3 = 0\)
\(m = \dfrac{3}{2}\) hoặc \(m = - \dfrac{3}{2}\) (1)
+) \(\left( {m - 1} \right)\left( {2m + 3} \right) = 0\)
\(m - 1 = 0\) hoặc \(2m + 3 = 0\)
\(m = 1\) hoặc \(m = - \dfrac{3}{2}\) (2)
Từ (1) và (2) suy ra \(m = - \dfrac{3}{2}\)
Vậy phương trình có vô số nghiệm khi \(m = - \dfrac{3}{2}.\)
Phương trình \(\dfrac{{x - 1}}{2} + \dfrac{{x - 1}}{3} - \dfrac{{x - 1}}{6} = 2\) có tập nghiệm là
-
A.
\(S = \left\{ {0;1} \right\}\)
-
B.
\(S = \left\{ 4 \right\}\)
-
C.
\(S = \emptyset \)
-
D.
\(S = \mathbb{R}\)
Đáp án : B
Vế trái đặt nhân tử chung rồi đưa phương trình về dạng phương trình bậc nhất một ẩn
\(\begin{array}{l}\dfrac{{x - 1}}{2} + \dfrac{{x - 1}}{3} - \dfrac{{x - 1}}{6} = 2\\ \dfrac{{1}}{2} (x-1) + \dfrac{1}{3}(x-1) - \dfrac{1}{6}(x-1) = 2\\\\\left( {x - 1} \right)\left( {\dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{6}} \right) = 2\\\left( {x - 1} \right)\dfrac{4}{6} = 2\\x - 1= 3\\x= 4\\S = \left\{ 4 \right\}\end{array}\)
Phương trình \(2x + k = x - 1\) nhận \(x = 2\) là nghiệm khi
-
A.
\(k = 3\)
-
B.
\(k = - 3\)
-
C.
\(k = 0\)
-
D.
\(k = 1\)
Đáp án : B
Thay giá trị của nghiệm vào phương trình đã cho ta được phương trình ẩn $k,$ giải phương trình để tìm ra $k.$
Thay \(x = 2\) vào phương trình ta được: \(2.2 + k = 2 - 1 \) suy ra \( k = - 3\)
Cho đa thức: \(7{x^3} + 3{x^4} - x + 5{x^2} - 6{x^3} - 2{x^4} + 2020 + {x^3}\). Chỉ rõ hệ số cao nhất và hệ số tự do của đa thức.
-
A.
Hệ số cao nhất là: \(2020\), hệ số tự do là \(1\).
-
B.
Hệ số cao nhất là: \(2020\), hệ số tự do là \(2020\).
-
C.
Hệ số cao nhất là: \(3\), hệ số tự do là \(2020\).
-
D.
Hệ số cao nhất là: \(1\), hệ số tự do là \(2020\).
Đáp án : D
Thu gọn đa thức một biến bằng cách thực hiện nhóm các hạng tử đồng dạng rồi cộng các đơn thức đồng dạng với nhau.
Từ đó xác định hệ số cao nhất và hệ số tự do của đa thức đó.
Ta có:
\(\begin{array}{l}7{x^3} + 3{x^4} - x + 5{x^2} - 6{x^3} - 2{x^4} + 2020 + {x^3}\\ = 3{x^4} - 2{x^4} + 7{x^3} - 6{x^3} + {x^3} - x + 2020\\ = {x^4} + 2{x^3} - x + 2020\end{array}\).
Hệ số cao nhất là: \(1\), hệ số tự do là \(2020\).
Tìm \(x\) biết \(\,{\left( {3x - \dfrac{1}{2}} \right)^2} + \dfrac{{21}}{{25}} = 1\).
-
A.
\(x = \dfrac{3}{8}\) hoặc \(x = \dfrac{1}{{30}}\)
-
B.
\(x = \dfrac{3}{{10}}\)
-
C.
\(x = \dfrac{3}{{10}}\) hoặc \(x = \dfrac{1}{{30}}\)
-
D.
\(x = \dfrac{1}{{30}}\)
Đáp án : C
Chuyển \(\dfrac{{21}}{{25}}\) của vế trái sang vế phải đổi dấu thành \(\dfrac{{ - 21}}{{25}}\), rồi thực hiện phép tính bên vế phải để tìm \({\left( {3x - \dfrac{1}{2}} \right)^2}\), rồi biến đổi kết quả vế phải về dạng bình phương của một số. Từ đó tìm ra x.
Ta có:
\(\begin{array}{l}\,{\left( {3x - \dfrac{1}{2}} \right)^2} + \dfrac{{21}}{{25}} = 1\\\,\,{\left( {3x - \dfrac{1}{2}} \right)^2}\,\,= 1 - \dfrac{{21}}{{25}}\\\,\,\,{\left( {3x - \dfrac{1}{2}} \right)^2}\,\,\, = \dfrac{4}{{25}}\\\,\,\,{\left( {3x - \dfrac{1}{2}} \right)^2}\,\,\, = \,{\left( { \pm \dfrac{2}{5}} \right)^2}\end{array}\)
TH1:
\(\begin{array}{l}3x - \dfrac{1}{2} = \dfrac{2}{5}\\3x\,\,\, = \dfrac{2}{5} + \dfrac{1}{2} = \dfrac{9}{{10}}\\\,\,\,x\,\,\, = \dfrac{9}{{10}}:3\\\,\,\,x\,\,\, = \dfrac{3}{{10}}\end{array}\)
TH2:
\(\begin{array}{l}3x - \dfrac{1}{2} = - \dfrac{2}{5}\\3x\,\,\, = - \dfrac{2}{5} + \dfrac{1}{2} = \dfrac{1}{{10}}\\\,\,\,x\,\,\, = \dfrac{1}{{10}}:3\\\,\,\,x\,\,\, = \dfrac{1}{{30}}\end{array}\)
Vậy \(x = \dfrac{3}{{10}}\) hoặc \(x = \dfrac{1}{{30}}\).
Cho tam giác \(ABC\) có \(\widehat A = {70^0}\). Gọi \(I\) là giao điểm các tia phân giác \(\widehat B\) và \(\widehat C\). Số đo \(\widehat {BIC}\) là:
-
A.
\({135^0}\)
-
B.
\({115^0}\)
-
C.
\({125^0}\)
-
D.
\({105^0}\)
Đáp án : C
Áp dụng tính chất tia phân giác và định lý: Tổng ba góc trong tam giác bằng \(180^0.\)
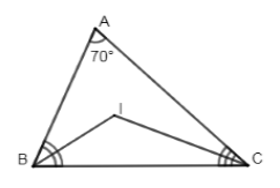
Vì \(BI\) và \(CI\) là tia phân giác của \(\angle ABC\) và \(\angle ACB\,\,\left( {gt} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}\angle IBC = \dfrac{1}{2}\angle ABC\\\angle ICB = \dfrac{1}{2}\angle ACB\end{array} \right.\) (tính chất tia phân giác)
\( \Rightarrow \angle IBC + \angle ICB = \dfrac{1}{2}\left( {\angle ABC + \angle ACB} \right) = \dfrac{1}{2}\left( {{{180}^0} - \angle A} \right) = \dfrac{1}{2}\left( {{{180}^0} - {{70}^0}} \right) = \dfrac{1}{2}{.110^0} = {55^0}\)
Xét \(\Delta BIC\) có: \(\angle BIC + \angle IBC + \angle ICB = {180^0}\) (tổng ba góc trong tam giác)
\( \Rightarrow \angle BIC = {180^0} - \left( {\angle IBC + \angle ICB} \right) = {180^0} - {55^0} = {125^0}\).
Tìm tổng \(x + {\rm{ }}y + {\rm{ }}z\) biết \(4{x^2} + 2{y^2} + 4{z^2} - 4xy-4y + 4z\; + 5 = 0\).
-
A.
\(5\)
-
B.
\(3\)
-
C.
\(\dfrac{5}{2}\)
-
D.
\(\dfrac{7}{2}\)
Đáp án : C
Sử dụng các hằng đẳng thức để đưa về dạng \({A^2} + {B^2} + {C^2} = 0 \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\\C = 0\end{array} \right.\)
Ta có: \(4{x^2} + 2{y^2} + 4{z^2} - 4xy--4y + 4z\; + 5 = 0\)
\( \Leftrightarrow \left( {4{x^2} - 4xy + {y^2}} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {4{z^2} + 4z + 1} \right) = 0\)
\( \Leftrightarrow {\left( {2x--y} \right)^2} + {\left( {y-2{\rm{ }}} \right)^2} + {\left( {2z + 1} \right)^2} = 0\) (*)
Mà \({\left( {2x - y} \right)^2} \ge 0;{\left( {y - 2} \right)^2} \ge 0;{\left( {2z + 1} \right)^2} \ge 0\) với mọi \(x;y;z\). Nên từ (*) suy ra:
\(\left\{ \begin{array}{l}{\left( {2x - y} \right)^2} = 0\\{\left( {y - 2} \right)^2} = 0\\{\left( {2z + 1} \right)^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = 0\\y - 2 = 0\\2z + 1 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{y}{2}\\y = 2\\z = - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\\z = - \dfrac{1}{2}\end{array} \right.\)
Suy ra: \(x + y + z = 1 + 2 + \left( { - \dfrac{1}{2}} \right) = \dfrac{5}{2}\).