Đề thi khảo sát chất lượng đầu năm Toán 9 - Đề số 8
Đề bài
Phương trình $\dfrac{{x - 12}}{{77}} + \dfrac{{x - 11}}{{78}}$$ = \dfrac{{x - 74}}{{15}} + \dfrac{{x - 73}}{{16}}$ có nghiệm là
-
A.
$x = 88$
-
B.
$x = 99$
-
C.
$x = 87$
-
D.
$x = 89$
Cho \(\Delta ABC\), đường phân giác góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,{\rm{ }}AD = 6{\rm{ }}cm.$ Tính $AC = $ ?
-
A.
$6{\rm{ }}cm$
-
B.
$9{\rm{ }}cm$
-
C.
$12{\rm{ }}cm$
-
D.
$15{\rm{ }}cm$
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều, $M$ là trung điểm của $BC,$ ${\rm{AA}}' = AM = a$. Thể tích của lăng trụ bằng:
-
A.
$\dfrac{{{a^2}\sqrt 3 }}{3}$
-
B.
$\dfrac{{{a^3}\sqrt 3 }}{3}$
-
C.
$\dfrac{{{a^3}\sqrt 2 }}{2}$
-
D.
$\dfrac{{a^3\sqrt 3}}{9}$
Tìm điều kiện xác định của phương trình:\(\begin{array}{l}\dfrac{{4x}}{{4{x^2} - 8x + 7}} + \dfrac{{3x}}{{4{x^2} - 10x + 7}} = 1\\\end{array}\)
-
A.
Mọi \(x \in R.\)
-
B.
\(x \ne 1\)
-
C.
\(x \ne 0;x \ne 1\)
-
D.
\(x \ne \dfrac{5}{4}\)
Nghiệm của bất phương trình $7(3x + 5) > 0$ là:
-
A.
$x > \dfrac{3}{5}$
-
B.
$x \le - \dfrac{5}{3}$
-
C.
$x \ge - \dfrac{5}{3}$
-
D.
$x > - \dfrac{5}{3}$.
Cho hình bình hành $ABCD,$ điểm $F$ nằm trên cạnh $BC.$ Tia $AF$ cắt $BD$ và $DC$ lần lượt ở $E$ và $G.$ Chọn câu đúng nhất.
-
A.
\(\Delta BFE \backsim \Delta DEA\)
-
B.
$\Delta DEG \backsim \Delta BAE$
-
C.
\(A{E^2} = GE.EF\)
-
D.
Cả A, B, C đều đúng.
Tích các nghiệm của phương trình $|{x^2} + 2x - 1| = 2$ là
-
A.
\(3\)
-
B.
\( - 3\)
-
C.
\(1\)
-
D.
\( - 1\).
Bất phương trình $\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x$ có nghiệm là:
-
A.
Vô nghiệm
-
B.
$x \ge 4,11$
-
C.
Vô số nghiệm
-
D.
$x \le - 5$
Tính thể tích của hình lăng trụ đứng có chiều cao $20\,{\rm{cm}}$, đáy là một tam giác vuông có các cạnh góc vuông bằng $8\,{\rm{cm}}$ và $10\,{\rm{cm}}$.
-
A.
\(800\,c{m^3}\)
-
B.
\(400\,c{m^3}\)
-
C.
\(600\,c{m^3}\)
-
D.
\(500\,c{m^3}\)
Tính giá trị của biểu thức \(B = {x^6} - 2{x^4} + {x^3} + {x^2} - x\) khi \({x^3} - x = 6\):
-
A.
$36$
-
B.
$42$
-
C.
$48$
-
D.
$56$
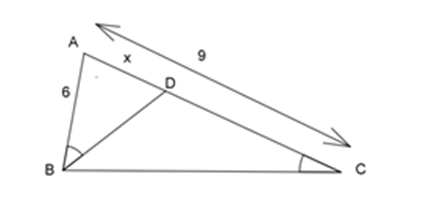
Cho hình bên biết $AB = 6\,cm,AC = 9\,cm$ , \(\widehat {ABD} = \widehat {BCA}\).
Độ dài đoạn $AD$ là:
-
A.
2 cm
-
B.
3 cm
-
C.
4 cm
-
D.
5 cm
Tam giác $ABC$ vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng $HA, HB.$
-
A.
\(HA = 2,4\,cm;\,HB = 1,2\,cm\)
-
B.
\(HA = 2\,cm;\,HB = 1,8\,cm\)
-
C.
\(HA = 2\,cm;\,HB = 1,2\,cm\)
-
D.
\(HA = 2,4\,cm;\,HB = 1,8\,cm\)
Rút gọn biểu thức \(A = \left( {{x^2} + 2 - 2x} \right)\left( {{x^2} + 2 + 2x} \right) - {x^4}\) ta được kết quả là:
-
A.
\(A = 4\)
-
B.
$A = - 4$
-
C.
\(A = 19\)
-
D.
\(A = - 19\)
Biết \({x_0}\) là nghiệm nhỏ nhất của phương trình
\(\dfrac{1}{{{x^2} + 4x + 3}} + \dfrac{1}{{{x^2} + 8x + 15}} + \dfrac{1}{{{x^2} + 12x + 35}} + \dfrac{1}{{{x^2} + 16x + 63}} = \dfrac{1}{5}.\) Chọn khẳng định đúng .
-
A.
\({x_0} > 0\)
-
B.
\({x_0} < - 5\)
-
C.
\({x_0} = - 10\)
-
D.
\({x_0} > 5\)
Cho hai điểm $A,B$ nằm trên cùng một nửa mặt phẳng bờ là đường thẳng $d$ . Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. Tìm trên đường thẳng $d$ điểm $M$ sao cho tổng $MA + MB$ nhỏ nhất. Chọn khẳng định đúng nhất.
-
A.
\(M\) là giao điểm của đoạn thẳng $AB$ và đường thẳng $d$.
-
B.
\(M\) là giao điểm của đoạn thẳng $AB'$ và đường thẳng $d$.
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai.
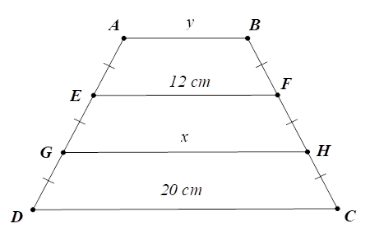
Tính \(x,y\) trên hình vẽ, trong đó \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\). Hãy chọn câu đúng.
-
A.
\(x = 8cm,y = 16cm\).
-
B.
\(x = 18cm,y = 9cm\).
-
C.
\(x = 18cm,y = 8cm\).
-
D.
\(x = 16cm,y = 8cm\).
Cho hình thang $ABCD\left( {AB{\rm{//}}CD} \right),$ đường cao $AH$, \(AB = 4\,cm,CD = 8\,cm,\) diện tích hình thang là \(54\,c{m^2}\) thì $AH$ bằng
-
A.
\(5\,cm\)
-
B.
\(4\,cm\)
-
C.
\(4,5\,cm\)
-
D.
\(9\,cm\)
Số đo mỗi góc trong và ngoài của ngũ giác đều là:
-
A.
\(75^\circ ;150^\circ \)
-
B.
\(108^\circ ;72^\circ \)
-
C.
\(100^\circ ;80^\circ \)
-
D.
\(110^\circ ;70^\circ \)
Một ô tô phải đi quãng đường $AB$ dài $60$ km trong một thời gian nhất định. Xe đi nửa đầu quãng đường với vận tốc hơn dự định $10$ km/h và đi với nửa sau kém hơn dự định $6$ km/h. Biết ô tô đến đúng dự định. Tính thời gian dự định đi quãng đường $AB$ ?
-
A.
\(3\) giờ
-
B.
\(6\) giờ
-
C.
\(5\) giờ
-
D.
\(2\) giờ
Cho \(a + 8 < b\). So sánh \(a - 7\) và \(b - 15\)
-
A.
\(a - 7 < b - 15\)
-
B.
\(a - 7 > b - 15\)
-
C.
\(a - 7 \ge b - 15\)
-
D.
\(a - 7 \le b - 15\)
Tập nghiệm của bất phương trình \(\left| {1 - x} \right| \ge 3\) là
-
A.
\(x \ge 4,x \le - 2\)
-
B.
\( - 2 \le x \le 4\)
-
C.
\(x \le - 2,x \le 4\)
-
D.
\(x \le 4,x \ge - 2\)
Hãy chọn câu đúng ?
Cho tam giác \(ABC\) có chu vi là \(32\) cm. Gọi \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\). Chu vi của tam giác \(EFP\) là
-
A.
\(17\,cm\).
-
B.
\(33\,cm\).
-
C.
\(15\,cm\).
-
D.
\(16\,cm\).
Tìm giá trị nguyên của \(x\) để phân thức \(\dfrac{3}{{x + 2}}\) có giá trị là một số nguyên.
-
A.
$x = - 3$
-
B.
\(x \in \left\{ { - 1;1} \right\}\)
-
C.
\(x \in \left\{ { - 1;1; - 5; - 3} \right\}\)
-
D.
$x = - 1$
Kết quả của phép chia \(\dfrac{{5\left( {x + 1} \right)}}{{x{y^2}}}:\dfrac{{10\left( {x + 1} \right)}}{{3{x^2}y}}\) là
-
A.
\(\dfrac{{50{{\left( {x + 1} \right)}^2}}}{{3{x^3}{y^3}}}\) .
-
B.
\(\dfrac{{3{x^2}}}{{2y}}\).
-
C.
\(\dfrac{{3x}}{{2y}}\).
-
D.
\(\dfrac{{3x}}{{2{y^2}}}\).
Thu gọn \(6{x^4}{y^2}:{\left( {\dfrac{1}{2}{x^2}y} \right)^2}\), ta được
-
A.
$12$
-
B.
$24$
-
C.
$24{x^2}y$
-
D.
$12{x^2}y$
Giá trị của biểu thức \(P = - 2{x^2}y\left( {xy + {y^2}} \right)\) tại \(x = - 1;\,y = 2\) là
-
A.
$8$
-
B.
$ - 8$
-
C.
$6$
-
D.
$ - 6$
Cho hai số tự nhiên \(n\) và \(m\). Biết rằng \(n\) chia \(5\) dư \(1\), \(m\) chia \(5\) dư \(4\). Hãy chọn câu đúng:
-
A.
\(m.n\) chia \(5\) dư \(1\)
-
B.
\(m - n\) chia hết cho \(5\)
-
C.
\(m + n\) chia hết cho \(5\)
-
D.
\(m.n\) chia \(5\) dư \(3\)
Phân tích đa thức \({x^3} + 12x\) thành nhân tử ta được
-
A.
\({x^2}\left( {x + 12} \right)\).
-
B.
\(x\left( {{x^2} + 12} \right)\).
-
C.
\(x\left( {{x^2} - 12} \right)\).
-
D.
\({x^2}\left( {x - 12} \right)\).
Cho \(x + n = 2\left( {y - m} \right),\)
khi đó giá trị của biểu thức \(A = {x^2} - 4xy + 4{y^2} - 4{m^2} - 4mn - {n^2}\) bằng
-
A.
\(A = 1\).
-
B.
\(A = 0\).
-
C.
\(A = 2\).
-
D.
Chưa đủ dữ kiện để tính.
Lời giải và đáp án
Phương trình $\dfrac{{x - 12}}{{77}} + \dfrac{{x - 11}}{{78}}$$ = \dfrac{{x - 74}}{{15}} + \dfrac{{x - 73}}{{16}}$ có nghiệm là
-
A.
$x = 88$
-
B.
$x = 99$
-
C.
$x = 87$
-
D.
$x = 89$
Đáp án : D
+ Trừ từng phân thức cho \(1\) rồi quy đồng để xuất hiện nhân tử chung.
+ Đặt nhân tử chung ra ngoài, rồi đánh giá và giải phương trình.
Ta có $\dfrac{{x - 12}}{{77}} + \dfrac{{x - 11}}{{78}} $$= \dfrac{{x - 74}}{{15}} + \dfrac{{x - 73}}{{16}}$
\( \Leftrightarrow \left( {\dfrac{{x - 12}}{{77}} - 1} \right) + \left( {\dfrac{{x - 11}}{{78}} - 1} \right) \)\(= \left( {\dfrac{{x - 74}}{{15}} - 1} \right) + \left( {\dfrac{{x - 73}}{{16}} - 1} \right)\)
\( \Leftrightarrow \left( {\dfrac{{x - 12 - 77}}{{77}}} \right) + \left( {\dfrac{{x - 11 - 78}}{{78}}} \right) \)\(= \left( {\dfrac{{x - 74 - 15}}{{15}}} \right) + \left( {\dfrac{{x - 73 - 16}}{{16}}} \right)\)
\( \Leftrightarrow \dfrac{{x - 89}}{{77}} + \dfrac{{x - 89}}{{78}} - \dfrac{{x - 89}}{{15}} - \dfrac{{x - 89}}{{16}} = 0\)
\( \Leftrightarrow \left( {x - 89} \right)\left( {\dfrac{1}{{77}} + \dfrac{1}{{78}} - \dfrac{1}{{15}} - \dfrac{1}{{16}}} \right) = 0\)
Nhận thấy \(\dfrac{1}{{77}} + \dfrac{1}{{78}} - \dfrac{1}{{15}} - \dfrac{1}{{16}} \ne 0\) nên \(\left( {x - 89} \right)\left( {\dfrac{1}{{77}} + \dfrac{1}{{78}} - \dfrac{1}{{15}} - \dfrac{1}{{16}}} \right) = 0 \)\(\Leftrightarrow x - 89 = 0 \Leftrightarrow x = 89\)
Cho \(\Delta ABC\), đường phân giác góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,{\rm{ }}AD = 6{\rm{ }}cm.$ Tính $AC = $ ?
-
A.
$6{\rm{ }}cm$
-
B.
$9{\rm{ }}cm$
-
C.
$12{\rm{ }}cm$
-
D.
$15{\rm{ }}cm$
Đáp án : D
- Áp dụng tính chất đường phân giác để tính DC.
- Từ đó tính $AC=AD+DC$
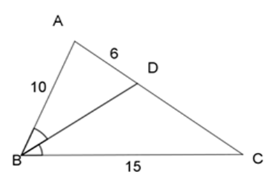
Áp dụng tính chất đường phân giác trong tam giác ABC, ta có: \(\dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CD}}\)
\( \Rightarrow \dfrac{{10}}{6} = \dfrac{{15}}{{CD}} \Leftrightarrow CD = \dfrac{{6.15}}{{10}} = 9\;cm\)
\( \Rightarrow AC = AD + DC = 6 + 9 = 15\;cm\)
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều, $M$ là trung điểm của $BC,$ ${\rm{AA}}' = AM = a$. Thể tích của lăng trụ bằng:
-
A.
$\dfrac{{{a^2}\sqrt 3 }}{3}$
-
B.
$\dfrac{{{a^3}\sqrt 3 }}{3}$
-
C.
$\dfrac{{{a^3}\sqrt 2 }}{2}$
-
D.
$\dfrac{{a^3\sqrt 3}}{9}$
Đáp án : B
- Áp dụng định lý Pytago và công thức tính thể tích hình lăng trụ đứng.
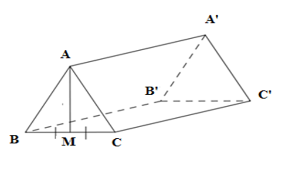
Vì tam giác $ABC$ là tam giác đều nên $AM$ vừa là trung tuyến vừa là đường cao của tam giác $ABC.$
Gọi chiều dài của cạnh tam giác $ABC$ là $x.\,\,\left( {x > 0} \right)$
\( \Rightarrow BM = MC = \dfrac{x}{2},\;AB = AC = BC = x\)
Xét tam giác vuông $MAC,$ ta có:
\(A{M^2} + M{C^2} = A{C^2} \Leftrightarrow {a^2} + \dfrac{{{x^2}}}{4} = {x^2} \Leftrightarrow \dfrac{{3{{\rm{x}}^2}}}{4} = {a^2} \Rightarrow x = \dfrac{{2\sqrt 3 }}{3}a\)
Vậy thể tích của hình lăng trụ là:
$V{\rm{ }} = {\rm{ }}{S_{ABC}}.h{\rm{ }} $ \(=\dfrac{1}{2}.AM.BC.AA' = \dfrac{1}{2}a.\dfrac{{2\sqrt 3 }}{3}a.a = \dfrac{{{a^3}\sqrt 3 }}{3}\)
Tìm điều kiện xác định của phương trình:\(\begin{array}{l}\dfrac{{4x}}{{4{x^2} - 8x + 7}} + \dfrac{{3x}}{{4{x^2} - 10x + 7}} = 1\\\end{array}\)
-
A.
Mọi \(x \in R.\)
-
B.
\(x \ne 1\)
-
C.
\(x \ne 0;x \ne 1\)
-
D.
\(x \ne \dfrac{5}{4}\)
Đáp án : A
ĐKXĐ của phương trình: đặt điều kiện cho ẩn để tất cả các mẫu trong phương trình đều khác 0.
ĐKXĐ:
\(\left\{ \begin{array}{l}4{x^2} - 8x + 7 \ne 0\\4{x^2} - 10x + 7 \ne 0\end{array} \right. \\ \left\{ \begin{array}{l}4{\left( {x - 1} \right)^2} + 3 > 0\\4\left( {x - \dfrac{5}{4}} \right)^2 + \dfrac{3}{4} > 0\end{array} \right. \\ \forall x \in \mathbb{R}\)
Vậy phương trình xác định với mọi \(x \in R.\)
Nghiệm của bất phương trình $7(3x + 5) > 0$ là:
-
A.
$x > \dfrac{3}{5}$
-
B.
$x \le - \dfrac{5}{3}$
-
C.
$x \ge - \dfrac{5}{3}$
-
D.
$x > - \dfrac{5}{3}$.
Đáp án : D
Giải bất phương trình tìm nghiệm phù hợp bằng cách dùng qui tắc nhân và qui tắc chuyển vế
Vì \(7 > 0\) nên \(7\left( {3x + 5} \right) \ge 3 \Leftrightarrow 3x + 5 > 0 \Leftrightarrow 3x > - 5 \Leftrightarrow x > - \dfrac{5}{3}.\)
Cho hình bình hành $ABCD,$ điểm $F$ nằm trên cạnh $BC.$ Tia $AF$ cắt $BD$ và $DC$ lần lượt ở $E$ và $G.$ Chọn câu đúng nhất.
-
A.
\(\Delta BFE \backsim \Delta DEA\)
-
B.
$\Delta DEG \backsim \Delta BAE$
-
C.
\(A{E^2} = GE.EF\)
-
D.
Cả A, B, C đều đúng.
Đáp án : C
- Áp dụng cách chứng minh tam giác đồng dạng để chứng minh các cặp tam giác đồng dạng.
- Từ đó tìm ra tỉ lệ thức phù hợp để suy ra hệ thức đúng về cạnh.
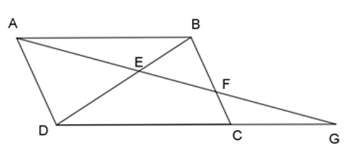
+) Vì $ABCD$ là hình bình hành nên \(AD//BC\)
\( \Rightarrow AD//BF\) (tính chất hbh).
Xét \(\Delta BEF\) và \(\Delta DEA\) có:
\(\widehat {BEF} = \widehat {DEA}\) (2 góc đối đỉnh)
\(\widehat {FBE} = \widehat {ADE}\) (cặp góc so le trong bằng nhau)
\( \Rightarrow \Delta BEF \backsim \Delta DEA\;(g - g)\) nên A sai.
+) Vì $ABCD$ là hình bình hành nên \(AB//DC\)
\( \Rightarrow AB//DG\)
Xét \(\Delta DGE\) và \(\Delta BAE\) ta có:
\(\widehat {DEG} = \widehat {BEA}\) (2 góc đối đỉnh)
\(\widehat {ABE} = \widehat {GDE}\) (cặp góc so le trong bằng nhau)
\( \Rightarrow \Delta DGE \backsim \Delta BAE\;(g - g)\) nên B sai.
+) Vì \(\Delta BEF \backsim \Delta DEA\) nên \(\dfrac{{EF}}{{EA}} = \dfrac{{BE}}{{DE}}\) (1)
Vì \(\Delta DGE \backsim \Delta BAE\) nên \(\dfrac{{AE}}{{GE}} = \dfrac{{BE}}{{DE}}\) (2)
Từ (1) và (2) ta có:
\(\dfrac{{EF}}{{EA}} = \dfrac{{AE}}{{GE}} \Leftrightarrow A{E^2} = GE.EF\) nên C đúng.
Tích các nghiệm của phương trình $|{x^2} + 2x - 1| = 2$ là
-
A.
\(3\)
-
B.
\( - 3\)
-
C.
\(1\)
-
D.
\( - 1\).
Đáp án : A
Sử dụng: Với $B(x) \ge 0$ thì
\(\left| {A(x)} \right| = B(x) \Rightarrow \left[ \begin{array}{l}A(x) = B(x)\\A(x) = - B(x)\end{array} \right.\)
\(\;\;\left| {{x^2} + 2x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 1 = 2\\{x^2} + 2x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 3 = 0\\{x^2} + 2x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} + 3x - x - 3 = 0\\{(x + 1)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x(x + 3) - (x + 3) = 0\\x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}(x + 3)(x - 1) = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x - 1 = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\\x = - 1\end{array} \right..\)
Vậy nghiệm của phương trình là $x{\rm{ }} = - 3;{\rm{ }}x = \pm 1.$
Tích các nghiệm của phương trình là \(\left( { - 3} \right).1.\left( { - 1} \right) = 3.\)
Bất phương trình $\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x$ có nghiệm là:
-
A.
Vô nghiệm
-
B.
$x \ge 4,11$
-
C.
Vô số nghiệm
-
D.
$x \le - 5$
Đáp án : D
- Áp dụng quy tắc chuyển vế - Quy đồng bỏ mẫu - Tìm $x$
Ta có: $\begin{array}{l}\;\;\;\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x\\ \Leftrightarrow \dfrac{{3(3x + 5)}}{6} - \dfrac{6}{6} \le \dfrac{{2(x + 2)}}{6} + \dfrac{{6x}}{6}\\ \Leftrightarrow 3(3x + 5) - 6 \le 2(x + 2) + 6x\\ \Leftrightarrow 9x + 15 - 6 \le 2x + 4 + 6x\\ \Leftrightarrow 9x - 2x - 6x \le 4 - 15 + 6\\ \Leftrightarrow x \le - 5.\end{array}$
Vậy nghiệm của bất phương trình là \(x \le - 5.\)
Tính thể tích của hình lăng trụ đứng có chiều cao $20\,{\rm{cm}}$, đáy là một tam giác vuông có các cạnh góc vuông bằng $8\,{\rm{cm}}$ và $10\,{\rm{cm}}$.
-
A.
\(800\,c{m^3}\)
-
B.
\(400\,c{m^3}\)
-
C.
\(600\,c{m^3}\)
-
D.
\(500\,c{m^3}\)
Đáp án : A
Sử dụng công thức tính thể tích hình lăng trụ đứng \(V = S.h\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Vì đáy là tam giác vuông nên diện tích đáy \(S = \dfrac{{8.10}}{2} = 40\,cm\) .
Thể tích lăng trụ đứng là \(V = S.h = 40.20 = 800\,c{m^3}\) .
Tính giá trị của biểu thức \(B = {x^6} - 2{x^4} + {x^3} + {x^2} - x\) khi \({x^3} - x = 6\):
-
A.
$36$
-
B.
$42$
-
C.
$48$
-
D.
$56$
Đáp án : B
+ Sử dụng phương pháp giao hoán, kết hợp và tách hạng tử (tách hạng tử thứ 2 thành 2 hạng tử giống nhau) để sắp xếp và tạo ra các hạng tử cần thiết.
+ Sau khi tách hạng tử, nhóm các hạng tử thích hợp để xuất hiện nhân tử chung giống với \({x^3} - x\).
+ Đặt nhân tử chung để được tích của các đa thức.
+ Sau đó thế biểu thức \({x^3} - x = 6\) vào biểu thức vừa biến đổi để tính giá trị biểu thức.
\(\begin{array}{l}\,\,\,\,\,\,\,\,B = {x^6} - 2{x^4} + {x^3} + {x^2} - x\\ \Leftrightarrow B = {x^6} - {x^4} - {x^4} + {x^3} + {x^2} - x\\ \Leftrightarrow B = \left( {{x^6} - {x^4}} \right) - \left( {{x^4} - {x^2}} \right) + \left( {{x^3} - x} \right)\\ \Leftrightarrow B = {x^3}\left( {{x^3} - x} \right) - x\left( {{x^3} - x} \right) + \left( {{x^3} - x} \right)\\ \Leftrightarrow B = \left( {{x^3} - x + 1} \right)\left( {{x^3} - x} \right)\end{array}\)
Tại \({x^3} - x = 6\), ta có: \(B = \left( {6 + 1} \right).6 = 7.6 = 42\)
Cho hình bên biết $AB = 6\,cm,AC = 9\,cm$ , \(\widehat {ABD} = \widehat {BCA}\).
Độ dài đoạn $AD$ là:

-
A.
2 cm
-
B.
3 cm
-
C.
4 cm
-
D.
5 cm
Đáp án : C
Bước 1: Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp góc – góc.
Bước 2: Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra giá trị của x.
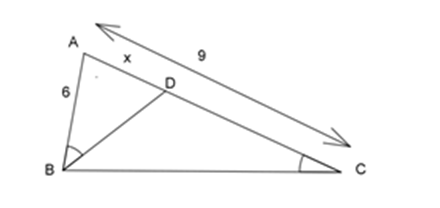
Xét \(\Delta ABD\) và \(\Delta ACB\) có:
\(\widehat A\;chung\)
\(\widehat {ABD} = \widehat {BCA}\;(gt)\)
\( \Rightarrow \Delta ABD\backsim\Delta ACB\;(g - g)\)
\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}} \Leftrightarrow \dfrac{6}{9} = \dfrac{x}{6} \Leftrightarrow x = \dfrac{{6.6}}{9} = 4\;cm\)
Tam giác $ABC$ vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng $HA, HB.$
-
A.
\(HA = 2,4\,cm;\,HB = 1,2\,cm\)
-
B.
\(HA = 2\,cm;\,HB = 1,8\,cm\)
-
C.
\(HA = 2\,cm;\,HB = 1,2\,cm\)
-
D.
\(HA = 2,4\,cm;\,HB = 1,8\,cm\)
Đáp án : D
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp.
- Tính độ dài các cạnh cần tìm dựa vào định lý Pitago và dữ kiện đã có.
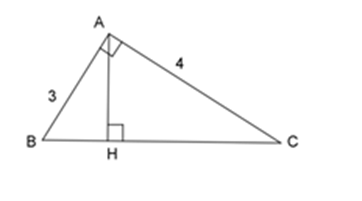
Áp dụng định lý Pytago vào tam giác vuông $ABC$ ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {3^2} + {4^2} = B{C^2}\\ \Leftrightarrow B{C^2} = 25\\ \Rightarrow BC = 5\;cm\end{array}\)
Xét 2 tam giác vuông $ABC$ và $HBA$ có: \(\widehat B\) chung
\( \Rightarrow \Delta ABC\backsim\Delta HBA\;(g - g)\)
\( \Rightarrow \dfrac{{AB}}{{HB}} = \dfrac{{BC}}{{BA}} \Rightarrow HB = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = 1,8\;cm\)
Mặt khác:
\(\dfrac{{AB}}{{HB}} = \dfrac{{AC}}{{HA}} \Rightarrow HA = \dfrac{{AC.HB}}{{AB}} = \dfrac{{4.1,8}}{3} = 2,4\;cm\)
Nên \(HA = 2,4\,cm;\,HB = 1,8\,cm\) .
Rút gọn biểu thức \(A = \left( {{x^2} + 2 - 2x} \right)\left( {{x^2} + 2 + 2x} \right) - {x^4}\) ta được kết quả là:
-
A.
\(A = 4\)
-
B.
$A = - 4$
-
C.
\(A = 19\)
-
D.
\(A = - 19\)
Đáp án : A
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Hoặc sử dụng hằng đẳng thức $(a+b)(a-b)=a^2-b^2$ và $(a+b)^2=a^2+2ab+b^2$
$A = \left( {{x^2} + 2 - 2x} \right)\left( {{x^2} + 2 + 2x} \right) - {x^4} $$= {x^2}.{x^2} + 2.{x^2} + 2x.{x^2} + 2.{x^2} + 2.2 + 2.2x - 2x.{x^2} - 2.2x - 2x.2x - {x^4} $$=x^4+2x^2+2x^3+2x^2+4+4x-2x^3-4x-4x^2-x^4$$= 4$
Vậy $A = 4$.
Biết \({x_0}\) là nghiệm nhỏ nhất của phương trình
\(\dfrac{1}{{{x^2} + 4x + 3}} + \dfrac{1}{{{x^2} + 8x + 15}} + \dfrac{1}{{{x^2} + 12x + 35}} + \dfrac{1}{{{x^2} + 16x + 63}} = \dfrac{1}{5}.\) Chọn khẳng định đúng .
-
A.
\({x_0} > 0\)
-
B.
\({x_0} < - 5\)
-
C.
\({x_0} = - 10\)
-
D.
\({x_0} > 5\)
Đáp án : B
Phân tích mẫu thức thành nhân tử rồi sử dụng phương pháp tách hạng tử để giải
\(\dfrac{1}{{\left( {x + a} \right)\left( {x + b} \right)}} = \dfrac{1}{{b - a}}\left( {\dfrac{1}{{x + a}} - \dfrac{1}{{x + b}}} \right),a \ne b\) .
Sau đó, làm theo các bước giải phương trình chứa ẩn ở mẫu:
+ Tìm ĐKXĐ của phương trình.
+ Quy đồng mẫu rồi khử mẫu.
+ Giải phương trình vừa nhận được.
+ Đối chiếu điều kiện rồi kết luận nghiệm.
Phân tích các mẫu thành nhân tử sau đó nhân cả 2 vế của phương trình với 2 ta được:
\(\dfrac{1}{{\left( {x + 1} \right)\left( {x + 3} \right)}} + \dfrac{1}{{\left( {x + 3} \right)\left( {x + 5} \right)}} + \dfrac{1}{{\left( {x + 5} \right)\left( {x + 7} \right)}} + \dfrac{1}{{\left( {x + 7} \right)\left( {x + 9} \right)}} = \dfrac{1}{5} \)
\(\dfrac{2}{{\left( {x + 1} \right)\left( {x + 3} \right)}} + \dfrac{2}{{\left( {x + 3} \right)\left( {x + 5} \right)}} + \dfrac{2}{{\left( {x + 5} \right)\left( {x + 7} \right)}} + \dfrac{2}{{\left( {x + 7} \right)\left( {x + 9} \right)}} = \dfrac{2}{5}\)
ĐKXĐ: $x \ne - 1; - 3; - 5; - 7; - 9$ .
Khi đó:
\( \dfrac{1}{{x + 1}} - \dfrac{1}{{x + 3}} + \dfrac{1}{{x + 3}} - \dfrac{1}{{x + 5}} + \dfrac{1}{{x + 5}} - \dfrac{1}{{x + 7}} + \dfrac{1}{{x + 7}} - \dfrac{1}{{x + 9}} = \dfrac{2}{5} \\\dfrac{1}{{x + 1}} - \dfrac{1}{{x + 9}} = \dfrac{2}{5} \\\dfrac{{1\left( {x + 9} \right) - 1\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x + 9} \right)}} = \dfrac{{2\left( {x + 1} \right)\left( {x + 9} \right)}}{{5\left( {x + 1} \right)\left( {x + 9} \right)}} \\5\left[ {x + 9 - \left( {x + 1} \right)} \right] = 2\left( {x + 1} \right)\left( {x + 9} \right)\\5\left( {x + 9 - x - 1} \right) = 2{x^2} + 20x + 18\\2{x^2} + 20x - 22 = 0\\{x^2} + 10x - 11 = 0\\{x^2} - x + 11x - 11 = 0 \\\left( {x - 1} \right)\left( {x + 11} \right) = 0\)
Suy ra \(x - 1 = 0\) hoặc \(x + 11 = 0\)
hay \(x = 1\left( {TM} \right)\) hoặc \(x = - 11 \left( {TM} \right)\)
Vậy \({x_0} = - 11 < - 5\) .
Cho hai điểm $A,B$ nằm trên cùng một nửa mặt phẳng bờ là đường thẳng $d$ . Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. Tìm trên đường thẳng $d$ điểm $M$ sao cho tổng $MA + MB$ nhỏ nhất. Chọn khẳng định đúng nhất.
-
A.
\(M\) là giao điểm của đoạn thẳng $AB$ và đường thẳng $d$.
-
B.
\(M\) là giao điểm của đoạn thẳng $AB'$ và đường thẳng $d$.
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai.
Đáp án : B
Ta nhân thấy nếu $A,{\rm{ }}B$ nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng $d$ thì tổng $MA + MB$ nhỏ nhất là đoạn $AB$ . Do vậy ta tìm cách đưa bài toán về trường hợp này.
Bằng cách dựng $B'$ đối xứng với $B$ qua $d$ ta đưa bài toán đã cho về trường hợp nêu trên vì $MB = MB'$ .
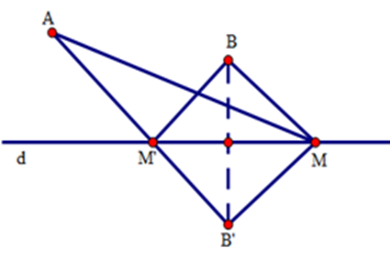
Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. $B'$ cố định.
Ta có $MB = MB'$ (tính chất đối xứng trục).
Xét ba điểm $M,{\rm{ }}A,{\rm{ }}B'$ ta có $MA + MB' \ge AB'$
Do đó $MA + MB \ge AB'$
Dấu “=” xảy ra khi và chỉ khi $A,M,B'$ thẳng hàng theo thứ tự đó hay $M$ là giao điểm của đoạn $AB'$ và đường thẳng $d$ .
Vậy khi \(M \equiv M'\) là giao điểm của đoạn thẳng $AB'$ và đường thẳng $d$ thì tổng $MA + MB$ nhỏ nhất, trong đó $B'$ là điểm đối xứng của $B$ qua $d$ .
Tính \(x,y\) trên hình vẽ, trong đó \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\). Hãy chọn câu đúng.

-
A.
\(x = 8cm,y = 16cm\).
-
B.
\(x = 18cm,y = 9cm\).
-
C.
\(x = 18cm,y = 8cm\).
-
D.
\(x = 16cm,y = 8cm\).
Đáp án : D
Ta sử dụng định lý đường trung bình của hình thang để tính độ dài $x;\,y$.
+ Vì \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\) nên các tứ giác \(EFCD;\,ABHG\) là hình thang.
+ Từ hình vẽ ta có \(GH\) là đường trung bình của hình thang \(EFCD \Rightarrow HG = \dfrac{{EF + CD}}{2}\) \( = \dfrac{{12 + 20}}{2} = 16\,cm\) .
Hay \(x = 16\,cm\) .
+ Lại có \(EF\) là đường trung bình của hình thang \(ABHG \Rightarrow EF = \dfrac{{AB + HG}}{2}\)
\( \Rightarrow 12 = \dfrac{{AB + 16}}{2} \Rightarrow AB + 16 = 24 \Rightarrow AB = 8\,cm\) hay \(y = 8\,cm\) .
Vậy \(x = 16\,cm;\,y = 8\,cm\) .
Cho hình thang $ABCD\left( {AB{\rm{//}}CD} \right),$ đường cao $AH$, \(AB = 4\,cm,CD = 8\,cm,\) diện tích hình thang là \(54\,c{m^2}\) thì $AH$ bằng
-
A.
\(5\,cm\)
-
B.
\(4\,cm\)
-
C.
\(4,5\,cm\)
-
D.
\(9\,cm\)
Đáp án : D
Từ công thức tính diện tích hình thang suy ra cách tính đường cao.
\({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2} \Rightarrow AH = \dfrac{{2{S_{ABCD}}}}{{AB + CD}} = \dfrac{{2.54}}{{4 + 8}} = 9\,(cm)\)
Số đo mỗi góc trong và ngoài của ngũ giác đều là:
-
A.
\(75^\circ ;150^\circ \)
-
B.
\(108^\circ ;72^\circ \)
-
C.
\(100^\circ ;80^\circ \)
-
D.
\(110^\circ ;70^\circ \)
Đáp án : B
Số đo góc của hình n giác đều: \(\dfrac{{\left( {n - 2} \right){{.180}^0}}}{n}\) (với $n \ge 3$).
Góc trong và góc ngoài n giác đều kề bù.
Số đo góc trong của hình ngũ giác đều: \(\dfrac{{\left( {5 - 2} \right){{.180}^0}}}{5} = 108^\circ \)
Vì góc trong và ngóc ngoài đa giác kề bù nên số đo góc ngoài ngũ giác đều là: \(180^\circ - 108^\circ = 72^\circ \)
Một ô tô phải đi quãng đường $AB$ dài $60$ km trong một thời gian nhất định. Xe đi nửa đầu quãng đường với vận tốc hơn dự định $10$ km/h và đi với nửa sau kém hơn dự định $6$ km/h. Biết ô tô đến đúng dự định. Tính thời gian dự định đi quãng đường $AB$ ?
-
A.
\(3\) giờ
-
B.
\(6\) giờ
-
C.
\(5\) giờ
-
D.
\(2\) giờ
Đáp án : D
Giải bài toán chuyển động bằng cách lập phương trình.
+) Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
+) Sau đó dựa vào giả thiết của đề bài để lập phương trình.
+) Giải phương trình rồi so sánh điều kiện để kết luận.
Gọi vận tốc theo dự định của ô tô là \(x\,\left( {x > 6} \right)\)(km/h)
Thời gian theo dự định của ô tô là \(\dfrac{{60}}{x}\left( h \right)\)
Nửa đầu quãng đường ô tô đi với vận tốc là \(x + 10\) (km/h)
Thời gian đi nửa đầu quãng đường là \(\dfrac{{30}}{{x + 10}}\,\left( h \right)\)
Nửa sau quãng đường, ô tô đi với vận tốc là \(x - 6\,\) (km/h)
Thời gian ô tô đi nửa sau quãng đường là \(\dfrac{{30}}{{x - 6}}\,\left( h \right)\)
Vì ô tô đến nơi đúng dự định nên ta có phương trình
\(\dfrac{{30}}{{x + 10}} + \dfrac{{30}}{{x - 6}} = \dfrac{{60}}{x}\)\( \Leftrightarrow \dfrac{{30x\left( {x - 6} \right) + 30x\left( {x + 10} \right)}}{{x\left( {x + 10} \right)\left( {x - 6} \right)}} = \dfrac{{60\left( {x - 6} \right)\left( {x + 10} \right)}}{{x\left( {x + 10} \right)\left( {x - 6} \right)}}\)
\( \Rightarrow {x^2} - 6x + {x^2} + 10x = 2\left( {{x^2} + 4x - 60} \right)\)\( \Leftrightarrow 4x = 120\, \Leftrightarrow x = 30\,\left( {TM} \right)\)
Vậy thời gian dự định đi quãng đường \(AB\) là \(60:30 = 2\) giờ.
Cho \(a + 8 < b\). So sánh \(a - 7\) và \(b - 15\)
-
A.
\(a - 7 < b - 15\)
-
B.
\(a - 7 > b - 15\)
-
C.
\(a - 7 \ge b - 15\)
-
D.
\(a - 7 \le b - 15\)
Đáp án : A
Sử dụng tính chất: Cộng cả hai vế với một số thì dấu không đổi để làm xuất hiện \(a - 7\) và \(b - 15\)
Cộng cả hai vế của bất đẳng thức \(a + 8 < b\) với $\left( { - 15} \right)$ ta được
\(a + 8 < b \)
\(a + 8 - 15 < b - 15 \)
\(a - 7 < b - 15\)
Tập nghiệm của bất phương trình \(\left| {1 - x} \right| \ge 3\) là
-
A.
\(x \ge 4,x \le - 2\)
-
B.
\( - 2 \le x \le 4\)
-
C.
\(x \le - 2,x \le 4\)
-
D.
\(x \le 4,x \ge - 2\)
Đáp án : A
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\)
+ Giải các bất phương trình bậc nhất một ẩn
+ Kết hợp với điều kiện và kết luận.
TH1: \(\left| {1 - x} \right| = 1 - x\) với \(1 - x \ge 0 \Leftrightarrow x \le 1\)
Bất phương trình đã cho trở thành \(1 - x \ge 3 \Leftrightarrow x \le - 2\), kết hợp điều kiện \(x \le 1\) ta có \(x \le - 2\).
TH2: \(\left| {1 - x} \right| = x - 1\) với \(1 - x < 0 \Leftrightarrow x > 1\)
Bất phương trình đã cho trở thành \(x - 1 \ge 3 \Leftrightarrow x \ge 4\), kết hợp điều kiện \(x > 1\) ta có \(x \ge 4\).
Vậy bất phương trình có nghiệm \(x \ge 4,x \le - 2\)
Hãy chọn câu đúng ?
Cho tam giác \(ABC\) có chu vi là \(32\) cm. Gọi \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\). Chu vi của tam giác \(EFP\) là
-
A.
\(17\,cm\).
-
B.
\(33\,cm\).
-
C.
\(15\,cm\).
-
D.
\(16\,cm\).
Đáp án : D
Ta sử dụng định lý đường trung bình của tam giác để tìm mối liên hệ giữa chu vi tam giác \(ABC\) và chu vi tam giác \(EFP\) .
Vì \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\) nên \(EF;EP;FP\) là các đường trung bình của tam giác \(ABC\) .
Suy ra \(EF = \dfrac{1}{2}AC;\,FP = \dfrac{1}{2}AB;\,EP = \dfrac{1}{2}BC\) \( \Rightarrow EF + FP + EP = \dfrac{1}{2}AC + \dfrac{1}{2}AB + \dfrac{1}{2}BC\)
\( \Leftrightarrow EF + FP + EP = \dfrac{1}{2}\left( {AB + AC + BC} \right)\) hay chu vi tam giác \(EFP = \dfrac{1}{2}\) chu vi tam giác \(ABC\) .
Do đó chu vi tam giác \(EFP\) là \(32:2 = 16\) cm .
Tìm giá trị nguyên của \(x\) để phân thức \(\dfrac{3}{{x + 2}}\) có giá trị là một số nguyên.
-
A.
$x = - 3$
-
B.
\(x \in \left\{ { - 1;1} \right\}\)
-
C.
\(x \in \left\{ { - 1;1; - 5; - 3} \right\}\)
-
D.
$x = - 1$
Đáp án : C
Bước 1: Tìm điều kiện xác định.
Bước 2: Phân thức \(\dfrac{A}{B}\) đạt giá trị nguyên khi \(A \vdots B\) , từ đó tìm được \(x\) .
Bước 3: So sánh với điều kiện để kết luận các giá trị thỏa mãn.
Điều kiện: \(x + 2 \ne 0 \Leftrightarrow x \ne - 2\) .
Ta có \(\dfrac{3}{{x + 2}} \in \mathbb{Z} \Rightarrow x + 2 \in \)Ư\(\left( 3 \right)\) \( = \left\{ { - 1;1; - 3;3} \right\}\) .
+ $x + 2 = - 1 \Leftrightarrow x = - 3\,\,\left( {TM} \right)$
+ \(x + 2 = 1 \Leftrightarrow x = - 1\,\,\left( {TM} \right)\)
+ \(x + 2 = - 3 \Leftrightarrow x = - 5\,\left( {TM} \right)\)
+ $x + 2 = 3 \Leftrightarrow x = 1\,\,\left( {TM} \right)$
Vậy \(x \in \left\{ { - 1;1; - 5; - 3} \right\}\) .
Kết quả của phép chia \(\dfrac{{5\left( {x + 1} \right)}}{{x{y^2}}}:\dfrac{{10\left( {x + 1} \right)}}{{3{x^2}y}}\) là
-
A.
\(\dfrac{{50{{\left( {x + 1} \right)}^2}}}{{3{x^3}{y^3}}}\) .
-
B.
\(\dfrac{{3{x^2}}}{{2y}}\).
-
C.
\(\dfrac{{3x}}{{2y}}\).
-
D.
\(\dfrac{{3x}}{{2{y^2}}}\).
Đáp án : C
Bước 1: Thực hiện phép chia hai phân thức: \(\dfrac{A}{B}:\dfrac{C}{D} = \dfrac{A}{B}.\dfrac{D}{C};\,\,\left( {\dfrac{C}{D} \ne 0} \right)\)
Bước 2: Rút gọn phân thức thu được.
Ta có \(\dfrac{{5\left( {x + 1} \right)}}{{x{y^2}}}:\dfrac{{10\left( {x + 1} \right)}}{{3{x^2}y}}\)\( = \dfrac{{5\left( {x + 1} \right)}}{{x{y^2}}}.\dfrac{{3{x^2}y}}{{10\left( {x + 1} \right)}} = \dfrac{{15\left( {x + 1} \right){x^2}y}}{{10\left( {x + 1} \right)x{y^2}}} = \dfrac{{3x}}{{2y}}\) .
Thu gọn \(6{x^4}{y^2}:{\left( {\dfrac{1}{2}{x^2}y} \right)^2}\), ta được
-
A.
$12$
-
B.
$24$
-
C.
$24{x^2}y$
-
D.
$12{x^2}y$
Đáp án : B
Sử dụng các công thức lũy thừa của một tích\({\left( {x.y} \right)^m} = {x^m}.{y^m}\)và thương các lũy thừa\({x^m}:{x^n} = {x^{m - n}}\,\,\left( {m \ge n,\,m,\,n \in \mathbb{N}} \right)\)
Ta có \(6{x^4}{y^2}:{\left( {\dfrac{1}{2}{x^2}y} \right)^2} \)\(= 6{x^4}{y^2}:\left[ {\dfrac{1}{4}{{\left( {{x^2}} \right)}^2}.{y^2}} \right] \)\(= 6{x^4}{y^2}:\left( {\dfrac{1}{4}{x^4}{y^2}} \right) \)\(= 6:\dfrac{1}{4} = 24\)
Giá trị của biểu thức \(P = - 2{x^2}y\left( {xy + {y^2}} \right)\) tại \(x = - 1;\,y = 2\) là
-
A.
$8$
-
B.
$ - 8$
-
C.
$6$
-
D.
$ - 6$
Đáp án : B
Nhân đơn thức với đa thức
Thay \({x_0};{y_0}\) biểu thức trên rồi thực hiện phép tính.
Ta có:
\(P = - 2{x^2}y\left( {xy + {y^2}} \right)\)
\(P = - 2{x^3}{y^2} - 2{x^2}{y^3}\)
Thay \(x = - 1;y = 2\) vào biểu thức ta được
\(\begin{array}{l}P = - 2{\left( { - 1} \right)^3}{.2^2} - 2.{\left( { - 1} \right)^2}{.2^3}\\P = 8 - 16 = - 8\end{array}\)
Vậy \(P = - 8\) .
Cho hai số tự nhiên \(n\) và \(m\). Biết rằng \(n\) chia \(5\) dư \(1\), \(m\) chia \(5\) dư \(4\). Hãy chọn câu đúng:
-
A.
\(m.n\) chia \(5\) dư \(1\)
-
B.
\(m - n\) chia hết cho \(5\)
-
C.
\(m + n\) chia hết cho \(5\)
-
D.
\(m.n\) chia \(5\) dư \(3\)
Đáp án : C
- Biểu diễn \(m\) và \(n\) theo giả thiết
- Tính \(m.n,\,m + n,\,m - n\) rồi đánh giá tinh chia hết của từng biểu thức
Ta có $n$ chia \(5\) dư \(1\) nên \(n = 5p + 1\,\left( {0 < p < n;p \in \mathbb{N}} \right)\) ; \(m\) chia \(5\) dư \(4\) nên \(m = 5q + 4\,\left( {0 < q < m;q \in \mathbb{N}} \right)\)
Khi đó \(m.n = \left( {5p + 1} \right)\left( {5q + 4} \right) = 25pq + 20p + 5q + 4 = 5\left( {5pq + 4p + q} \right) + 4\) mà \(5\left( {5pq + 4p + q} \right) \vdots \,5\) nên \(m.n\) chia $5$ dư \(4\) , phương án A sai, D sai.
Ta có \(m - n = 5q + 4 - \left( {5p + 1} \right) = 5q - 5p + 3\) mà $5p \vdots 5;\,\,5q \vdots 5$ nên \(m - n\) chia \(5\) dư \(3\) , phương án B sai.
Ta có \(m + n = 5q + 4 + 5p + 1 = 5q + 5p + 5 = 5\left( {q + p + 1} \right) \vdots 5\) nên C đúng.
Phân tích đa thức \({x^3} + 12x\) thành nhân tử ta được
-
A.
\({x^2}\left( {x + 12} \right)\).
-
B.
\(x\left( {{x^2} + 12} \right)\).
-
C.
\(x\left( {{x^2} - 12} \right)\).
-
D.
\({x^2}\left( {x - 12} \right)\).
Đáp án : B
Ta có \({x^3} + 12x\)\( = x.{x^2} + x.12 = x\left( {{x^2} + 12} \right)\)
Cho \(x + n = 2\left( {y - m} \right),\)
khi đó giá trị của biểu thức \(A = {x^2} - 4xy + 4{y^2} - 4{m^2} - 4mn - {n^2}\) bằng
-
A.
\(A = 1\).
-
B.
\(A = 0\).
-
C.
\(A = 2\).
-
D.
Chưa đủ dữ kiện để tính.
Đáp án : B
+ Sử dụng các hằng đẳng thức \({A^2} - 2AB + {B^2} = {\left( {A - B} \right)^2}\); \({A^2} + 2AB + {B^2} = {\left( {A + B} \right)^2}\)để biến đổi.
+ Sử dụng hằng đẳng thức \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\) để phân tích đa thức thành nhân tử.
+ Sử dụng giả thiết \(x + n = 2\left( {y - m} \right)\) để tính giá trị biểu thức.
Ta có \(A = {x^2} - 4xy + 4{y^2} - 4{m^2} - 4mn - {n^2}\)\( = {x^2} - 2x.2y + {\left( {2y} \right)^2} - \left( {4{m^2} + 4mn + {n^2}} \right)\)
\( = {\left( {x - 2y} \right)^2} - {\left( {2m + n} \right)^2}\)\( = \left( {x - 2y + 2m + n} \right)\left( {x - 2y - 2m - n} \right)\)
Ta có \(x + n = 2\left( {y - m} \right) \)\(\Leftrightarrow x + n = 2y - 2m \)\(\Leftrightarrow x - 2y + n + 2m = 0\)
Thay \(x - 2y + n + 2m = 0\) vào \(A\) ta được \(A = 0.\left( {x - 2y - 2m - n} \right) = 0\) .
Vậy \(A = 0\) .