Đề thi khảo sát chất lượng đầu năm Toán 9 - Đề số 9
Đề bài
Cho tam giác \(ABC\) có \(BC = 6cm.\) Trên cạnh \(AB\) lấy các điểm \(D\) và \(E\) sao cho \(AD = BE.\) Qua \(D,E\) lần lượt vẽ các đường thẳng song song với \(BC,\) cắt \(AC\) theo thứ tự ở \(G\) và \(H\). Tính tổng \(DG + EH.\)
-
A.
\(10\,cm\)
-
B.
\(4\,cm\)
-
C.
\(6\,cm\)
-
D.
\(8\,cm\)
Cho \( - 2018a < - 2018b\). Khi đó
-
A.
\(a < b\)
-
B.
\(a > b\)
-
C.
\(a = b\)
-
D.
Cả A, B, C đều sai
Trong tháng Giêng hai tổ công nhân may được $800$ chiếc áo. Tháng Hai, tổ $1$ vượt mức $15\% $ , tổ hai vượt mức $20\% $ do đó cả hai tổ sản xuất được $945$ cái áo. Tính xem trong tháng đầu, tổ \(1\) may được bao nhiêu chiếc áo?
-
A.
\(300\)
-
B.
\(500\)
-
C.
\(400\)
-
D.
\(600\)
Một người đi xe máy từ $A$ đến $B$ , với vận tốc $30$ km/h. Lúc về người đó đi với vận tốc $24$ km/h. Do đó thời gian về lâu hơn thời gian đi là $30$ phút. Hãy chọn câu đúng: Nếu gọi quãng đường $AB$ là \(x\) (km,\(x > 0\)) thì phương trình của bài toán là:
-
A.
\(\dfrac{x}{{24}} + \dfrac{x}{{30}} = \dfrac{1}{2}\).
-
B.
\(\dfrac{x}{{24}} - \dfrac{x}{{30}} = - \dfrac{1}{2}\).
-
C.
\(\dfrac{x}{{24}} - \dfrac{x}{{30}} = \dfrac{1}{2}\) .
-
D.
\(\dfrac{x}{{30}} - \dfrac{x}{{24}} = \dfrac{1}{2}\).
Với điều kiện nào của $x$ thì hai phân thức \(\dfrac{{x - 2}}{{{x^2} - 5x+ 6}}\) và \(\dfrac{1}{{x - 3}}\) bằng nhau.
-
A.
\(x = 3\)
-
B.
\(x \ne 3\)
-
C.
\(x \ne 2\)
-
D.
\(\left\{ \begin{array}{l}x \ne 2\\x \ne 3\end{array} \right.\)
Gọi \({x_1};{x_2}\) là hai giá trị thỏa mãn \(3{x^2} + 13x + 10 = 0\). Khi đó \(2{x_1}.{x_2}\) bằng
-
A.
\( - \dfrac{{20}}{3}\).
-
B.
\(\dfrac{{20}}{3}\).
-
C.
\(\dfrac{{10}}{3}\).
-
D.
\( - \dfrac{{10}}{3}\).
Cho phương trình: \(\left( {{m^2} - 3m + 2} \right)x = m - 2\) , với $m$ là tham số. Tìm \(m\) để phương trình vô số nghiệm.
-
A.
$m=1$
-
B.
$m = 2$
-
C.
$m=0$
-
D.
$m\in \{1;2\}$
Phép tính \(\dfrac{{24x{y^2}{z^2}}}{{12{x^2}z}}.\dfrac{{4{x^2}y}}{{6x{y^4}}}\) có kết quả là
-
A.
\(\dfrac{{24z}}{{18y}}\) .
-
B.
\(\dfrac{{24xz}}{{18xy}}\).
-
C.
\(\dfrac{{4x}}{{3y}}\).
-
D.
\(\dfrac{{4z}}{{3y}}\).
Dao động điện từ trong mạch LC tắt càng nhanh khi ?
-
A.
Tụ điện có điện dung càng lớn.
-
B.
Mạch có điện trở càng lớn.
-
C.
Mạch có tần số riêng càng lớn.
-
D.
Cuộn dây có độ tự cảm càng lớn.
Cho biết \(3{y^2} - 3y\left( {y - 2} \right) = 36\). Giá trị của $y$ là:
-
A.
5
-
B.
6
-
C.
7
-
D.
8
Cho hình bình hành $ABCD$ , $O$ là giao điểm của hai đường chéo. Một đường thẳng đi qua $O$ cắt các cạnh $AB$ và $CD$ theo thứ tự ở $M$ và $N$ . Chọn khẳng định đúng .
-
A.
Điểm $M$ đối xứng với điểm $N$ qua$O$ .
-
B.
Điểm $M$ đối xứng với điểm $O$ qua$N$.
-
C.
Điểm $N$ đối xứng với điểm $O$ qua$M$.
-
D.
Điểm $A$ đối xứng với điểm $B$ qua$M$.
Bất phương trình $2{(x + 2)^2} < 2x(x + 2) + 4$ có nghiệm là
-
A.
$x > - 1$
-
B.
$x > 1$
-
C.
$x \ge - 1$
-
D.
$x < - 1$
Tính thể tích của hình chóp tam giác đều có tất cả các cạnh đều bằng $6\,cm$ (làm tròn đến chữ số thập phân thứ hai).
-
A.
\(24,64\,c{m^3}\)
-
B.
\(25,46\,c{m^3}\)
-
C.
\(26,46\,c{m^3}\)
-
D.
\(26,64\,c{m^3}\)
Hình chữ nhật có chiều dài giảm đi $5$ lần và chiều rộng tăng lên \(5\) lần, khi đó diện tích của hình chữ nhật
-
A.
Không thay đổi.
-
B.
Tăng \(5\) lần.
-
C.
Giảm \(5\) lần.
-
D.
Giảm \(3\) lần.
Cho tam giác $ABC$ có $AB = 9\,cm,AC = 16\,cm,BC = 20\,cm$ . Khi đó
-
A.
\(\widehat B = \widehat {\dfrac{A}{3}}\)
-
B.
\(\widehat B = \dfrac{2}{3}\widehat A\)
-
C.
\(\widehat B = \widehat {\dfrac{A}{2}}\)
-
D.
\(\widehat B = \widehat C\)
Cho hình thang $ABCD{\rm{ }},{\rm{ }}AB$ song song với $CD,$ đường cao $AH.$ Biết \(AB = 7cm;\,CD = 10cm\) , diện tích của $ABCD$ là \(25,5c{m^2}\) thì độ dài $AH$ là:
-
A.
2,5cm
-
B.
3cm
-
C.
3,5cm
-
D.
5cm
Tập nghiệm của phương trình \(\dfrac{{ - 7{x^2} + 4}}{{{x^3} + 1}} = \dfrac{5}{{{x^2} - x + 1}} - \dfrac{1}{{x + 1}}\) là
-
A.
\(S = \left\{ {0;1} \right\}\)
-
B.
\(S = \left\{ { - 1} \right\}\)
-
C.
\(S = \left\{ {0; - 1} \right\}\)
-
D.
\(S = \left\{ 0 \right\}\)
Phương trình \({x^2} + x = 0\) có số nghiệm là
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
vô nghiệm
-
D.
vô số nghiệm
Giá trị lớn nhất của phân thức $\dfrac{5}{{{x^2} - 6x + 10}}$ là :
-
A.
$5$
-
B.
$ - 5$
-
C.
$2$
-
D.
$ - 2$
Tìm \(y\) trong hình vẽ dưới đây.
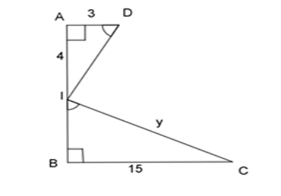
-
A.
\(17,85\)
-
B.
\(10,75\)
-
C.
\(18,75\)
-
D.
\(15,87\)
Cho biết \(\dfrac{{AB}}{{CD}} = \dfrac{5}{7}\) và đoạn thẳng $AB$ ngắn hơn đoạn thẳng $CD$ là $10{\rm{ }}cm.$ Tính độ dài các đoạn thẳng$AB,{\rm{ }}CD$ ?
-
A.
$AB = 35{\rm{ }}cm,{\rm{ }}CD = 25{\rm{ }}cm$
-
B.
$AB = 20{\rm{ }}cm,{\rm{ }}CD = 30{\rm{ }}cm$
-
C.
$AB = 25{\rm{ }}cm,{\rm{ }}CD = 35{\rm{ }}cm$
-
D.
$AB = 30{\rm{ }}cm,{\rm{ }}CD = 20{\rm{ }}cm$
Số nguyên nhỏ nhất thỏa mãn bất phương trình $x(5x + 1) + 4(x + 3) > 5{x^2}$ là
-
A.
$x = - 3$
-
B.
$x = 0$
-
C.
\(x = - 1\)
-
D.
\(x = - 2\).
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
-
A.
\( - 16\)
-
B.
\( - 8\)
-
C.
\(16\)
-
D.
\(8\).
Cho tam giác ABC, M thuộc cạnh AB, N thuộc cạnh BC, biết \(\frac{{MA}}{{MB}} = \frac{{NC}}{{NB}} = \frac{2}{5},MN = 15\left( {cm} \right)\). Tính độ dài cạnh AC.
-
A.
AC = 21 (cm).
-
B.
AC = 37,5 (cm)
-
C.
AC = 52,5 (cm).
-
D.
AC = 25 (cm).
Cho đa thức \(F\left( x \right) = a{x^2} + bx + c\) với các hệ số \(a,\,b,\,c\) thỏa mãn \(11a - b + 5c = 0\).
Chọn câu đúng.
-
A.
\(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) cùng dấu dương
-
B.
\(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) cùng dấu âm
-
C.
\(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) có thể cùng dấu hoặc trái dấu
-
D.
\(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) luôn trái dấu
Có bao nhiêu nghiệm của đa thức \(2{x^2} + 7x - 9\)?
-
A.
\(3\)
-
B.
\(0\)
-
C.
\(1\)
-
D.
\(2\)
Cho \(\Delta ABC\) có \(AB = AC\), \(\widehat A = 2\widehat B\) có dạng đặc biệt nào:
-
A.
Tam giác vuông
-
B.
Tam giác đều
-
C.
Tam giác cân
-
D.
Tam giác vuông cân
Cho \(B = \dfrac{{x - 1}}{{x - 2}}\). Số giá trị của \(x \in Z\) để \(B \in \mathbb{Z}\) là:
-
A.
3
-
B.
0
-
C.
2
-
D.
-2
Lời giải và đáp án
Cho tam giác \(ABC\) có \(BC = 6cm.\) Trên cạnh \(AB\) lấy các điểm \(D\) và \(E\) sao cho \(AD = BE.\) Qua \(D,E\) lần lượt vẽ các đường thẳng song song với \(BC,\) cắt \(AC\) theo thứ tự ở \(G\) và \(H\). Tính tổng \(DG + EH.\)
-
A.
\(10\,cm\)
-
B.
\(4\,cm\)
-
C.
\(6\,cm\)
-
D.
\(8\,cm\)
Đáp án : C
+ Kẻ \(HM//AB\,\,\left( {M \in BC} \right)\).
+ Chứng minh \(DG = MC\) từ hai tam giác bằng nhau từ đó tính tổng \(DG + EH\).
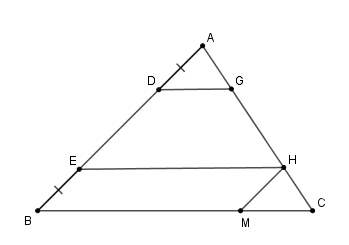
Kẻ \(HM//AB\,\,\left( {M \in BC} \right)\).
Xét tứ giác \(EHMB\) có \(MH//EB;EH//BM\) nên \(EHMB\) là hình bình hành.
Suy ra \(EH = BM;\,EB = HM\) (tính chất hình bình hành) mà \(AD = BE \Rightarrow AD = MH\).
Lại có: \(DG//BC \Rightarrow \widehat {ADG} = \widehat {ABC}\) (hai góc ở vị trí đồng vị) (1)
Và \(HM//AB \Rightarrow \widehat {HMC} = \widehat {ABC}\) và \(\widehat {CHM} = \widehat {CAB}\) (hai góc ở vị trí đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {HMC} = \widehat {ADG}\left( { = \widehat {ABC}} \right)\).
Xét \(\Delta ADG\) và \(\Delta HMC\) có: \(\left\{ \begin{array}{l}\widehat {MHC} = \widehat {DAG}\left( {cmt} \right)\\AD = HM\,\left( {cmt} \right)\\\widehat {HMC} = \widehat {ADG}\left( {cmt} \right)\end{array} \right.\) nên \(\Delta ADG = \Delta HMC\left( {g - c - g} \right) \Rightarrow DG = MC\).
Ta có: \(DG + EH = MC + BM = BC = 6cm\).
Cho \( - 2018a < - 2018b\). Khi đó
-
A.
\(a < b\)
-
B.
\(a > b\)
-
C.
\(a = b\)
-
D.
Cả A, B, C đều sai
Đáp án : B
Ta có \( - 2018a < - 2018b\)
Nhân cả hai vế với \(- \dfrac{1}{{2018}}\) ta được
\( - 2018.\left( { - \dfrac{1}{{2018}}} \right)a > - 2018.\left( { - \dfrac{1}{{2018}}} \right)b \)
hay \( a > b\) .
Trong tháng Giêng hai tổ công nhân may được $800$ chiếc áo. Tháng Hai, tổ $1$ vượt mức $15\% $ , tổ hai vượt mức $20\% $ do đó cả hai tổ sản xuất được $945$ cái áo. Tính xem trong tháng đầu, tổ \(1\) may được bao nhiêu chiếc áo?
-
A.
\(300\)
-
B.
\(500\)
-
C.
\(400\)
-
D.
\(600\)
Đáp án : A
Giải theo các bước sau:
+ Lập phương trình: Chọn ẩn và đặt điều kiện; biểu diễn đại lượng chưa biết theo ẩn và đại lượng đã biết; lập Phương trình biểu thị mối quan hệ giữa các đại lượng
+ Giải phương trình
+ Đối chiếu điều kiện rồi kết luận
Gọi số áo tổ \(1\) làm được trong tháng Giêng là \(x\,\left( {x \in \mathbb{N}*;\,x < 800} \right)\)(áo)
Thì số áo tổ \(2\) làm được trong tháng Giêng là \(800 - x\) (áo)
Vì tháng hai, tổ \(1\) vượt mức $15\% $ nên số áo vượt mức là \(15\% .x = \dfrac{3}{{20}}x\) (áo)
Và tổ \(2\) vượt mức \(20\% \) nên số áo vượt mức là \(20\% \left( {800 - x} \right) = \dfrac{{800 - x}}{5}\) (áo)
Vì tháng hai, cả hai tổ sản xuất được $945$ cái áo nên vượt mức với tháng Giêng là \(945 - 800 = 145\) áo
Nên ta có phương trình \(\dfrac{3}{{20}}x + \dfrac{{800 - x}}{5} = 145 \Leftrightarrow 3x + 3200 - 4x = 2900 \Leftrightarrow x = 300\,\left( {TM} \right)\) .
Vậy trong tháng Giêng tổ một làm được \(300\) áo.
Một người đi xe máy từ $A$ đến $B$ , với vận tốc $30$ km/h. Lúc về người đó đi với vận tốc $24$ km/h. Do đó thời gian về lâu hơn thời gian đi là $30$ phút. Hãy chọn câu đúng: Nếu gọi quãng đường $AB$ là \(x\) (km,\(x > 0\)) thì phương trình của bài toán là:
-
A.
\(\dfrac{x}{{24}} + \dfrac{x}{{30}} = \dfrac{1}{2}\).
-
B.
\(\dfrac{x}{{24}} - \dfrac{x}{{30}} = - \dfrac{1}{2}\).
-
C.
\(\dfrac{x}{{24}} - \dfrac{x}{{30}} = \dfrac{1}{2}\) .
-
D.
\(\dfrac{x}{{30}} - \dfrac{x}{{24}} = \dfrac{1}{2}\).
Đáp án : C
+) Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
+) Sau đó dựa vào giả thiết của đề bài để lập phương trình.
Đổi: $30$ phút \( = \dfrac{{30}}{{60}} = \dfrac{1}{2}\,\,\left( h \right).\)
Với quãng đường AB là $x$ (km), thời gian người đó đi hết quãng đường lúc đi là: \(\dfrac{x}{{30}}\,\,\,\left( h \right);\) thời gian người đó đi quãng đường AB lúc về là: \(\dfrac{x}{{24}}\,\,\left( h \right).\)
Theo đề bài ta có phương trình: \(\dfrac{x}{{24}} - \dfrac{x}{{30}} = \dfrac{1}{2}\)
Với điều kiện nào của $x$ thì hai phân thức \(\dfrac{{x - 2}}{{{x^2} - 5x+ 6}}\) và \(\dfrac{1}{{x - 3}}\) bằng nhau.
-
A.
\(x = 3\)
-
B.
\(x \ne 3\)
-
C.
\(x \ne 2\)
-
D.
\(\left\{ \begin{array}{l}x \ne 2\\x \ne 3\end{array} \right.\)
Đáp án : D
Bước 1: Tìm điều kiện để phân thức xác định: \(B \ne 0\)
Bước 2: \(\dfrac{A}{B} = \dfrac{C}{D}\) nếu$A.D = B.C$ . Từ đó tìm được \(x\) .
Bước 3: So sánh với điều kiện ở bước 1 để kết luận.
Điều kiện: \(\left\{ \begin{array}{l}{x^2} - 5x + 6 \ne 0\\x - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right)\left( {x - 3} \right) \ne 0\\x - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2 \ne 0\\x - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne 3\end{array} \right.\) .
Ta có \(\dfrac{{x - 2}}{{{x^2} - 5{\rm{x}} + 6}} = \dfrac{1}{{x - 3}} \Leftrightarrow \dfrac{{x - 2}}{{\left( {x - 2} \right)\left( {x - 3} \right)}} = \dfrac{1}{{x - 3}}\)\( \Leftrightarrow \dfrac{{\left( {x - 2} \right):\left( {x - 2} \right)}}{{\left( {x - 3} \right)\left( {x - 2} \right):\left( {x - 2} \right)}} = \dfrac{1}{{\left( {x - 3} \right)}} \Leftrightarrow \dfrac{1}{{x - 3}} = \dfrac{1}{{x - 3}}\) (luôn đúng)
Nên hai phân thức trên bằng nhau khi \(\left\{ \begin{array}{l}x \ne 2\\x \ne 3\end{array} \right.\).
Gọi \({x_1};{x_2}\) là hai giá trị thỏa mãn \(3{x^2} + 13x + 10 = 0\). Khi đó \(2{x_1}.{x_2}\) bằng
-
A.
\( - \dfrac{{20}}{3}\).
-
B.
\(\dfrac{{20}}{3}\).
-
C.
\(\dfrac{{10}}{3}\).
-
D.
\( - \dfrac{{10}}{3}\).
Đáp án : B
Sử dụng phương pháp tách một hạng tử thành nhiều hạng tử để phân tích đa thức thành nhân tử.
Từ đó đưa về dạng tìm \(x\) đã biết \(A.B = 0 \Leftrightarrow \left[ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
Ta có \(3{x^2} + 13x + 10 = 0\)\( \Leftrightarrow 3{x^2} + 3x + 10x + 10 = 0 \Leftrightarrow 3x\left( {x + 1} \right) + 10\left( {x + 1} \right) = 0\)\( \Leftrightarrow \left( {x + 1} \right)\left( {3x + 10} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\3x + 10 = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - \dfrac{{10}}{3}\end{array} \right.\)
\( \Rightarrow 2{x_1}{x_2} = 2.\left( { - 1} \right).\left( { - \dfrac{{10}}{3}} \right) = \dfrac{{20}}{3}\) .
Cho phương trình: \(\left( {{m^2} - 3m + 2} \right)x = m - 2\) , với $m$ là tham số. Tìm \(m\) để phương trình vô số nghiệm.
-
A.
$m=1$
-
B.
$m = 2$
-
C.
$m=0$
-
D.
$m\in \{1;2\}$
Đáp án : B
Cho phương trình \(ax + b = 0\) \(\left( 1 \right)\) .
+ Nếu \(\left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\) thì phương trình \(\left( 1 \right)\) có vô số nghiệm.
\(\left( {{m^2} - 3m + 2} \right)x = m - 2(*)\)
Xét \({m^2} - 3m + 2 = 0\)\( \Leftrightarrow {m^2} - m - 2m + 2 = 0 \)\( \Leftrightarrow m\left( {m - 1} \right) - 2\left( {m - 1} \right) = 0\)\( \Leftrightarrow \left( {m - 1} \right)\left( {m - 2} \right) = 0 \)\( \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m - 2 = 0\end{array} \right. \)\( \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\)
+ Nếu \(m = 1 \Rightarrow \left( * \right) \Leftrightarrow 0x = 1\). Điều này vô lí. Suy ra phương trình (*) vô nghiệm.
+ Nếu \(m = 2 \Rightarrow \left( * \right) \Leftrightarrow 0x = 0\) điều này đúng với mọi $x \in R$.
Vậy với \(m = 2\) thì phương trình có vô số nghiệm.
Phép tính \(\dfrac{{24x{y^2}{z^2}}}{{12{x^2}z}}.\dfrac{{4{x^2}y}}{{6x{y^4}}}\) có kết quả là
-
A.
\(\dfrac{{24z}}{{18y}}\) .
-
B.
\(\dfrac{{24xz}}{{18xy}}\).
-
C.
\(\dfrac{{4x}}{{3y}}\).
-
D.
\(\dfrac{{4z}}{{3y}}\).
Đáp án : D
Bước 1: Thực hiện phép nhân phân thức: Muốn nhân hai phân thức , ta nhân tử thức với nhau, mẫu thức với nhau.
Bước 2: Rút gọn phân thức thu được.
Ta có \(\dfrac{{24x{y^2}{z^2}}}{{12{x^2}z}}.\dfrac{{4{x^2}y}}{{6x{y^4}}}\)\( = \dfrac{{24x{y^2}{z^2}.4{x^2}y}}{{12{x^2}z.6x{y^4}}} = \dfrac{{96{x^3}{y^3}{z^2}}}{{72{x^3}{y^4}z}} = \dfrac{{4z}}{{3y}}\) .
Dao động điện từ trong mạch LC tắt càng nhanh khi ?
-
A.
Tụ điện có điện dung càng lớn.
-
B.
Mạch có điện trở càng lớn.
-
C.
Mạch có tần số riêng càng lớn.
-
D.
Cuộn dây có độ tự cảm càng lớn.
Đáp án : B
Ta có năng lượng mất mát khi trong mạch có điện trở R là : \(Q = {I^2}Rt = \dfrac{{I_0^2}}{2}Rt\)
=> Sự tắt dần nhanh hay chậm phụ thuộc vào điện trở R
Cho biết \(3{y^2} - 3y\left( {y - 2} \right) = 36\). Giá trị của $y$ là:
-
A.
5
-
B.
6
-
C.
7
-
D.
8
Đáp án : B
Biến đổi vế trái bằng cách sử dụng quy tắc nhân đơn thức với đa thức rồi cộng trừ các hạng tử đồng dạng
Từ đó tìm \(y.\)
\(\begin{array}{l}3{y^2} - 3y\left( {y - 2} \right) = 36\\ \Leftrightarrow 3{y^2} - 3y.y - 3y\left( { - 2} \right) = 36\\ \Leftrightarrow 3{y^2} - 3{y^2} + 6y = 36\\ \Leftrightarrow 6y = 36 \\\Leftrightarrow y = 6\end{array}\)
Cho hình bình hành $ABCD$ , $O$ là giao điểm của hai đường chéo. Một đường thẳng đi qua $O$ cắt các cạnh $AB$ và $CD$ theo thứ tự ở $M$ và $N$ . Chọn khẳng định đúng .
-
A.
Điểm $M$ đối xứng với điểm $N$ qua$O$ .
-
B.
Điểm $M$ đối xứng với điểm $O$ qua$N$.
-
C.
Điểm $N$ đối xứng với điểm $O$ qua$M$.
-
D.
Điểm $A$ đối xứng với điểm $B$ qua$M$.
Đáp án : A
Từ hai tam giác bằng nhau suy ra \(O\) là trung điểm \(MN\) nên $M$ đối xứng với điểm $N$ qua $O$
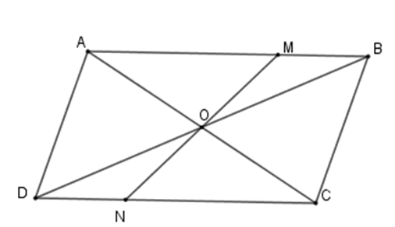
Xét tam giác \(\Delta OMB\) và \(\Delta OND\) có
+ \(\widehat {MOB} = \widehat {NOD}\) (đối đỉnh)
+ \(OB = OD\) (tính chất hình bình hành)
+ \(\widehat {MBO} = \widehat {NDO}\) (so le trong)
Nên \(\Delta OMB = \Delta OND\,\left( {g - c - g} \right) \Rightarrow OM = ON\) (hai cạnh tương ứng)
Suy ra điểm $M$ đối xứng với điểm $N$ qua $O$.
Bất phương trình $2{(x + 2)^2} < 2x(x + 2) + 4$ có nghiệm là
-
A.
$x > - 1$
-
B.
$x > 1$
-
C.
$x \ge - 1$
-
D.
$x < - 1$
Đáp án : D
- Khai triển các hằng đẳng thức - Bỏ dấu ngoặc
- Áp dụng quy tắc chuyển vế và quy tắc nhân với một số để giải bất phương trình.
$\begin{array}{l}\;2{(x + 2)^2} < 2x(x + 2) + 4\\ 2{x^2} + 8x + 8 < 2{x^2} + 4x + 4\\ 4x < - 4\\ x < - 1\end{array}$
Vậy \(x < - 1\) .
Tính thể tích của hình chóp tam giác đều có tất cả các cạnh đều bằng $6\,cm$ (làm tròn đến chữ số thập phân thứ hai).
-
A.
\(24,64\,c{m^3}\)
-
B.
\(25,46\,c{m^3}\)
-
C.
\(26,46\,c{m^3}\)
-
D.
\(26,64\,c{m^3}\)
Đáp án : B
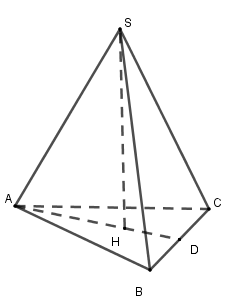
Chóp tam giác đều \(S.ABC\) có \(SH \bot \left( {ABC} \right)\) nên \(H\) là trọng tâm tam giác \(ABC\) và \(D\) là trung điểm \(BC\) .
Áp dụng định lý Pytago cho tam giác \(ABD\) vuông tại $D$ ta có
\(AD = \sqrt {A{B^2} - B{D^2}} \)\( = \sqrt {{6^2} - {3^2}} = 3\sqrt 3 \) nên diện tích đáy \(S = \dfrac{1}{2}AD.BC \)\( = \dfrac{1}{2}.3\sqrt 3 .6 = 9\sqrt 3 \,c{m^2}\) .
Vì \(H\) là trọng tâm tam giác \(ABC \Rightarrow AH = \dfrac{2}{3}AD = \dfrac{2}{3}.3\sqrt 3 = 2\sqrt 3 \) .
Áp dụng định lý Pytago cho tam giác \(ASH\) vuông tại \(H\) ta được \(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{6^2} - {{\left( {2\sqrt 3 } \right)}^2}} = 2\sqrt 6 \)
Từ đó thể tích hình chóp là \(V = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.2\sqrt 6 .9\sqrt 3 \approx 25,46\,c{m^3}\) .
Hình chữ nhật có chiều dài giảm đi $5$ lần và chiều rộng tăng lên \(5\) lần, khi đó diện tích của hình chữ nhật
-
A.
Không thay đổi.
-
B.
Tăng \(5\) lần.
-
C.
Giảm \(5\) lần.
-
D.
Giảm \(3\) lần.
Đáp án : A
Sử dụng công thức tính diện tích hình chữ nhật bằng tích chiều dài nhân chiều rộng.
Gọi \(a;b\) lần lượt là chiều dài và chều rộng của hình chữ nhật ban đầu.
Diện tích hình chữ nhật ban đầu là \(S=a.b\)
Nếu giảm chiều dài đi 5 lần thì chiều dài mới là \(a' = \dfrac{1}{5}a \)
Nếu tăng chiều rộng 5 lần thì chiều rộng mới là \(b' = 5b\)
Lúc này, diện tích của hình chữ nhật mới là \(S' = a'.b' = \dfrac{1}{5}a.5b = ab = S\)
Do đó diện tích hình chữ nhật không thay đổi.
Cho tam giác $ABC$ có $AB = 9\,cm,AC = 16\,cm,BC = 20\,cm$ . Khi đó
-
A.
\(\widehat B = \widehat {\dfrac{A}{3}}\)
-
B.
\(\widehat B = \dfrac{2}{3}\widehat A\)
-
C.
\(\widehat B = \widehat {\dfrac{A}{2}}\)
-
D.
\(\widehat B = \widehat C\)
Đáp án : C
+ Kẻ đường phân giác $AE$ của \(\widehat {BAC}\) sau đó sử dụng tính chất đường phân giác của tam giác để tính \(EC\) .
+ Chứng minh \(\Delta ACB \backsim \Delta ECA\) (c-g-c) suy ra mối quan hệ giữa các góc.
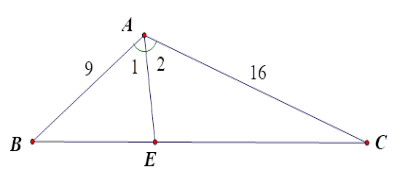
Kẻ đường phân giác $AE$ của \(\widehat {BAC}\) . Theo tính chất đường phân giác, ta có:
$\dfrac{{BE}}{{EC}} = \dfrac{{AB}}{{AC}} = \dfrac{9}{{16}}$ nên
$\dfrac{{BE + EC}}{{EC}} = \dfrac{{9 + 16}}{{16}}$ hay $\dfrac{{20}}{{EC}} = \dfrac{{25}}{{16}}.$
Suy ra $EC = 12,8\,cm$ .
Xét \(\Delta ACB\) và \(\Delta ECA\) có
\(\widehat C\) là góc chung;
$\dfrac{{AC}}{{CB}} = \dfrac{{EC}}{{CA}}$ (vì $\dfrac{{16}}{{20}} = \dfrac{{12,8}}{{16}}$).
Do đó \(\Delta ACB \backsim \Delta ECA\) (c.g.c) suy ra \(\widehat B = {\widehat A_2}\), tức là \(\widehat B = \widehat {\dfrac{A}{2}}\).
Cho hình thang $ABCD{\rm{ }},{\rm{ }}AB$ song song với $CD,$ đường cao $AH.$ Biết \(AB = 7cm;\,CD = 10cm\) , diện tích của $ABCD$ là \(25,5c{m^2}\) thì độ dài $AH$ là:
-
A.
2,5cm
-
B.
3cm
-
C.
3,5cm
-
D.
5cm
Đáp án : B
Từ công thức tính diện tích hình thang bằng nửa tổng hai đáy nhân với đường cao, ta suy ra độ dài đường cao.
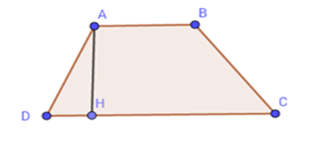
Ta có:
\(\begin{array}{l}{S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2}\\ \Rightarrow AH = \dfrac{{2{S_{ABCD}}}}{{AB + CD}} = \dfrac{{2.25,5}}{{7 + 10}} = 3(cm)\end{array}\)
Tập nghiệm của phương trình \(\dfrac{{ - 7{x^2} + 4}}{{{x^3} + 1}} = \dfrac{5}{{{x^2} - x + 1}} - \dfrac{1}{{x + 1}}\) là
-
A.
\(S = \left\{ {0;1} \right\}\)
-
B.
\(S = \left\{ { - 1} \right\}\)
-
C.
\(S = \left\{ {0; - 1} \right\}\)
-
D.
\(S = \left\{ 0 \right\}\)
Đáp án : D
+ Tìm ĐKXĐ của phương trình
+ Quy đồng mẫu rồi khử mẫu
+ Giải phương trình vừa nhận được
+ Đối chiếu điều kiện rồi kết luận nghiệm
ĐKXĐ: \(x \ne - 1\)
\(\dfrac{{ - 7{x^2} + 4}}{{{x^3} + 1}} = \dfrac{5}{{{x^2} - x + 1}} - \dfrac{1}{{x + 1}}\\\dfrac{{ - 7{x^2} + 4}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = \dfrac{{5\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} - \dfrac{{{x^2} - x + 1}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}}\\\dfrac{{ - 7{x^2} + 4}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = \dfrac{{5\left( {x + 1} \right) - \left( {{x^2} - x + 1} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}}\\ - 7{x^2} + 4 = 5\left( {x + 1} \right) - \left( {{x^2} - x + 1} \right)\\ - 7{x^2} + 4 = 5x + 5 - {x^2} + x - 1\\6{x^2} + 6x = 0\\6x\left( {x + 1} \right) = 0\)
Suy ra \(x = 0\) hoặc \( x + 1 = 0\),
tức là \(x = 0(tm)\) hoặc \(x = - 1(ktm)\)
Vậy phương trình có tập nghiệm là \(S = \left\{ 0 \right\}\)
Phương trình \({x^2} + x = 0\) có số nghiệm là
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
vô nghiệm
-
D.
vô số nghiệm
Đáp án : B
Vế trái đặt nhân tử chung rồi đưa phương trình về dạng phương trình tích $A.B=0$ thì $A = 0$ hoặc $B = 0$
Từ đó tìm $x$.
\({x^2} + x = 0 \\ x\left( {x + 1} \right) = 0 \)
Suy ra \(x = 0\) hoặc \(x + 1 = 0\)
hay \(x = 0\) hoặc \(x = - 1\)
Vậy phương trình có 2 nghiệm $x=-1;x=0$
Giá trị lớn nhất của phân thức $\dfrac{5}{{{x^2} - 6x + 10}}$ là :
-
A.
$5$
-
B.
$ - 5$
-
C.
$2$
-
D.
$ - 2$
Đáp án : A
- Biến đổi mẫu thức đã cho về dạng ${(A + B)^2} + C$
- Đánh giá biểu thức, từ đó tìm GTLN của biểu thức.
Ta có: $\dfrac{5}{{{x^2} - 6x + 10}} = \dfrac{5}{{{x^2} - 6x + 9 + 1}} = \dfrac{5}{{{{(x - 3)}^2} + 1}}$
Vì ${(x - 3)^2} \ge 0 \Rightarrow {(x - 3)^2} + 1 \ge 1 \Rightarrow \dfrac{1}{{{{(x - 3)}^2} + 1}} \le 1 \Rightarrow \dfrac{5}{{{{(x - 3)}^2} + 1}} \le 5$
Vậy GTLN của phân thức là $5$.
Dấu “=” xảy ra khi \({\left( {x - 3} \right)^2} = 0\) hay \(x = 3\).
Tìm \(y\) trong hình vẽ dưới đây.

-
A.
\(17,85\)
-
B.
\(10,75\)
-
C.
\(18,75\)
-
D.
\(15,87\)
Đáp án : C
- Tính \(ID\) theo Pytago
- Áp dụng các phương pháp chứng minh tam giác đồng dạng để tìm ra cặp tam giác đồng dạng phù hợp.
- Suy ra tỉ lệ thức phù hợp, biến đổi tỉ lệ thức để tính giá trị của $x.$
Áp dụng định lý Pitago trong tam giác vuông IAD ta có:
\(\begin{array}{l}\;\;\;\;A{I^2} + A{D^2} = I{D^2}\;\;\\ \Leftrightarrow {4^2} + {3^2} = I{D^2}\\ \Leftrightarrow I{D^2} = 25\\ \Rightarrow ID = 5\end{array}\)
Xét 2 tam giác vuông IAD và CBI có: \(\widehat {IDA} = \widehat {CIB}\;(gt)\)
\( \Rightarrow \Delta IAD \backsim \Delta CBI\;(g - g)\)
\( \Rightarrow \dfrac{{IA}}{{CB}} = \dfrac{{ID}}{{CI}}\)\( \Leftrightarrow \dfrac{4}{{15}} = \dfrac{5}{y} \Leftrightarrow y = \dfrac{{15.5}}{4} = 18,75\)
Vậy \(y = 18,75\).
Cho biết \(\dfrac{{AB}}{{CD}} = \dfrac{5}{7}\) và đoạn thẳng $AB$ ngắn hơn đoạn thẳng $CD$ là $10{\rm{ }}cm.$ Tính độ dài các đoạn thẳng$AB,{\rm{ }}CD$ ?
-
A.
$AB = 35{\rm{ }}cm,{\rm{ }}CD = 25{\rm{ }}cm$
-
B.
$AB = 20{\rm{ }}cm,{\rm{ }}CD = 30{\rm{ }}cm$
-
C.
$AB = 25{\rm{ }}cm,{\rm{ }}CD = 35{\rm{ }}cm$
-
D.
$AB = 30{\rm{ }}cm,{\rm{ }}CD = 20{\rm{ }}cm$
Đáp án : C
- Từ tỉ số đoạn thẳng ta biểu diễn AB theo CD
- Thay vào điều kiện đề bài cho để tính CD, từ đó ta tính được AB
Theo bài ra, ta có: \(\dfrac{{AB}}{{CD}} = \dfrac{5}{7}\)
\( \Rightarrow AB = \dfrac{5}{7}CD\)
Mà đoạn thẳng $AB$ ngắn hơn đoạn thẳng $CD$ là $10{\rm{ }}cm,$ suy ra: \(CD - AB = 10.\)
\(\begin{array}{l} \Rightarrow CD - \dfrac{5}{7}CD = 10 \Leftrightarrow \dfrac{2}{7}CD = 10 \Leftrightarrow CD = \dfrac{{10.7}}{2} = 35\;cm\\ \Rightarrow AB = \dfrac{5}{7}CD = \dfrac{5}{7}.35 = 25\;cm\end{array}\)
Số nguyên nhỏ nhất thỏa mãn bất phương trình $x(5x + 1) + 4(x + 3) > 5{x^2}$ là
-
A.
$x = - 3$
-
B.
$x = 0$
-
C.
\(x = - 1\)
-
D.
\(x = - 2\).
Đáp án : D
Nhân đơn thức với đa thức
Áp dụng quy tắc chuyển vế, nhân với một số âm hoặc dương.
\(\begin{array}{l}\;x(5x + 1) + 4(x + 3) > 5{x^2}\\ \Leftrightarrow 5{x^2} + x + 4x + 12 > 5{x^2}\\ \Leftrightarrow 5x > - 12\\ \Leftrightarrow x > \dfrac{{ - 12}}{5}\end{array}\)
Vậy nghiệm của bất phương trình là \(x > - \dfrac{{12}}{5}.\)
Số nguyên lớn nhất thỏa mãn bất phương trình là \(x = - 2.\)
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
-
A.
\( - 16\)
-
B.
\( - 8\)
-
C.
\(16\)
-
D.
\(8\).
Đáp án : D
Vận dụng tính chất không âm của giá trị tuyệt đối dẫn đến phương pháp bất đẳng thức.
* Nhận xét: Tổng của các số không âm là một số không âm và tổng đó bằng 0 khi và chỉ khi các số hạng của tổng đồng thời bằng 0.
* Cách giải chung: \(\left| A \right| + \left| B \right| = 0\)
Bước1: Đánh giá: \(\left. \begin{array}{l}\left| A \right| \ge 0\\\left| B \right| \ge 0\end{array} \right\} \Rightarrow \left| A \right| + \left| B \right| \ge 0\)
Bước 2: Khẳng định: \(\left| A \right| + \left| B \right| = 0\)\( \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
\({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}\left| {x - 3y} \right| \ge 0\\\left| {y + 4} \right| \ge 0\end{array} \right\} \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} \ge 0\\ \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0 \Leftrightarrow \left\{ \begin{array}{l}x - 3y = 0\\y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3.( - 4) = 0\\y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 12\\y = - 4\end{array} \right.\end{array}\)
Vậy nghiệm của phương trình là $x = - 12$ và $y = - 4.$
Suy ra \(y - x = - 4 - \left( { - 12} \right) = 8.\)
Cho tam giác ABC, M thuộc cạnh AB, N thuộc cạnh BC, biết \(\frac{{MA}}{{MB}} = \frac{{NC}}{{NB}} = \frac{2}{5},MN = 15\left( {cm} \right)\). Tính độ dài cạnh AC.
-
A.
AC = 21 (cm).
-
B.
AC = 37,5 (cm)
-
C.
AC = 52,5 (cm).
-
D.
AC = 25 (cm).
Đáp án : A
Dựa vào định lí Thales và định lý Thales đảo.
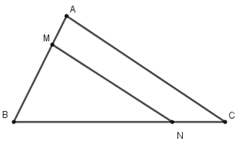
Ta có: \(\frac{{MA}}{{MB}} = \frac{{NC}}{{NB}} = \frac{2}{5} \Rightarrow MN\parallel AC\)
\(\frac{{MA}}{{MB}} = \frac{2}{5},MA + MB = AB\)
\( \Rightarrow \frac{{MA}}{{AB}} = \frac{2}{7};\frac{{MB}}{{AB}} = \frac{5}{7}\)
Áp dụng định lý Talet trong tam giác ABC với MN//AC ta có:
\(\frac{{MB}}{{AB}} = \frac{{MN}}{{AC}} = \frac{5}{7}\)
\( \Rightarrow AC = \frac{{7MN}}{5} = \frac{{7.15}}{5} = 21\left( {cm} \right)\)
Cho đa thức \(F\left( x \right) = a{x^2} + bx + c\) với các hệ số \(a,\,b,\,c\) thỏa mãn \(11a - b + 5c = 0\).
Chọn câu đúng.
-
A.
\(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) cùng dấu dương
-
B.
\(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) cùng dấu âm
-
C.
\(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) có thể cùng dấu hoặc trái dấu
-
D.
\(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) luôn trái dấu
Đáp án : D
Tính \(F\left( 1 \right)\) và \(F\left( { - 2} \right)\), chứng tỏ \(3F\left( 1 \right)\) và \(2F\left( { - 2} \right)\) trái dấu, từ đó suy ra mối quan hệ về dấu của \(F\left( 1 \right)\) và \(F\left( { - 2} \right)\).
Ta có:
\(\begin{array}{l}F\left( 1 \right) = a + b + c \Rightarrow 3F\left( 1 \right) = 3a + 3b + 3c\\F\left( { - 2} \right) = 4a - 2b + c \Rightarrow 2F\left( { - 2} \right) = 8a - 4b + 2c\end{array}\).
Xét:
\(\begin{array}{l}3F\left( 1 \right) = 3a + 3b + 3c = 11a - 8a + 4b - b + 5c - 2c\\ = \left( {11a - b + 5c} \right) - \left( {8a - 4b + 2c} \right) = 0 - 2F\left( { - 2} \right) = - 2F\left( { - 2} \right)\\ \Rightarrow 3F\left( 1 \right) = - 2F\left( { - 2} \right)\end{array}\).
Suy ra: \(F\left( 1 \right)\) và \(F\left( { - 2} \right)\) không thể cùng dấu hay \(F\left( 1 \right);F\left( { - 2} \right)\) trái dấu.
Có bao nhiêu nghiệm của đa thức \(2{x^2} + 7x - 9\)?
-
A.
\(3\)
-
B.
\(0\)
-
C.
\(1\)
-
D.
\(2\)
Đáp án : D
Cho đa thức đó bằng \(0\) và giải tìm nghiệm.
Ta có:
\(\begin{array}{l}\,\,\,2{x^2} + 7x - 9 = 0\\ \Leftrightarrow 2{x^2} + 9x - 2x - 9 = 0\\ \Leftrightarrow x\left( {2x + 9} \right) - \left( {2x + 9} \right) = 0\\ \Leftrightarrow \left( {2x + 9} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x + 9 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{ - 9}}{2}\\x = 1\end{array} \right.\end{array}\).
Vậy có hai nghiệm là \(x = - \dfrac{9}{2};x = 1.\)
Cho \(\Delta ABC\) có \(AB = AC\), \(\widehat A = 2\widehat B\) có dạng đặc biệt nào:
-
A.
Tam giác vuông
-
B.
Tam giác đều
-
C.
Tam giác cân
-
D.
Tam giác vuông cân
Đáp án : D
Áp dụng định lý tổng ba góc trong tam giác, tính chất tam giác cân, dấu hiệu nhận biết tam giác vuông cân.
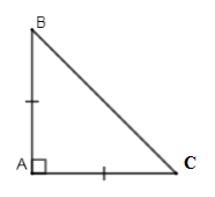
Vì \(AB = AC\,\left( {gt} \right) \Rightarrow \Delta ABC\) cân tại \(A\) (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \angle B = \angle C\) (tính chất tam giác cân).
Ta có: \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc của tam giác).
Mà \(\left\{ \begin{array}{l}\angle B = \angle C\\\angle A = 2\angle B\\\angle A + \angle B + \angle C = {180^0}\end{array} \right. \\\Rightarrow 2\angle B + 2\angle C = {180^0} \\\Rightarrow \angle B + \angle C = {180^0}:2 = {90^0}\\ \Rightarrow \angle A = {180^0} - {90^0} = {90^0}\)
\( \Rightarrow \Delta ABC\) là tam giác vuông cân tại \(A\) (dấu hiệu nhận biết tam giác vuông cân).
Cho \(B = \dfrac{{x - 1}}{{x - 2}}\). Số giá trị của \(x \in Z\) để \(B \in \mathbb{Z}\) là:
-
A.
3
-
B.
0
-
C.
2
-
D.
-2
Đáp án : C
Sử dụng kiến thức biến đổi biểu thức hữu tỉ; tìm điều kiện để biểu thức có giá trị nguyên.
+) Tìm ĐKXĐ của B.
+) Tách B về dạng \(B = a + \dfrac{b}{{MS}},\,\,a,\,\,b \in Z.\)
+) Đề \(B \in Z\) thì \(\dfrac{b}{{MS}} \in Z \Leftrightarrow MS \in Ư\left( b \right).\)
+) Tìm Ư(b) sau đó lập bảng, giải phương trình tìm x.
+) Xét xem các giá trị của x có thỏa mãn ĐKXĐ của bài toán hay không rồi kết luận x.
ĐKXĐ: \(x \ne 2.\)
Ta có: \(B = \dfrac{{x - 1}}{{x - 2}} = 1 + \dfrac{1}{{x - 2}}\)
\(B = 1 + \dfrac{1}{{x - 2}} \in Z \Leftrightarrow \dfrac{1}{{x - 2}} \in Z \Leftrightarrow x - 2 \in Ư(1) = \left\{ { \pm 1} \right\}\).
