Đề thi khảo sát chất lượng đầu năm Toán 9 - Đề số 6
Đề bài
Cho: \({a^3} + {b^3} + {c^3} = 3abc\) thì
-
A.
\(a = b = c\) hoặc \(a + b + c = 0\).
-
B.
\(a = b = c\)
-
C.
\(a = b = c = 0\)
-
D.
\(a = b = c\) hoặc \(a + b + c = 1\)
Hình hộp chữ nhật \(ABC{\rm{D}}.A'B'C'D'\) có đáy $ABCD$ là hình vuông cạnh $a$ và diện tích hình chữ nhật \(A{\rm{D}}C'B'\) bằng \(2{{\rm{a}}^2}\), diện tích xung quanh của hình hộp chữ nhật bằng bao nhiêu?
-
A.
\( S_{xq}= 4{{\rm{a}}^2}\sqrt 3 \)
-
B.
\(S_{xq} = 2{{\rm{a}}^2}\sqrt 3 \)
-
C.
\( S_{xq}= 4{{\rm{a}}^2} \)
-
D.
\( S_{xq}= 4{{\rm{a}}^2}\sqrt 2 \)
Cho hình lăng trụ đứng \(ABC{\rm{D}}.A'B'C'D'\) có đáy là hình thang vuông ABCD vuông tại A, B \(\left( {A{\rm{D//}}BC} \right)\) và BC = 12 cm, AD = 16 cm, CD = 5 cm, đường cao ${\rm{AA}}' = 6\;cm$. Thể tích của hình lăng trụ là:
-
A.
$200\;c{m^3}$
-
B.
$250\;c{m^3}$
-
C.
$252\;c{m^3}$
-
D.
$410\;c{m^3}$
Hình lăng trụ đứng tam giác có
-
A.
\(5\) mặt, \(6\) đỉnh và \(9\) cạnh
-
B.
\(4\) mặt, \(6\) đỉnh và \(6\) cạnh
-
C.
\(5\) mặt, \(9\) đỉnh và \(6\) cạnh
-
D.
\(3\) mặt, \(6\) đỉnh và \(6\) cạnh
Cho tam giác $MNP$ vuông ở $M$ và có đường cao $MK$ .
-
A.
$\Delta KNM$ \( \backsim \)$\Delta MNP$ \( \backsim \) $\Delta KMP.$
-
B.
$M{K^2} = NK.PK$
-
C.
Cả A, B đều sai
-
D.
Cả A, B đều đúng
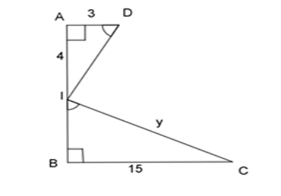
Tìm \(y\) trong hình vẽ dưới đây.
-
A.
\(17,85\)
-
B.
\(10,75\)
-
C.
\(18,75\)
-
D.
\(15,87\)
Một người đo chiều cao của cây nhờ 1 cọc chôn xuống đất, cọc cao 2,45 m và đặt xa cây 1,36 m. Sau khi người ấy lùi ra xa cách cọc 0,64 m thì người ấy nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu? Biết khoảng cách từ chân đến mắt người ấy là 1,65 m.
-
A.
\(4,51\;m\)
-
B.
\(5,14\;m\)
-
C.
\(5,41\;m\)
-
D.
\(4,15\;m\)
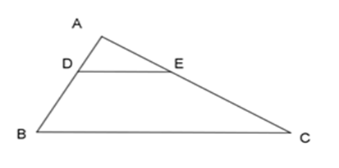
Cho hình vẽ biết \(DE//BC\). Khẳng định nào sau đây là đúng?
-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\)
-
B.
\(AD.AE = AB.AC\)
-
C.
\(\dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC}}\)
-
D.
\(DE.AD = AB.BC\)
Cho \(\Delta ABC\), đường phân giác góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,{\rm{ }}AD = 6{\rm{ }}cm.$ Tính $AC = $ ?
-
A.
$6{\rm{ }}cm$
-
B.
$9{\rm{ }}cm$
-
C.
$12{\rm{ }}cm$
-
D.
$15{\rm{ }}cm$
Cho hình chữ nhật ABCD có \(AD = 8cm,\;AB = 9cm\). Các điểm $M,{\rm{ }}N$ trên đường chéo $BD$ sao cho $BM = MN = ND.$ Tính diện tích tam giác $CMN.$
-
A.
\(12c{m^2}\)
-
B.
\(24c{m^2}\)
-
C.
\(36c{m^2}\)
-
D.
\(6c{m^2}\)
Hình chữ nhật có chiều dài tăng 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật
-
A.
không thay đổi
-
B.
tăng \(4\) lần
-
C.
giảm \(2\) lần
-
D.
tăng \(2\) lần
Một đa giác lồi \(10\) cạnh thì có số đường chéo là:
-
A.
\(35\)
-
B.
\(30\)
-
C.
\(70\)
-
D.
\(27\)
Cho \(\Delta ABC\) vuông tại $A,$ đường cao $AH.$ Gọi $I$ và $K$ lần lượt là hình chiếu của $H$ lên $AB$ và $AC.$ Tam giác \(AIK\) đồng dạng với tam giác nào dưới đây?
-
A.
$ACB$
-
B.
$ABC$
-
C.
$CAB$
-
D.
\(BAC\)
Phương trình \(\left| {2x - 5} \right| = 1\) có nghiệm là:
-
A.
\(x = 3;x = 2\)
-
B.
\(x = \dfrac{5}{2};x = 2\)
-
C.
\(x = 1;x = 2\)
-
D.
$x = 0,5{\rm{ }};x = 1,5$
Cho hình thang $ABCD\left( {AB//CD} \right),{\rm{ }}M$ là trung điểm của $AD,{\rm{ }}N$ là trung điểm của $BC.$ Gọi $I,{\rm{ }}K$ theo thứ tự là giao điểm của $MN$ với $BD,{\rm{ }}AC.$ Cho biết $AB = 6cm,{\rm{ }}CD = 14cm.$ Tính độ dài $MI,{\rm{ }}IK.$
-
A.
\(MI = 4cm;IK = 7cm.\)
-
B.
\(MI = 4cm;IK = 3cm.\)
-
C.
\(MI = 3cm;IK = 7cm.\)
-
D.
\(MI = 3cm;IK = 4cm.\)
Cho tứ giác $ABCD,$ có \(\widehat A = {70^0},\) \(\widehat B = {120^0},\) \(\widehat D = {50^0},\) Số đo \(\widehat C\) là:
-
A.
\({100^0}\)
-
B.
\({105^0}\)
-
C.
\({120^0}\)
-
D.
\({115^0}\)
Trong các tứ giác sau, tứ giác nào là hình có \(4\) trục đối xứng?
-
A.
Hình chữ nhật
-
B.
Hình vuông
-
C.
Hình bình hành
-
D.
Hình thoi
Nghiệm của bất phương trình \(\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\) là
-
A.
$x < - 1$
-
B.
$x < 1$
-
C.
\(x > 1\)
-
D.
\(x > - 1\).
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
-
A.
\( - 16\)
-
B.
\( - 8\)
-
C.
\(16\)
-
D.
\(8\).
Cho tam giác $ABC.$ Gọi $D,E,F\;$ theo thứ tự là trung điểm của $AB,BC,CA.$ Gọi $M,N,P,Q$ theo thứ tự là trung điểm của $AD,AF,EF,ED.\;$
$\Delta ABC$ có điều kiện gì thì $MNPQ$ là hình chữ nhật?
-
A.
$\Delta ABC$ cân tại $A$
-
B.
$\Delta ABC$ cân tại $B$
-
C.
$\Delta ABC$ cân tại $C$
-
D.
$\Delta ABC$ vuông tại $A$
Tính giá trị biểu thức \(P = \left( { - 4{x^3}{y^3} + {x^3}{y^4}} \right):2x{y^2} - xy\left( {2x - xy} \right)\) cho \(x = 1,y = \dfrac{{ - 1}}{2}\);
-
A.
\(P = - \dfrac{{19}}{8}\)
-
B.
\(P = \dfrac{{19}}{8}\)
-
C.
\(P = \dfrac{8}{{19}}\)
-
D.
\(P = \dfrac{9}{8}\)
Thực hiện phép tính \(A = \left( {6{x^3} - 5{x^2} + 4x - 1} \right):\left( {2{x^2} - x + 1} \right)\) ta được
-
A.
\(3x - 1\)
-
B.
\(3x + 1\)
-
C.
\(3x\)
-
D.
\(3\)
Phân tích đa thức sau thành nhân tử: \({x^3} - 5x + 4\) ta được
-
A.
\(\left( {x + 1} \right)\left( {{x^2} + x - 4} \right)\)
-
B.
\(\left( {x - 1} \right)\left( {{x^2} - x - 4} \right)\)
-
C.
\(\left( {x - 1} \right)\left( {{x^2} + x - 4} \right)\)
-
D.
\(\left( {x - 1} \right)\left( {{x^2} + x + 4} \right)\)
Rút gọn đa thức \(16{x^2} - 4x + \dfrac{1}{4}\) ta được kết quả nào sau đây?
-
A.
\({\left( {4x - \dfrac{1}{2}} \right)^2}\)
-
B.
\({\left( {x - \dfrac{1}{2}} \right)^2}\)
-
C.
\({\left( {4x + \dfrac{1}{2}} \right)^2}\)
-
D.
\({\left( {x + \dfrac{1}{2}} \right)^2}\)
Tìm \(x\) biết \(\left( {x + 2} \right)(x + 3) - \left( {x - 2} \right)\left( {x + 5} \right) = 6\)
-
A.
\(x = - 5.\)
-
B.
\(x = 5.\)
-
C.
\(x = - 10.\)
-
D.
\(x = - 1.\)
Cho $Q = \left( {\dfrac{{{x^2} + 3x}}{{{x^3} + 3{x^2} + 9x + 27}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^3} - 3{x^2} + 9x - 27}}} \right).$ Rút gọn $Q$ ta được.
-
A.
\(Q = \dfrac{1}{{{x^2} + 9}}\)
-
B.
\(Q = \dfrac{{x - 3}}{{x + 3}}\)
-
C.
\(Q = \dfrac{1}{{x - 3}}\)
-
D.
\(Q = \dfrac{{x + 3}}{{x - 3}}\)
Rút gọn biểu thức \(\dfrac{{{x^4} + 4{x^2} + 5}}{{5{x^3} + 5}}\,\, \cdot \,\,\dfrac{{2x}}{{{x^2} + 4}}\,\, \cdot \,\,\dfrac{{3{x^3} + 3}}{{{x^4} + 4{x^2} + 5}}\) ta được:
-
A.
\(\dfrac{{2x}}{{5({x^2} + 4)}}\)
-
B.
\(\dfrac{{6x}}{{5({x^2} + 4)}}\)
-
C.
\(\dfrac{{3x}}{{5({x^2} + 4)}}\)
-
D.
\(\dfrac{x}{{5({x^2} + 4)}}\)
Thực hiện phép tính sau: $\dfrac{{{x^3}}}{{{x^2} + 1}} + \dfrac{x}{{{x^2} + 1}}$
-
A.
$ - x$
-
B.
$2x$
-
C.
$\dfrac{x}{2}$
-
D.
$x$
Kết quả của phép tính $\dfrac{1}{x} + \dfrac{1}{{x(x + 1)}} + ... + \dfrac{1}{{(x + 9)(x + 10)}}$ là:
-
A.
$\dfrac{{x + 20}}{{x(x + 10)}}$
-
B.
$\dfrac{{x + 9}}{{x + 10}}$
-
C.
$\dfrac{1}{{x + 10}}$
-
D.
$\dfrac{1}{{x(x + 1)...(x + 10)}}$
Tổng các nghiệm của phương trình: \(\dfrac{1}{{{x^2} + 4x + 3}} + \dfrac{1}{{{x^2} + 8x + 15}} + \dfrac{1}{{{x^2} + 12x + 35}} + \dfrac{1}{{{x^2} + 16x + 63}} = \dfrac{1}{5}\) là
-
A.
\(10\)
-
B.
\( - 10\)
-
C.
\( - 11\)
-
D.
\(12\)
Giải phương trình: \(2x\left( {x - 5} \right) + 21 = x\left( {2x + 1} \right) - 12\) ta được nghiệm \({x_0}.\) Chọn câu đúng.
-
A.
\({x_0} = 4\)
-
B.
\({x_0} < 4\)
-
C.
\({x_0} > 4\)
-
D.
\({x_0} > 5\)
Phương trình \(\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} = 1\) có nghiệm là
-
A.
\(x = - \dfrac{1}{2}\)
-
B.
\(x = \dfrac{5}{2}\)
-
C.
\(x = \dfrac{1}{2}\)
-
D.
\(x = - \dfrac{5}{2}\)
Hình vẽ dưới đây là biểu diễn tập nghiệm của bất phương trình nào?
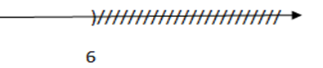
-
A.
$x - 1 \ge 5$
-
B.
$x + 1 \le 7$
-
C.
$x + 3 < 9$
-
D.
$x + 1 > 7$.
Lời giải và đáp án
Cho: \({a^3} + {b^3} + {c^3} = 3abc\) thì
-
A.
\(a = b = c\) hoặc \(a + b + c = 0\).
-
B.
\(a = b = c\)
-
C.
\(a = b = c = 0\)
-
D.
\(a = b = c\) hoặc \(a + b + c = 1\)
Đáp án : A
Sử dụng hằng đẳng thức: \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\) để biến đổi giả thiết.
Từ đẳng thức đã cho suy ra \({a^3} + {b^3} + {c^3} - 3abc = 0\)
${b^3} + {c^3} = \left( {b + c} \right)\left( {{b^2} + {c^2} - bc} \right) $$= \left( {b + c} \right)\left[ {{{\left( {b + c} \right)}^2} - 3bc} \right] $$= {\left( {b + c} \right)^3} - 3bc\left( {b + c} \right)$
$ \Rightarrow {a^3} + {b^3} + {c^3} - 3abc $$= {a^3} + \left( {{b^3} + {c^3}} \right) - 3abc $
$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc= {a^3} + {\left( {b + c} \right)^3} - 3bc\left( {b + c} \right) - 3abc$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc $$= \left( {a + b + c} \right)\left( {{a^2} - a\left( {b + c} \right) + {{\left( {b + c} \right)}^2}} \right) - \left[ {3bc\left( {b + c} \right) + 3abc} \right]$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} - a\left( {b + c} \right) + {{\left( {b + c} \right)}^2}} \right) - 3bc\left( {a + b + c} \right)$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} - a\left( {b + c} \right) + {{\left( {b + c} \right)}^2} - 3bc} \right)$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} - ab - ac + {b^2} + 2bc + {c^2} - 3bc} \right)$$ \Leftrightarrow {a^3} + {b^3} + {c^3} - 3abc = \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2} - ab - ac - bc} \right)$
Do đó nếu \({a^3} + {b^3} + {c^3} - 3abc = 0\) thì \(a + b + c = 0\) hoặc \({a^2} + {b^2} + {c^2} - ab - bc - ac = 0\)
Mà \({a^2} + {b^2} + {c^2} - ab - bc - ac = \dfrac{1}{2}.\left[ {{{\left( {a - b} \right)}^2} + {{\left( {a - c} \right)}^2} + {{\left( {b - c} \right)}^2}} \right]\) suy ra \(a = b = c\).
Hình hộp chữ nhật \(ABC{\rm{D}}.A'B'C'D'\) có đáy $ABCD$ là hình vuông cạnh $a$ và diện tích hình chữ nhật \(A{\rm{D}}C'B'\) bằng \(2{{\rm{a}}^2}\), diện tích xung quanh của hình hộp chữ nhật bằng bao nhiêu?
-
A.
\( S_{xq}= 4{{\rm{a}}^2}\sqrt 3 \)
-
B.
\(S_{xq} = 2{{\rm{a}}^2}\sqrt 3 \)
-
C.
\( S_{xq}= 4{{\rm{a}}^2} \)
-
D.
\( S_{xq}= 4{{\rm{a}}^2}\sqrt 2 \)
Đáp án : A
- Áp dụng công thức tính diện tích xung quanh hình hộp chữ nhật \({S_{xq}} = 2ph\) (với p là nửa chu vi đáy) và công thức tính diện tích hình chữ nhật, định lý Pytago
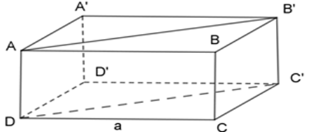
Ta có \(A{\rm{D}}C'B'\) là hình chữ nhật.
\( \Rightarrow {S_{A{\rm{D}}C'B'}} = A{\rm{D}}.DC' = 2{{\rm{a}}^2} \Rightarrow a.DC' = 2{{\rm{a}}^2} \Rightarrow DC' = 2{\rm{a}}\)
Xét tam giác vuông \(CC'D\) ta có:
\(CC{'^2} + C{{\rm{D}}^2} = C'{D^2} \Leftrightarrow CC{'^2} + {a^2} = {(2{\rm{a}})^2} \Leftrightarrow CC{'^2} = 4{{\rm{a}}^2} - {a^2} = 3{{\rm{a}}^2} \Rightarrow CC' = a\sqrt 3 \)
Vậy diện tích xung quanh của hình hộp chữ nhật là:
Sxq \( = 2.p.CC' = 2.\dfrac{{4{\rm{a}}}}{2}.a\sqrt 3 = 4{{\rm{a}}^2}\sqrt 3 \)
Cho hình lăng trụ đứng \(ABC{\rm{D}}.A'B'C'D'\) có đáy là hình thang vuông ABCD vuông tại A, B \(\left( {A{\rm{D//}}BC} \right)\) và BC = 12 cm, AD = 16 cm, CD = 5 cm, đường cao ${\rm{AA}}' = 6\;cm$. Thể tích của hình lăng trụ là:
-
A.
$200\;c{m^3}$
-
B.
$250\;c{m^3}$
-
C.
$252\;c{m^3}$
-
D.
$410\;c{m^3}$
Đáp án : C
- Kẻ $CH \bot AD$ tại H, áp dụng định lý Pytago
- Áp dụng công thức tính thể tích hình lăng trụ đứng: $V = {S_đ}.h.$
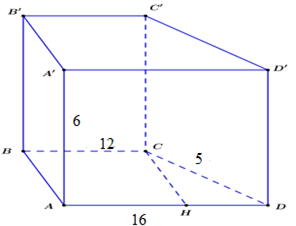
Trong mp $\left( {ABCD} \right)$ kẻ $CH$ vuông góc với $AD$ tại $H.$
Khi đó ta có $ABCH$ là hình chữ nhật. \(\left( {do\;\;\widehat A = \widehat B = \widehat H = 90^\circ } \right)\)
\( \Rightarrow BC = AH = 12\;cm \)\(\Rightarrow H{\rm{D}} = A{\rm{D}} - AH = 16 - 12 = 4\;cm\)
Xét tam giác $HCD$ vuông tại $H$ ta có:
\(H{C^2} + H{{\rm{D}}^2} = C{{\rm{D}}^2} \Leftrightarrow H{C^2} = C{{\rm{D}}^2} - H{{\rm{D}}^2} = {5^2} - {4^2} = 25 - 16 = 9 \Rightarrow HC = 3\;cm\)
Vậy thể tích của hình lăng trụ là:
$V{\rm{ }} = {\rm{ }}{S_{ABCD}}.h{\rm{ }} = {\rm{ }}{S_{ABCD}}.AA'$ \( = \dfrac{1}{2}AA'.\left( {BC + AD} \right).CH = \dfrac{1}{2}.3.(12 + 16).6 = 252\;c{m^3}\) \(\)
Hình lăng trụ đứng tam giác có
-
A.
\(5\) mặt, \(6\) đỉnh và \(9\) cạnh
-
B.
\(4\) mặt, \(6\) đỉnh và \(6\) cạnh
-
C.
\(5\) mặt, \(9\) đỉnh và \(6\) cạnh
-
D.
\(3\) mặt, \(6\) đỉnh và \(6\) cạnh
Đáp án : A
Sử dụng kiến thức về hình lăng trụ đứng tam giác hoặc vẽ hình rồi đếm số mặt, số đỉnh, số cạnh.
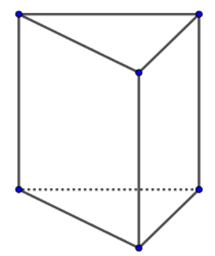
Quan sát hình vẽ ta thấy hình lăng trụ đứng tam giác có \(5\) mặt, \(6\) đỉnh và \(9\) cạnh.
Cho tam giác $MNP$ vuông ở $M$ và có đường cao $MK$ .
-
A.
$\Delta KNM$ \( \backsim \)$\Delta MNP$ \( \backsim \) $\Delta KMP.$
-
B.
$M{K^2} = NK.PK$
-
C.
Cả A, B đều sai
-
D.
Cả A, B đều đúng
Đáp án : D
- Áp dụng phương pháp chứng minh tam giác đồng dạng và biến đổi tỉ lệ thức để thực hiện yêu cầu của bài toán.
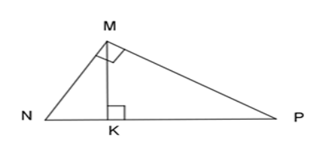
+) Xét 2 tam giác vuông $\Delta KNM$ và $\Delta MNP$ có: \(\widehat N\) chung
nên $\Delta KNM$\( \backsim \) $\Delta MNP$ (g.g) (1)
Xét 2 tam giác vuông $\Delta KMP$ và $\Delta MNP$ có: \(\widehat P\) chung
nên $\Delta KMP$\( \backsim \) $\Delta MNP$ (g.g) (2)
Từ (1) và (2) suy ra: $\Delta KNM$ \( \backsim \) $\Delta KMP$ (theo t/c bắc cầu).
Vậy $\Delta KNM$\( \backsim \) $\Delta MNP$\( \backsim \)$\Delta KMP$ nên A đúng.
+) Theo chứng minh trên: $\Delta KNM$ \( \backsim \) $\Delta KMP.$
\( \Rightarrow \dfrac{{MK}}{{PK}} = \dfrac{{NK}}{{MK}}\)
\( \Leftrightarrow M{K^2} = NK.PK\) nên B đúng.
Vậy cả A, B đều đúng.
Tìm \(y\) trong hình vẽ dưới đây.

-
A.
\(17,85\)
-
B.
\(10,75\)
-
C.
\(18,75\)
-
D.
\(15,87\)
Đáp án : C
- Tính \(ID\) theo Pytago
- Áp dụng các phương pháp chứng minh tam giác đồng dạng để tìm ra cặp tam giác đồng dạng phù hợp.
- Suy ra tỉ lệ thức phù hợp, biến đổi tỉ lệ thức để tính giá trị của $x.$
Áp dụng định lý Pitago trong tam giác vuông IAD ta có:
\(\begin{array}{l}\;\;\;\;A{I^2} + A{D^2} = I{D^2}\;\;\\ \Leftrightarrow {4^2} + {3^2} = I{D^2}\\ \Leftrightarrow I{D^2} = 25\\ \Rightarrow ID = 5\end{array}\)
Xét 2 tam giác vuông IAD và CBI có: \(\widehat {IDA} = \widehat {CIB}\;(gt)\)
\( \Rightarrow \Delta IAD \backsim \Delta CBI\;(g - g)\)
\( \Rightarrow \dfrac{{IA}}{{CB}} = \dfrac{{ID}}{{CI}}\)\( \Leftrightarrow \dfrac{4}{{15}} = \dfrac{5}{y} \Leftrightarrow y = \dfrac{{15.5}}{4} = 18,75\)
Vậy \(y = 18,75\).
Một người đo chiều cao của cây nhờ 1 cọc chôn xuống đất, cọc cao 2,45 m và đặt xa cây 1,36 m. Sau khi người ấy lùi ra xa cách cọc 0,64 m thì người ấy nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu? Biết khoảng cách từ chân đến mắt người ấy là 1,65 m.
-
A.
\(4,51\;m\)
-
B.
\(5,14\;m\)
-
C.
\(5,41\;m\)
-
D.
\(4,15\;m\)
Đáp án : D
- Tìm ra các cặp tam giác đồng dạng phù hợp.
- Áp dụng tính chất của tam giác đồng dạng để tìm ra yêu cầu của đề bài.
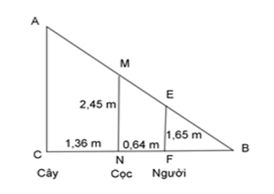
Ta mô tả vị trí cây, cọc và người như hình vẽ bên.
Xét \(\Delta BFE\) và \(\Delta BNM\) ta có:
\(\widehat B\;chung\)
\(\widehat {BEF} = \widehat {BMN}\) (vì \(EF//MN\), cặp góc đồng vị bằng nhau)
\( \Rightarrow \Delta BFE \backsim \Delta BNM\;(g - g)\)
\(\begin{array}{l} \Rightarrow \dfrac{{BF}}{{BN}} = \dfrac{{FE}}{{NM}} \Leftrightarrow \dfrac{{BF}}{{BF + FN}} = \dfrac{{FE}}{{NM}} \Leftrightarrow \dfrac{{BF}}{{BF + 0,64}} = \dfrac{{1,65}}{{2,45}}\\ \Leftrightarrow 1,65\left( {BF + 0,64} \right) = 2,45.BF\\ \Leftrightarrow BF = 1,32\;\;m.\end{array}\)
Xét \(\Delta BFE\) và \(\Delta BCA\) có:
\(\widehat B\;chung\)
\(\widehat {BEF} = \widehat {BAC}\) (vì $EF\parallel AC$, cặp góc đồng vị bằng nhau)
\( \Rightarrow \Delta BFE \backsim \Delta BCA\;(g - g)\)
\(\begin{array}{l} \Rightarrow \dfrac{{BF}}{{BC}} = \dfrac{{FE}}{{CA}} \Leftrightarrow \dfrac{{BF}}{{BF + FN + NC}} = \dfrac{{FE}}{{CA}} \Leftrightarrow \dfrac{{1,32}}{{1,32 + 0,64 + 1,36}} = \dfrac{{1,65}}{{CA}}\\ \Rightarrow CA = 4,15\;m\end{array}\)
Vậy cây cao đúng bằng độ dài của đoạn CA hay cây cao 4,15 m.
Cho hình vẽ biết \(DE//BC\). Khẳng định nào sau đây là đúng?

-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\)
-
B.
\(AD.AE = AB.AC\)
-
C.
\(\dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC}}\)
-
D.
\(DE.AD = AB.BC\)
Đáp án : A
- Áp dụng định lý Talet, hệ quả định lý Ta-lét để tìm ra tỉ lệ thức phù hợp, từ đó thực hiện yêu cầu của bài toán.
Áp dụng hệ quả định lý Ta lét, ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow \) Đáp án A đúng.
+ Vì \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) nên \(AD.AC = AB.AE\)
\( \Rightarrow \) Đáp án B sai.
+ Ta có: \( \dfrac{{DE}}{{BC}}=\dfrac{{AD}}{{AB}} \ne \dfrac{{AD}}{{DB}}\) (hệ quả định lý Ta-lét)
\( \Rightarrow \) Đáp án C sai.
+ Ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow AD.BC = AB.DE\)
\( \Rightarrow \) Đáp án D sai.
Cho \(\Delta ABC\), đường phân giác góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,{\rm{ }}AD = 6{\rm{ }}cm.$ Tính $AC = $ ?
-
A.
$6{\rm{ }}cm$
-
B.
$9{\rm{ }}cm$
-
C.
$12{\rm{ }}cm$
-
D.
$15{\rm{ }}cm$
Đáp án : D
- Áp dụng tính chất đường phân giác để tính DC.
- Từ đó tính $AC=AD+DC$
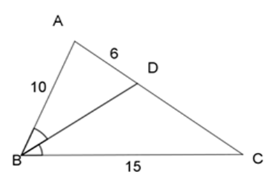
Áp dụng tính chất đường phân giác trong tam giác ABC, ta có: \(\dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CD}}\)
\( \Rightarrow \dfrac{{10}}{6} = \dfrac{{15}}{{CD}} \Leftrightarrow CD = \dfrac{{6.15}}{{10}} = 9\;cm\)
\( \Rightarrow AC = AD + DC = 6 + 9 = 15\;cm\)
Cho hình chữ nhật ABCD có \(AD = 8cm,\;AB = 9cm\). Các điểm $M,{\rm{ }}N$ trên đường chéo $BD$ sao cho $BM = MN = ND.$ Tính diện tích tam giác $CMN.$
-
A.
\(12c{m^2}\)
-
B.
\(24c{m^2}\)
-
C.
\(36c{m^2}\)
-
D.
\(6c{m^2}\)
Đáp án : A
+ Tính tỉ số diện tích tam giác \(CMN\) và tam giác \(BCD\)
+ Tính diện tích \(\Delta BCD\) suy ra diện tích tam giác \(CMN.\)
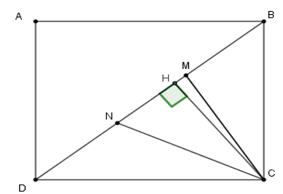
+ Ta có \(CD = AB = 9cm;BC = AD = 8cm\) nên \({S_{BCD}} = \dfrac{1}{2}BC.DC = \dfrac{1}{2}.8.9 = 36\,c{m^2}\)
+ Kẻ \(CH \bot BD\) tại \(H.\)
+ Ta có \({S_{BCD}} = \dfrac{1}{2}CH.BD;{S_{CMN}} = \dfrac{1}{2}CH.MN\) mà \(MN = \dfrac{1}{3}BD \Rightarrow {S_{CMN}} = \dfrac{1}{3}{S_{BCD}} = \dfrac{1}{3}.36 = 12\,c{m^2}\)
Hình chữ nhật có chiều dài tăng 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật
-
A.
không thay đổi
-
B.
tăng \(4\) lần
-
C.
giảm \(2\) lần
-
D.
tăng \(2\) lần
Đáp án : D
Sử dụng công thức tính diện tích hình chữ nhật bằng tích chiều dài nhân chiều rộng.
Theo công thức tính diện tích hình chữ nhật \(S = a.b\) thì diện tích hình chữ nhật tỉ lệ thuận với chiều dài và chiều rộng của nó
Nếu \(a' = 4a;\,\,\,b' = \dfrac{1}{2}b;\,\) thì \(S' = a'.b' = 4a.\dfrac{1}{2}b = \dfrac{4}{2}ab = 2S\)
Do đó diện tích mới bằng \(2\) lần diện tích đã cho.
Một đa giác lồi \(10\) cạnh thì có số đường chéo là:
-
A.
\(35\)
-
B.
\(30\)
-
C.
\(70\)
-
D.
\(27\)
Đáp án : A
Sử dụng công tính tính số đường chéo của hình n cạnh: \(\dfrac{{n\left( {n - 3} \right)}}{2}\)
Số đường chéo của hình \(10\) cạnh là: \(\dfrac{{10\left( {10 - 3} \right)}}{2} = 35\) đường.
Cho \(\Delta ABC\) vuông tại $A,$ đường cao $AH.$ Gọi $I$ và $K$ lần lượt là hình chiếu của $H$ lên $AB$ và $AC.$ Tam giác \(AIK\) đồng dạng với tam giác nào dưới đây?
-
A.
$ACB$
-
B.
$ABC$
-
C.
$CAB$
-
D.
\(BAC\)
Đáp án : A
+ Chứng minh tứ giác $AIHK$ là hình chữ nhật
+ Áp dụng các tính chất, định lý đã học và cách chứng minh đồng dạng của tam giác vuông để chứng minh yêu cầu của đề bài.
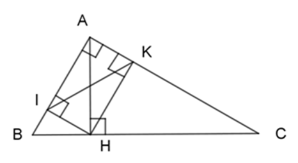
+) Có I, K lần lượt là hình chiếu của H lên AB và AC.
\( \Rightarrow \widehat {HIA} = \widehat {HKA} = {90^0}\)
Xét tứ giác AIHK có:
\(\widehat {IAK} = \widehat {HIA} = \widehat {HKA} = {90^0}\)
\( \Rightarrow \) Tứ giác AIHK là hình chữ nhật. (dhnb)
+) Xét \(\Delta AIK\) và \(\Delta IAH\) ta có:
\(AI\;chung\)
\(AK = IH\)(theo tính chất của hình chữ nhật)
\(AH = IK\;\) (theo tính chất của hình chữ nhật)
\( \Rightarrow \Delta AIK = \Delta IAH\;(c - c - c)\) (1)
Xét 2 tam giác vuông \(\Delta IAH\) và \(\Delta HAB\) có: \(\widehat A\) chung
\( \Rightarrow \Delta IAH \backsim \Delta HAB\;(g - g)\) (2)
Xét 2 tam giác vuông \(\Delta HAB\) và \(\Delta ACB\) có: \(\widehat B\) chung
\( \Rightarrow \)\(\Delta HAB \backsim \Delta ACB\;\;\left( {g - g} \right)\) (3)
Từ (1), (2) và (3) ta có: \(\Delta AIK \backsim \Delta ACB\)
Phương trình \(\left| {2x - 5} \right| = 1\) có nghiệm là:
-
A.
\(x = 3;x = 2\)
-
B.
\(x = \dfrac{5}{2};x = 2\)
-
C.
\(x = 1;x = 2\)
-
D.
$x = 0,5{\rm{ }};x = 1,5$
Đáp án : A
Bỏ dấu giá trị tuyệt đối bằng công thức: \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\)
Giải phương trình: \(\left| {2x - 5} \right| = 1\)
$TH1:\;2x - 5 \ge 0 \Leftrightarrow x \ge \dfrac{5}{2} \Rightarrow \left| {2x - 5} \right| = 2x - 5 = 1 \Leftrightarrow 2x = 6 \Leftrightarrow x = 3\;\;\left( {tm} \right)$
$TH2:\;2x - 5 < 0 \Leftrightarrow x < \dfrac{5}{2} \Rightarrow \left| {2x - 5} \right| = - 2x + 5 = 1 \Leftrightarrow 2x = 4 \Leftrightarrow x = 2\;\;\left( {tm} \right)$
Vậy phương trình có hai nghiệm \(x = 3\) và \(\;x = 2\).
Cho hình thang $ABCD\left( {AB//CD} \right),{\rm{ }}M$ là trung điểm của $AD,{\rm{ }}N$ là trung điểm của $BC.$ Gọi $I,{\rm{ }}K$ theo thứ tự là giao điểm của $MN$ với $BD,{\rm{ }}AC.$ Cho biết $AB = 6cm,{\rm{ }}CD = 14cm.$ Tính độ dài $MI,{\rm{ }}IK.$
-
A.
\(MI = 4cm;IK = 7cm.\)
-
B.
\(MI = 4cm;IK = 3cm.\)
-
C.
\(MI = 3cm;IK = 7cm.\)
-
D.
\(MI = 3cm;IK = 4cm.\)
Đáp án : D
+ Dựa vào tính chất đường trung bình của tam giác để tính độ dài $MI,{\rm{ }}MK.$ Từ đó suy ra độ dài $IK.$
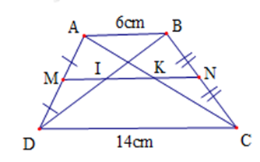
- Hình thang $ABCD$ có:
$\left. \begin{array}{l}{\rm{AM}} = {\rm{MD(gt)}}\\{\rm{BN}} = {\rm{NC (gt)}}\end{array} \right\} \Rightarrow $$MN$ là đường trung bình của hình thang $ABCD.$
\( \Rightarrow \) $MN//AB//CD$ (tính chất).
- Tam giác $ABD$ có: $\left. \begin{array}{l}{\rm{AM }} = {\rm{ MD}}\\MI//AB\end{array} \right\} \Rightarrow $$ID = IB$ (định lý đảo về đường trung bình của tam giác).
\( \Rightarrow \) $MI$ là đường trung bình của $\Delta ADB$ $ \Rightarrow MI = \dfrac{1}{2}AB = \dfrac{1}{2}.6 = 3(cm)$
- Tương tự tam giác \(ACD\) có: $AM = MD,{\rm{ }}MK//DC$ nên $AK = KC,$ hay ${\rm{ }}MK$ là đường trung bình của tam giác $ACD$, ta có:
$MK = \dfrac{1}{2}CD = \dfrac{1}{2}.14 = 7(cm)$
\( \Rightarrow \) $IK = MK - MI = 7 - 3 = 4\left( {cm} \right)$
Vậy \(MI = 3cm;IK = 4cm.\)
Cho tứ giác $ABCD,$ có \(\widehat A = {70^0},\) \(\widehat B = {120^0},\) \(\widehat D = {50^0},\) Số đo \(\widehat C\) là:
-
A.
\({100^0}\)
-
B.
\({105^0}\)
-
C.
\({120^0}\)
-
D.
\({115^0}\)
Đáp án : C
Dựa vào tính chất tổng các góc của một tứ giác bằng \({360^0}\).
Xét tứ giác \(ABCD\) ta có: $\hat A + \widehat B + \widehat C + \widehat D = {360^0}$
$\begin{array}{l} \Rightarrow \widehat C = {360^0} - \left( {\hat A + \widehat B + \widehat D} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - \left( {{{70}^0} + {{120}^0} + {{50}^0}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {240^0} = {120^0}.\end{array}$
Trong các tứ giác sau, tứ giác nào là hình có \(4\) trục đối xứng?
-
A.
Hình chữ nhật
-
B.
Hình vuông
-
C.
Hình bình hành
-
D.
Hình thoi
Đáp án : B
+ Dựa vào tính chất của các hình để suy ra trục đối xứng
+) Hình vuông là tứ giác có 4 trục đối xứng.
+) Hình chữ nhật có 2 trục đối xứng là hai đường trung trực của các cạnh.
+) Hình bình hành không có trục đối xứng.
+) Hình thoi có 2 trục đối xứng là 2 đường chéo.
Nghiệm của bất phương trình \(\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\) là
-
A.
$x < - 1$
-
B.
$x < 1$
-
C.
\(x > 1\)
-
D.
\(x > - 1\).
Đáp án : A
+) Với những bất phương trình chứa ẩn ở mẫu ta đặt điều kiện cho mẫu số khác 0.
+) Quy đồng mẫu thức các phân thức
+) Giải bất phương trình tìm điều kiện của $x$ sau đó đối chiếu với điều kiện để kết luận nghiệm của bất phương trình.
\(\begin{array}{l}\;\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\\ \Leftrightarrow \;\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\;\;\;\left( * \right)\end{array}\)
Điều kiện \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right..\)
\(\left( * \right) \Leftrightarrow \dfrac{{\left( {x + 4} \right)\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \dfrac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < \dfrac{{2{x^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)\( \Leftrightarrow \dfrac{{{x^2} + 3x - 4 + {x^2} + x - 2{x^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0\)
\( \Leftrightarrow \dfrac{{4x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0\)\( \Leftrightarrow \dfrac{{4\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0 \Leftrightarrow \dfrac{4}{{x + 1}} < 0\) mà \(4 > 0\) nên \(x + 1 < 0 \Leftrightarrow x < - 1.\)
Kết hợp với điều kiện ta có bất phương trình có nghiệm \(x < - 1\).
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
-
A.
\( - 16\)
-
B.
\( - 8\)
-
C.
\(16\)
-
D.
\(8\).
Đáp án : D
Vận dụng tính chất không âm của giá trị tuyệt đối dẫn đến phương pháp bất đẳng thức.
* Nhận xét: Tổng của các số không âm là một số không âm và tổng đó bằng 0 khi và chỉ khi các số hạng của tổng đồng thời bằng 0.
* Cách giải chung: \(\left| A \right| + \left| B \right| = 0\)
Bước1: Đánh giá: \(\left. \begin{array}{l}\left| A \right| \ge 0\\\left| B \right| \ge 0\end{array} \right\} \Rightarrow \left| A \right| + \left| B \right| \ge 0\)
Bước 2: Khẳng định: \(\left| A \right| + \left| B \right| = 0\)\( \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
\({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}\left| {x - 3y} \right| \ge 0\\\left| {y + 4} \right| \ge 0\end{array} \right\} \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} \ge 0\\ \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0 \Leftrightarrow \left\{ \begin{array}{l}x - 3y = 0\\y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3.( - 4) = 0\\y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 12\\y = - 4\end{array} \right.\end{array}\)
Vậy nghiệm của phương trình là $x = - 12$ và $y = - 4.$
Suy ra \(y - x = - 4 - \left( { - 12} \right) = 8.\)
Cho tam giác $ABC.$ Gọi $D,E,F\;$ theo thứ tự là trung điểm của $AB,BC,CA.$ Gọi $M,N,P,Q$ theo thứ tự là trung điểm của $AD,AF,EF,ED.\;$
$\Delta ABC$ có điều kiện gì thì $MNPQ$ là hình chữ nhật?
-
A.
$\Delta ABC$ cân tại $A$
-
B.
$\Delta ABC$ cân tại $B$
-
C.
$\Delta ABC$ cân tại $C$
-
D.
$\Delta ABC$ vuông tại $A$
Đáp án : A
Chứng minh \(MNPQ\) là hình bình hành
Dựa vào dấu hiệu nhận biết hình chữ nhật để suy ra điều kiện của tam giác \(ABC.\)
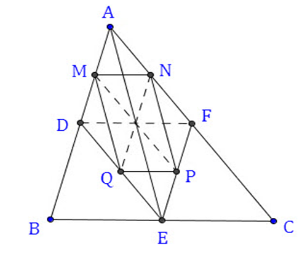
Xét $\Delta ADE$ có: $AM = DM;DQ = EQ$ nên $MQ$ là đường trung bình của $\Delta ADE$ . $ \Rightarrow MQ//AE;MQ = \dfrac{1}{2}AE$ Xét$\;\Delta AEF$ có: $AN = NF;FP = PE$ (giả thiết) nên $NP$ là đường trung bình của $\Delta AFE$. $ \Rightarrow NP//AE;NP = \dfrac{1}{2}AE$
Suy ra $MQ//NP $ ( cùng $//AE$ ) và $MQ = NP(= \dfrac{1}{2}AE)$ Tứ giác $MNPQ$ có: $MQ//NP$ và $MQ = NP$ nên là hình bình hành (dấu hiệu nhận biết).
Để $MNPQ$ là hình chữ nhật thì $MN \bot NP$ (1) Ta có: $NP//AE$ (chứng minh trên) (2). Ta lại có: $AM = MD,AN = NF$ (giả thiết) $ \Rightarrow MN//DF$. Mặt khác: $AD = DB,AF = FC$ (giả thiết) $ \Rightarrow DF//BC$
Vậy $MN//BC$ (3)
Từ (1), (2), (3) suy ra: $AE \bot BC$ . Mà $BE = EC$ (giả thiết) Do đó $\Delta ABC$ cân tại $A$ (do \(AE\) vừa là đường cao, vừa là đường trung tuyến).
Tính giá trị biểu thức \(P = \left( { - 4{x^3}{y^3} + {x^3}{y^4}} \right):2x{y^2} - xy\left( {2x - xy} \right)\) cho \(x = 1,y = \dfrac{{ - 1}}{2}\);
-
A.
\(P = - \dfrac{{19}}{8}\)
-
B.
\(P = \dfrac{{19}}{8}\)
-
C.
\(P = \dfrac{8}{{19}}\)
-
D.
\(P = \dfrac{9}{8}\)
Đáp án : B
- Rút gọn biểu thức đã cho, sau đó thay giá trị của biến vào biểu thức rút gọn để tìm ra giá trị của biểu thức.
\(\begin{array}{l}\,\,\,\,\,\,\,\,P = \left( { - 4{x^3}{y^3} + {x^3}{y^4}} \right):2x{y^2} - xy\left( {2x - xy} \right)\\ \Leftrightarrow P = \left( { - 4{x^3}{y^3}} \right):2x{y^2} + {x^3}{y^4}:2x{y^2} - xy.2x + xy.xy\\ \Leftrightarrow P = - 2{x^2}y + \dfrac{1}{2}{x^2}{y^2} - 2{x^2}y + {x^2}{y^2}\\ \Leftrightarrow P = \dfrac{3}{2}{x^2}{y^2} - 4{x^2}y\\ \Leftrightarrow P = {x^2}y\left( {\dfrac{3}{2}y - 4} \right)\end{array}\)
Tại \(x = 1,y = \dfrac{{ - 1}}{2}\), ta có: \(P = {1^2}.\left( {\dfrac{{ - 1}}{2}} \right)\left( {\dfrac{3}{2}\left( {\dfrac{{ - 1}}{2}} \right) - 4} \right) = \left( {\dfrac{{ - 1}}{2}} \right)\left( {\dfrac{{ - 3}}{4} - 4} \right) = \left( {\dfrac{{ - 1}}{2}} \right)\left( {\dfrac{{ - 19}}{4}} \right) = \dfrac{{19}}{8}\)
Thực hiện phép tính \(A = \left( {6{x^3} - 5{x^2} + 4x - 1} \right):\left( {2{x^2} - x + 1} \right)\) ta được
-
A.
\(3x - 1\)
-
B.
\(3x + 1\)
-
C.
\(3x\)
-
D.
\(3\)
Đáp án : A
Đặt tính theo hàng dọc rồi thực hiện phép chia để tìm thương
\(\left( {6{x^3} - 5{x^2} + 4x - 1} \right):\left( {2{x^2} - x + 1} \right)\)
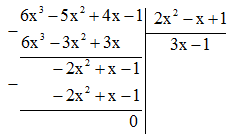
\(\left( {6{x^3} - 5{x^2} + 4x - 1} \right):\left( {2{x^2} - x + 1} \right) = 3x - 1.\)
Phân tích đa thức sau thành nhân tử: \({x^3} - 5x + 4\) ta được
-
A.
\(\left( {x + 1} \right)\left( {{x^2} + x - 4} \right)\)
-
B.
\(\left( {x - 1} \right)\left( {{x^2} - x - 4} \right)\)
-
C.
\(\left( {x - 1} \right)\left( {{x^2} + x - 4} \right)\)
-
D.
\(\left( {x - 1} \right)\left( {{x^2} + x + 4} \right)\)
Đáp án : C
- Tách 1 hạng tử thành nhiều hạng tử hoặc thêm, bớt cùng một hạng tử làm xuất hiện nhân tử chung hoặc các hằng đẳng thức.
- Đặt nhân tử chung, dùng các hằng đẳng thức đáng nhớ hoặc nhóm các hạng tử một cách thích hợp nhằm xuất hiện hằng đẳng thức hoặc nhân tử chung mới.
\(\begin{array}{l}\,\,\,\,\,{x^3} - 5x + 4\\ = {x^3} - x - 4x + 4\\ = x\left( {{x^2} - 1} \right) - 4\left( {x - 1} \right)\\ = x\left( {x - 1} \right)\left( {x + 1} \right) - 4\left( {x - 1} \right)\\ = \left( {x - 1} \right)\left[ {x\left( {x + 1} \right) - 4} \right]\\ = \left( {x - 1} \right)\left( {{x^2} + x - 4} \right).\end{array}\)
Rút gọn đa thức \(16{x^2} - 4x + \dfrac{1}{4}\) ta được kết quả nào sau đây?
-
A.
\({\left( {4x - \dfrac{1}{2}} \right)^2}\)
-
B.
\({\left( {x - \dfrac{1}{2}} \right)^2}\)
-
C.
\({\left( {4x + \dfrac{1}{2}} \right)^2}\)
-
D.
\({\left( {x + \dfrac{1}{2}} \right)^2}\)
Đáp án : A
Sử dụng hằng đẳng thức \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
\(16{x^2} - 4x + \dfrac{1}{4} = {\left( {4x} \right)^2} - 2.4x.\dfrac{1}{2} + {\left( {\dfrac{1}{2}} \right)^2} = {\left( {4x - \dfrac{1}{2}} \right)^2}\)
Tìm \(x\) biết \(\left( {x + 2} \right)(x + 3) - \left( {x - 2} \right)\left( {x + 5} \right) = 6\)
-
A.
\(x = - 5.\)
-
B.
\(x = 5.\)
-
C.
\(x = - 10.\)
-
D.
\(x = - 1.\)
Đáp án : A
Biến đổi vế trái bằng cách sử dụng quy tắc nhân đa thức với đa thức rồi cộng trừ các hạng tử đồng dạng
Từ đó tìm \(x.\)
\(\begin{array}{l}\left( {x + 2} \right)(x + 3) - \left( {x - 2} \right)\left( {x + 5} \right) = 6\\ \Leftrightarrow x.x + 3.x + 2.x + 2.3 - x.x - 5.x + 2.x + 2.5 = 6\\ \Leftrightarrow {x^2} + 3x + 2x + 6 - {x^2} - 5x + 2x + 10 = 6\\ \Leftrightarrow 2x + 16 = 6\\ \Leftrightarrow 2x = - 10\\ \Leftrightarrow x = - 5\end{array}\)
Vậy \(x = - 5.\)
Cho $Q = \left( {\dfrac{{{x^2} + 3x}}{{{x^3} + 3{x^2} + 9x + 27}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^3} - 3{x^2} + 9x - 27}}} \right).$ Rút gọn $Q$ ta được.
-
A.
\(Q = \dfrac{1}{{{x^2} + 9}}\)
-
B.
\(Q = \dfrac{{x - 3}}{{x + 3}}\)
-
C.
\(Q = \dfrac{1}{{x - 3}}\)
-
D.
\(Q = \dfrac{{x + 3}}{{x - 3}}\)
Đáp án : D
- Tìm điều kiện để phân thức có nghĩa
- Phân tích các mẫu thức thành nhân tử
- Qui đồng các phân thức và thu gọn biểu thức
$Q = \left( {\dfrac{{{x^3} + 3x}}{{{x^3} + 3{x^2} + 9x + 27}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^3} - 3{x^2} + 9x - 27}}} \right)$ (ĐK: \(x \ne \pm 3\))
$\begin{array}{l}Q = \left( {\dfrac{{{x^2} + 3x}}{{{x^3} + 3{x^2} + 9x + 27}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^3} - 3{x^2} + 9x - 27}}} \right)\\\,\,\,\,\, = \left( {\dfrac{{{x^2} + 3x}}{{{x^2}(x + 3) + 9(x + 3)}} + \dfrac{3}{{{x^2} + 9}}} \right):\left( {\dfrac{1}{{x - 3}} - \dfrac{{6x}}{{{x^2}(x - 3) + 9(x - 3)}}} \right)\\\,\,\,\,\, = \dfrac{{{x^2} + 3x + 3x + 9}}{{\left( {{x^2} + 9} \right)\left( {x + 3} \right)}}:\dfrac{{{x^2} + 9 - 6x}}{{\left( {x - 3} \right)\left( {{x^2} + 9} \right)}}\\\,\,\,\,\,\, = \dfrac{{{{(x + 3)}^2}}}{{({x^2} + 9)(x + 3)}}.\dfrac{{(x - 3)({x^2} + 9)}}{{{{(x - 3)}^2}}}\\\,\,\,\,\,\, = \dfrac{{x + 3}}{{x - 3}}.\end{array}$
Rút gọn biểu thức \(\dfrac{{{x^4} + 4{x^2} + 5}}{{5{x^3} + 5}}\,\, \cdot \,\,\dfrac{{2x}}{{{x^2} + 4}}\,\, \cdot \,\,\dfrac{{3{x^3} + 3}}{{{x^4} + 4{x^2} + 5}}\) ta được:
-
A.
\(\dfrac{{2x}}{{5({x^2} + 4)}}\)
-
B.
\(\dfrac{{6x}}{{5({x^2} + 4)}}\)
-
C.
\(\dfrac{{3x}}{{5({x^2} + 4)}}\)
-
D.
\(\dfrac{x}{{5({x^2} + 4)}}\)
Đáp án : B
Ta biến đổi để rút gọn các phân thức rồi thực hiện phép tính nhân phân thức.
\(\dfrac{{{x^4} + 4{x^2} + 5}}{{5{x^3} + 5}}\,\, \cdot \,\,\dfrac{{2x}}{{{x^2} + 4}}\,\, \cdot \,\,\dfrac{{3{x^3} + 3}}{{{x^4} + 4{x^2} + 5}} = \dfrac{{{x^4} + 4{x^2} + 5}}{{5({x^3} + 1)}}\,\, \cdot \,\,\dfrac{{2x}}{{{x^2} + 4}}\,\, \cdot \,\,\dfrac{{3({x^3} + 1)}}{{{x^4} + 4{x^2} + 5}} = \dfrac{{6x}}{{5({x^2} + 4)}}.\)
Thực hiện phép tính sau: $\dfrac{{{x^3}}}{{{x^2} + 1}} + \dfrac{x}{{{x^2} + 1}}$
-
A.
$ - x$
-
B.
$2x$
-
C.
$\dfrac{x}{2}$
-
D.
$x$
Đáp án : D
Sử dụng kiến thức cộng 2 phân thức cùng mẫu, phân tích đa thức thành nhân tử và rút gọn.
Ta có $\dfrac{{{x^3}}}{{{x^2} + 1}} + \dfrac{x}{{{x^2} + 1}} = \dfrac{{{x^3} + x}}{{{x^2} + 1}} = \dfrac{{x({x^2} + 1)}}{{{x^2} + 1}} = x.$
Kết quả của phép tính $\dfrac{1}{x} + \dfrac{1}{{x(x + 1)}} + ... + \dfrac{1}{{(x + 9)(x + 10)}}$ là:
-
A.
$\dfrac{{x + 20}}{{x(x + 10)}}$
-
B.
$\dfrac{{x + 9}}{{x + 10}}$
-
C.
$\dfrac{1}{{x + 10}}$
-
D.
$\dfrac{1}{{x(x + 1)...(x + 10)}}$
Đáp án : A
Sử dụng kiến thức $\dfrac{1}{{x(x + 1)}} = \dfrac{1}{x} - \dfrac{1}{{x + 1}}$; cộng 2 phân thức khác mẫu.
Ta có : $\dfrac{1}{x} + \dfrac{1}{{x(x + 1)}} + ... + \dfrac{1}{{(x + 9)(x + 10)}}$
$\begin{array}{l} = \dfrac{1}{x} + \dfrac{1}{x} - \dfrac{1}{{x + 1}} + \dfrac{1}{{x + 1}} - \dfrac{1}{{x + 2}}... + \dfrac{1}{{x + 9}} - \dfrac{1}{{x + 10}}\\ = \dfrac{1}{x} + \dfrac{1}{x} + 0 + ... + 0 - \dfrac{1}{{x + 10}}\\ = \dfrac{2}{x} - \dfrac{1}{{x + 10}}\\ = \dfrac{{2x + 20 - x}}{{x(x + 10)}} = \dfrac{{x + 20}}{{x(x + 10)}}.\end{array}$
Tổng các nghiệm của phương trình: \(\dfrac{1}{{{x^2} + 4x + 3}} + \dfrac{1}{{{x^2} + 8x + 15}} + \dfrac{1}{{{x^2} + 12x + 35}} + \dfrac{1}{{{x^2} + 16x + 63}} = \dfrac{1}{5}\) là
-
A.
\(10\)
-
B.
\( - 10\)
-
C.
\( - 11\)
-
D.
\(12\)
Đáp án : B
Phân tích mẫu thức thành nhân tử rồi sử dụng phương pháp tách hạng tử để giải
\(\dfrac{1}{{\left( {x + a} \right)\left( {x + b} \right)}} = \dfrac{1}{{b - a}}\left( {\dfrac{1}{{x + a}} - \dfrac{1}{{x + b}}} \right),a \ne b\) . Sau đó, làm theo các bước giải phương trình chứa ẩn ở mẫu.
Phân tích các mẫu thành nhân tử sau đó nhân cả 2 vế của phương trình với 2 ta được:
\(\dfrac{1}{{\left( {x + 1} \right)\left( {x + 3} \right)}} + \dfrac{1}{{\left( {x + 3} \right)\left( {x + 5} \right)}} + \dfrac{1}{{\left( {x + 5} \right)\left( {x + 7} \right)}} + \dfrac{1}{{\left( {x + 7} \right)\left( {x + 9} \right)}} = \dfrac{1}{5}\\\dfrac{2}{{\left( {x + 1} \right)\left( {x + 3} \right)}} + \dfrac{2}{{\left( {x + 3} \right)\left( {x + 5} \right)}} + \dfrac{2}{{\left( {x + 5} \right)\left( {x + 7} \right)}} + \dfrac{2}{{\left( {x + 7} \right)\left( {x + 9} \right)}} = \dfrac{2}{5}\)
ĐKXĐ: $x \ne \left\{ { - 1; - 3; - 5; - 7; - 9} \right\}$ .
Khi đó:
\(\dfrac{1}{{x + 1}} - \dfrac{1}{{x + 3}} + \dfrac{1}{{x + 3}} - \dfrac{1}{{x + 5}} + \dfrac{1}{{x + 5}} - \dfrac{1}{{x + 7}} + \dfrac{1}{{x + 7}} - \dfrac{1}{{x + 9}} = \dfrac{2}{5}\\\dfrac{1}{{x + 1}} - \dfrac{1}{{x + 9}} = \dfrac{2}{5}\\\dfrac{{1\left( {x + 9} \right) - 1\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x + 9} \right)}} = \dfrac{{2\left( {x + 1} \right)\left( {x + 9} \right)}}{{5\left( {x + 1} \right)\left( {x + 9} \right)}}\\5\left[ {x + 9 - \left( {x + 1} \right)} \right] = 2\left( {x + 1} \right)\left( {x + 9} \right)\\5\left( {x + 9 - x - 1} \right) = 2{x^2} + 20x + 18\\2{x^2} + 20x - 22 = 0 \\{x^2} + 10x - 11 = 0\\{x^2} - x + 11x - 11 = 0 \\\left( {x - 1} \right)\left( {x + 11} \right) = 0\)
Suy ra \(x - 1 = 0\) hoặc \(x + 11 = 0\),
tức là \(x = 1(tm)\) hoặc \(x = - 11(tm)\)
Vậy tổng các nghiệm của phương trình là \(1 + \left( { - 11} \right) = - 10.\)
Giải phương trình: \(2x\left( {x - 5} \right) + 21 = x\left( {2x + 1} \right) - 12\) ta được nghiệm \({x_0}.\) Chọn câu đúng.
-
A.
\({x_0} = 4\)
-
B.
\({x_0} < 4\)
-
C.
\({x_0} > 4\)
-
D.
\({x_0} > 5\)
Đáp án : B
Sử dụng quy tắc nhân, quy tắc chuyển vế để đưa phương trình về dạng phương trình bậc nhất một ẩn rồi giải.
\(\begin{array}{l}2x\left( {x - 5} \right) + 21 = x\left( {2x + 1} \right) – 12\\ 2{x^2} - 10x + 21 = 2{x^2} + x - 12\\2{x^2} - 10x - 2{x^2} - x = - 12 - 21\\- 11x = - 33\\ = 3\end{array}\)
Vậy phương trình có tập nghiệm là \(S = \left\{ 3 \right\}\) hay \({x_0} = 3 < 4.\)
Phương trình \(\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} = 1\) có nghiệm là
-
A.
\(x = - \dfrac{1}{2}\)
-
B.
\(x = \dfrac{5}{2}\)
-
C.
\(x = \dfrac{1}{2}\)
-
D.
\(x = - \dfrac{5}{2}\)
Đáp án : D
+ Tìm ĐKXĐ của phương trình.
+ Quy đồng mẫu rồi khử mẫu.
+ Giải phương trình vừa nhận được.
+ Đối chiếu điều kiện rồi kết luận nghiệm.
ĐKXĐ: \(x \ne 2;x \ne 5\)
\(\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} = 1\,\\\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} - 1 = 0\\\dfrac{{x\left( {x - 2} \right) - 3\left( {x - 5} \right) - 1\left( {x - 2} \right)\left( {x - 5} \right)}}{{\left( {x - 2} \right)\left( {x - 5} \right)}} = 0\\x\left( {x - 2} \right) - 3\left( {x - 5} \right) - 1\left( {x - 2} \right)\left( {x - 5} \right) = 0\\{x^2} - 2x - 3x + 15 - {x^2} + 7x - 10 = 0\\2x + 5 = 0\\2x = - 5 \\x = - \dfrac{5}{2}\left( {tmdk} \right).\)
Hình vẽ dưới đây là biểu diễn tập nghiệm của bất phương trình nào?
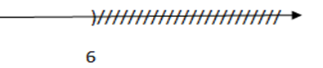
-
A.
$x - 1 \ge 5$
-
B.
$x + 1 \le 7$
-
C.
$x + 3 < 9$
-
D.
$x + 1 > 7$.
Đáp án : C
Tìm nghiệm của mỗi phương trình rồi so sánh với đề bài.
Theo đề bài thì trục số biểu diễn tập nghiệm \(x < 6.\)
Ta có
+) Đáp án A: $x - 1 \ge 5 \Leftrightarrow x \ge 6$ loại vì tập nghiệm là \(x < 6.\)
+) Đáp án B: \(x + 1 \le 7 \Leftrightarrow x \le 6\) loại vì tập nghiệm là \(x < 6.\)
+) Đáp án C: \(x + 3 < 9 \Leftrightarrow x < 6\) thỏa mãn vì tập nghiệm là \(x < 6.\)
+) Đáp án D: \(x + 1 > 7 \Leftrightarrow x > 6\) loại vì tập nghiệm là \(x < 6.\)