Giải bài 1.11 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức
Trong Hình 1.31, BAM và CAN là các tam giác vuông cân tại A. Hãy chỉ ra một phép quay biến tam giác ABC thành tam giác AMN.
Đề bài
Trong Hình 1.31, BAM và CAN là các tam giác vuông cân tại A. Hãy chỉ ra một phép quay biến tam giác ABC thành tam giác AMN.
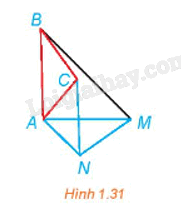
Phương pháp giải - Xem chi tiết
Ta cần tìm tâm và góc quay: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết
Tam giác BAM vuông cân tại A nên AB = AM và \(\widehat {BAM} = 90^\circ \). Do đó, ta có phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến điểm A thành điểm A, biến điểm B thành điểm M (1).
Tam giác ACN vuông cân tại A nên AC = AN và \(\widehat {CAN} = 90^\circ \). Do đó, ta có phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến điểm C thành điểm N (2).
Từ (1) và (2) suy ra phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến tam giác ABC thành tam giác AMN.