Giải bài 1.13 trang 14 sách bài tập toán 12 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = - {x^3} + 3{x^2} + 2); b) (y = frac{{{x^2}}}{{{x^2} + 2}}).
Đề bài
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = - {x^3} + 3{x^2} + 2\);
b) \(y = \frac{{{x^2}}}{{{x^2} + 2}}\).
Phương pháp giải - Xem chi tiết
- Tìm tập xác định của hàm số.
- Tính đạo hàm, tìm các điểm mà tại đó đạo hàm bằng \(0\) hoặc đạo hàm không tồn tại.
- Lập bảng biến thiên của hàm số.
- Từ bảng biến thiên suy ra giá trị lớn nhất, nhỏ nhất (nếu có).
Lời giải chi tiết
a) Tập xác định: \(\mathbb{R}\)
Ta có \(y' = - 3{x^2} + 6x\). Khi đó \(y' = 0 \Leftrightarrow - 3{x^2} + 6x = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\).
Lập bảng biến thiên của hàm số:
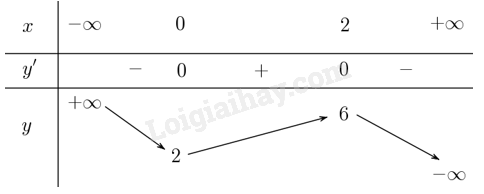
Từ bảng biến thiên thấy hàm số không có cả giá trị lớn nhất và giá trị nhỏ nhất.
b) Tập xác định: \(\mathbb{R}\)
Ta có \(y' = \frac{{1 \cdot \left( {{x^2} + 2} \right) - x \cdot 2x}}{{{{\left( {{x^2} + 2} \right)}^2}}} = \frac{{ - {x^2} + 2}}{{{{\left( {{x^2} + 2} \right)}^2}}}\).
Khi đó \(y' = 0 \Leftrightarrow \frac{{ - {x^2} + 2}}{{{{\left( {{x^2} + 2} \right)}^2}}} = 0 \Leftrightarrow - {x^2} + 2 = 0 \Leftrightarrow x = - \sqrt 2 \) hoặc \(x = \sqrt 2 \).
Lập bảng biến thiên của hàm số:
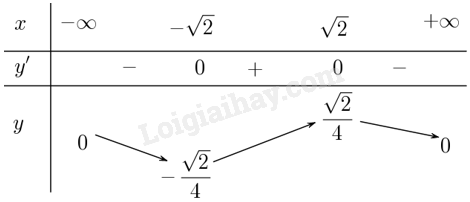
Từ bảng biến thiên, ta có: \(\mathop {\min }\limits_\mathbb{R} y = y\left( { - \sqrt 2 } \right) = \frac{{ - \sqrt 2 }}{4}\); \(\mathop {\max }\limits_\mathbb{R} y = y\left( {\sqrt 2 } \right) = \frac{{\sqrt 2 }}{4}\).