Giải bài 1. 2 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1 — Không quảng cáo

Đề bài

Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) \(3x - 2y = 5\);

b) \(0x + 2y = 4\);

c) \(2x + 0y =  - 3\).

Lời giải chi tiết

a) Vì \(3x - 2y = 5\) nên \(y = \frac{{3x - 5}}{2}\).

Do đó, nghiệm tổng quát của phương trình là \(\left( {x;\frac{{3x - 5}}{2}} \right)\) với \(x \in \mathbb{R}\) tùy ý.

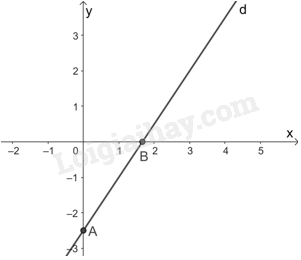
Đường thẳng d: \(3x - 2y = 5\) đi qua hai điểm A(0; -2,5) và \(B\left( {\frac{5}{3};0} \right)\).

Do đó, hình biểu diễn tất cả các nghiệm của mỗi phương trình đã cho là:

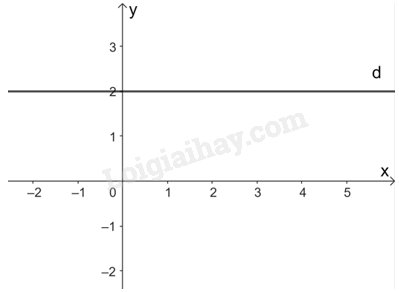
b) Vì \(0x + 2y = 4\) nên \(y = 2\).

Do đó, nghiệm tổng quát của phương trình là: \(\left( {x;2} \right)\) với \(x \in \mathbb{R}\) tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm (0; 2).

Đó là đường thẳng d: \(y = 2\).

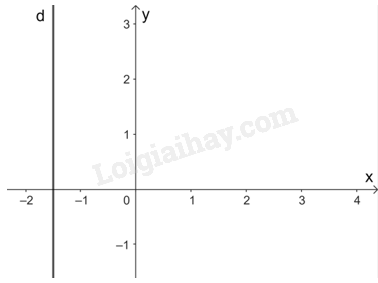
c) Vì \(2x + 0y =  - 3\) nên \(x =  - 1,5\).

Do đó, nghiệm tổng quát của phương trình là \(\left( { - 1,5;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm (-1,5; 0).

Đó là đường thẳng d: \(x =  - 1,5\).