Giải bài 1.6 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho các cặp số (-2; 2), (1; 1), (4; 1), (8; -2) và hai phương trình: (x + 3y = 4); (1) (2x - 5y = - 3). (2) a) Những cặp số nào là nghiệm của phương trình (1)? b) Cặp số nào là nghiệm của hệ gồm hai phương trình (1) và phương trình (2)? c) Vẽ hai đường thẳng (d:x + 3y = 4) và (d':2x - 5y = - 3) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Đề bài
Cho các cặp số (-2; 2), (1; 1), (4; 1), (8; -2) và hai phương trình:
\(x + 3y = 4\); (1)
\(2x - 5y = - 3\). (2)
a) Những cặp số nào là nghiệm của phương trình (1)?
b) Cặp số nào là nghiệm của hệ gồm hai phương trình (1) và phương trình (2)?
c) Vẽ hai đường thẳng \(d:x + 3y = 4\) và \(d':2x - 5y = - 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Phương pháp giải - Xem chi tiết
a) Nếu tại \(x = {x_0}\) và \(y = {y_0}\) ta có \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là nghiệm của phương trình bậc nhất hai ẩn \(ax + by = c\).
b) Mỗi cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).
Lời giải chi tiết
a) Với \(x = - 2,y = 2\) ta có: \( - 2 + 3.2 = 4\) nên (-2; 2) là nghiệm của phương trình \(x + 3y = 4\).
Với \(x = 1,y = 1\) ta có: \(1 + 3.1 = 4\) nên (1; 1) là nghiệm của phương trình \(x + 3y = 4\).
Với \(x = 4,y = 1\) ta có: \(4 + 3.1 = 7 \ne 4\) nên (4; 1) không là nghiệm của phương trình \(x + 3y = 4\).
Với \(x = 8,y = - 2\) ta có: \(8 + 3.\left( { - 2} \right) = 2 \ne 4\) nên (8; -2) là nghiệm của phương trình \(x + 3y = 4\).
Vậy cặp số là nghiệm của phương trình (1) là (-2; 2), (1; 1).
b) Với \(x = 1,y = 1\) ta có: \(2.1 - 5.1 = - 3\) nên (1; 1) là nghiệm của phương trình \(2x - 5y = - 3\).
Vậy cặp số (1; 1) là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2).
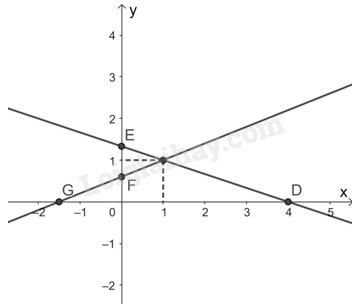
c) Đường thẳng \(x + 3y = 4\) đi qua hai điểm \(E\left( {0;\frac{4}{3}} \right)\) và \(D\left( {4;0} \right)\).
Đường thẳng \(2x - 5y = - 3\) đi qua hai điểm \(F\left( {0;\frac{3}{5}} \right)\) và \(G\left( {\frac{{ - 3}}{2};0} \right)\).
Do đó, đồ thị hàm số của hai đường thẳng \(x + 3y = 4\) và \(2x - 5y = - 3\) trên cùng một mặt phẳng tọa độ là: