Giải bài 1. 8 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1 — Không quảng cáo

Đề bài

Bằng cách vẽ các đường thẳng thích hợp trên cùng một mặt phẳng tọa độ, hãy tìm nghiệm của mỗi hệ phương trình sau:

a) $\left\{ \begin{array}{l}2x =  - 4\\3x - y = 5\end{array} \right.$;

b) $\left\{ \begin{array}{l}x - 2y = 4\\2y =  - 3\end{array} \right.$.

Lời giải chi tiết

a) Đường thẳng (d): $2x =  - 4$ là đường thẳng song song với trục tung và cắt trục hoành tại điểm có hoành độ bằng -2.

Đường thẳng (d’): $3x - y = 5$ đi qua hai điểm (0; -5) và $\left( {\frac{5}{3};0} \right)$.

Vẽ hai đường thẳng (d) và (d’) trên cùng mặt phẳng tọa độ:

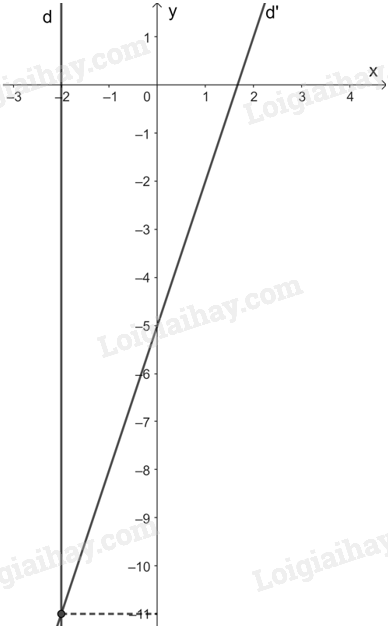
Từ đồ thị ta thấy, điểm (-2; -11) là nghiệm của hệ phương trình đã cho.

b) Đường thẳng (d): $x - 2y = 4$ đi qua hai điểm A(0; -2) và B(4; 0).

Đường thẳng (d’): $2y =  - 3$ là đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ $y =  - 1,5$.

Vẽ hai đường thẳng (d) và (d’) trên cùng mặt phẳng tọa độ:

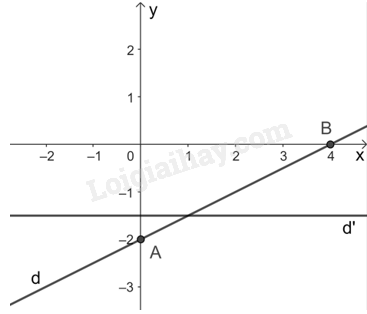
Từ đồ thị ta thấy, điểm (1; -1,5) là nghiệm của hệ phương trình đã cho.