Giải bài 1. 28 trang 20 sách bài tập toán 12 - Kết nối tri thức — Không quảng cáo

Đề bài

Cho hàm số $y = f\left( x \right) = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}}$ có đồ thị như hình vẽ sau:

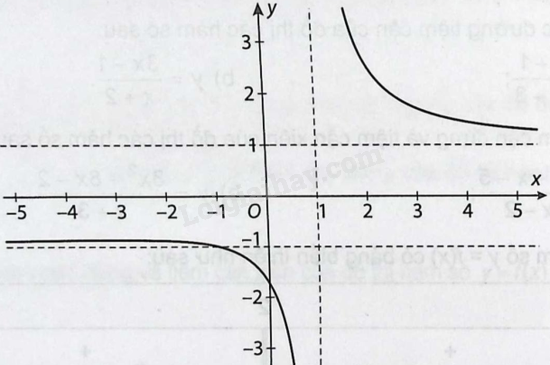
Hãy tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.

Lời giải chi tiết

Ta có $\mathop {\lim }\limits_{x \to {1^ + }} y = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}} =  + \infty$; $\mathop {\lim }\limits_{x \to {1^ - }} y = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}} =  - \infty$. Do đó đường thẳng $x = 1$ là tiệm cận đứng của đồ thị hàm số.

$\mathop {\lim }\limits_{x \to  + \infty } y = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}} = 1$. Do đó đường thẳng $y = 1$ là tiệm cận ngang của đồ thị hàm số.

$\mathop {\lim }\limits_{x \to  - \infty } y = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}} =  - 1$. Do đó đường thẳng $y =  - 1$ là tiệm cận ngang của đồ thị hàm số