Giải bài 1.35 trang 25 sách bài tập toán 12 - Kết nối tri thức
Gia tốc \(a\left( t \right)\) của một vật chuyển động, \(t\) tính theo giây, từ giây thứ nhất đến giây thứ \(5\) là một hàm liên tục có đồ thị như sau: a) Lập bảng biến thiên của hàm vận tốc \(y = v\left( t \right)\) của vật, với \(t \in \left[ {1;5} \right]\). b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất?
Đề bài
Gia tốc \(a\left( t \right)\) của một vật chuyển động, \(t\) tính theo giây, từ giây thứ nhất đến giây thứ \(5\) là một hàm liên tục có đồ thị như sau:
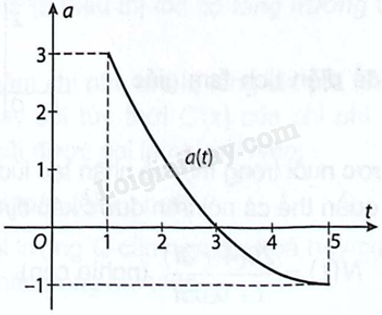
a) Lập bảng biến thiên của hàm vận tốc \(y = v\left( t \right)\) của vật, với \(t \in \left[ {1;5} \right]\).
b) Tại thời điểm nào vật chuyển động với vận tốc lớn nhất?
Phương pháp giải - Xem chi tiết
Ý a:
+ \(a\left( t \right) = v'\left( t \right)\). Từ đồ thị xét dấu \(a\left( t \right)\) trên khoảng \(t \in \left[ {1;5} \right]\)
+ Lập bảng biến thiên của \(v\left( t \right)\).
Ý b: Từ bảng biến thiên suy ra được giá trị lớn nhất của vận tốc đạt được tại thời điểm nào.
Lời giải chi tiết
a) Ta có \(a\left( t \right) = v'\left( t \right)\).
Từ đồ thị ta có \(a\left( t \right) = 0 \Leftrightarrow t = 3\).
Ta thấy \(a\left( t \right) > 0\) với mọi \(t \in \left( {1;3} \right)\), \(a\left( t \right) < 0\) với mọi \(t \in \left( {3;5} \right)\).
Lập bảng biến thiên
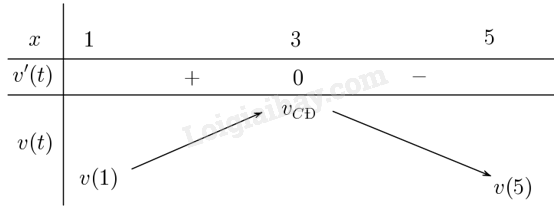
b) Từ bảng biến thiên suy ra vận tốc lớn nhất đạt tại giây thứ \(3\) (\(t = 3\)).