Giải bài 1 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2 — Không quảng cáo

Đề bài

Cho tứ diện ABCD có tam giác BCD vuông cân tại B và \(AB \bot \left( {BCD} \right)\). Cho biết \(BC = a\sqrt 2 ,AB = \frac{a}{{\sqrt 3 }}\). Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD).

Lời giải chi tiết

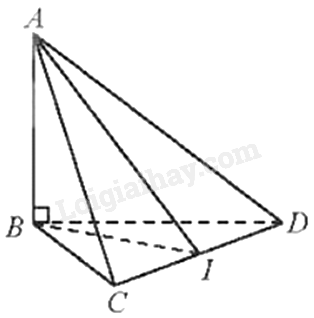
Gọi I là trung điểm của CD.

Tam giác BCD vuông cân tại B nên BI là đường trung tuyến đồng thời là đường cao.

Do đó, \(BI \bot CD\).

Tam giác BCD vuông cân tại B nên \(BC = BD = a\sqrt 2 \)

Vì \(AB \bot \left( {BCD} \right),BD \subset \left( {BCD} \right) \Rightarrow AB \bot BD\). Do đó, tam giác ABD vuông tại B.

Áp dụng định lí Pythagore vào tam giác ABD vuông tại B có:

\(AD = \sqrt {A{B^2} + B{D^2}}  = \sqrt {{{\left( {\frac{a}{{\sqrt 3 }}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}}  = \frac{{a\sqrt {21} }}{3}\)

Vì \(AB \bot \left( {BCD} \right),BC \subset \left( {BCD} \right) \Rightarrow AB \bot BC\). Do đó, tam giác ABC vuông tại B.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:

\(AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{{\left( {\frac{a}{{\sqrt 3 }}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}}  = \frac{{a\sqrt {21} }}{3}\)

Do đó, \(AC = AD\) nên tam giác ACD cân tại A.

Nên AI là đường trung tuyến đồng thời là đường cao. Suy ra, \(AI \bot CD\).

Ta có: CD là giao tuyến của hai mặt phẳng (BCD) và (ACD)\(BI \bot CD,AI \bot CD,BI \subset \left( {BCD} \right),AI \subset \left( {ACD} \right)\). Nên \(\left( {\left( {ACD} \right),\left( {BCD} \right)} \right) = \left( {AI,BI} \right) = \widehat {AIB}\)

Áp dụng định lí Pythagore vào tam giác BCD vuông tai B có: \(CD = \sqrt {B{C^2} + B{D^2}}  = 2a\)

Tam giác BCD vuông cân tại B nên \(BI = \frac{{CD}}{2} = a\)

Vì \(AB \bot \left( {BCD} \right),BI \subset \left( {BCD} \right) \Rightarrow AB \bot BI\). Do đó, tam giác ABI vuông tại B.

Do đó, \(\tan \widehat {AIB} = \frac{{AB}}{{BI}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {AIB} = {30^0}\)