Giải bài 12 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
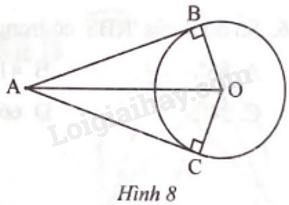
Cho AB và AC là hai tiếp tuyến tiếp xúc với đường tròn (O; R) lần lượt tại hai tiếp điểm B và C (Hình 8). a) AB = AO. b) Tia AO là tia phân giác của (widehat {BAC}). c) Tia OA là tai phân giác của (widehat {BOC}) d) OA = OB = R.
Đề bài
Chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Cho AB và AC là hai tiếp tuyến tiếp xúc với đường tròn (O; R) lần lượt tại hai tiếp điểm B và C (Hình 8).
a) AB = AO.
b) Tia AO là tia phân giác của \(\widehat {BAC}\) .
c) Tia OA là tai phân giác của \(\widehat {BOC}\)
d) OA = OB = R.
Phương pháp giải - Xem chi tiết
Dựa vào: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
*Điểm đó cách đều hai tiếp điểm
*Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
* Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Đường tròn tâm O bán kính R (R > 0) là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.
Lời giải chi tiết
a) Sai.
b) Đúng vì AB và AC là hai tiếp tuyến cắt nhau tại A và tia AO đi qua tâm O.
c) Đúng vì tia kẻ từ tâm O đi qua điểm A là giao điểm của hai tiếp tuyến AB và AC.
d) Sai.