Giải bài 12 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác nhọn ABC và điểm D nằm giữa B và C. Gọi E và F lần lượt là chân đường vuông góc hạ từ D xuống AB và AC. a) Gọi I và J lần lượt là tâm đường tròn ngoại tiếp tam giác EBD và tam giác FDC. Chứng minh rằng hai đường tròn (I) và (J) tiếp xúc ngoài với nhau. b) Giả sử M là một điểm tùy ý khác F, nằm giữa A và C; gọi K là tâm đường tròn ngoại tiếp tam giác MDC. Chứng minh rằng hai đường tròn (I) và (K) cắt nhau.
Đề bài
Cho tam giác nhọn ABC và điểm D nằm giữa B và C. Gọi E và F lần lượt là chân đường vuông góc hạ từ D xuống AB và AC.
a) Gọi I và J lần lượt là tâm đường tròn ngoại tiếp tam giác EBD và tam giác FDC. Chứng minh rằng hai đường tròn (I) và (J) tiếp xúc ngoài với nhau.
b) Giả sử M là một điểm tùy ý khác F, nằm giữa A và C; gọi K là tâm đường tròn ngoại tiếp tam giác MDC. Chứng minh rằng hai đường tròn (I) và (K) cắt nhau.
Phương pháp giải - Xem chi tiết
a) Chứng minh 3 điểm I, D, J thẳng hàng và \(IJ = ID + DJ\) suy ra hai đường tròn (I) và (J) tiếp xúc ngoài với nhau tại D.
b) + Do (K) và (I) có điểm chung là D nên chúng chỉ có thể cắt nhau hoặc tiếp xúc nhau.
+ Chứng minh (K) tiếp xúc với (I) là vô lí. Suy ra (K) và (I) là hai đường tròn cắt nhau.
Lời giải chi tiết
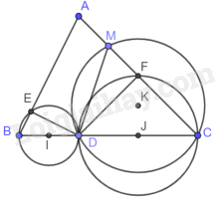
a) Tâm I của đường tròn ngoại tiếp tam giác vuông EBD là trung điểm của đoạn thẳng BD.
Tâm J của đường tròn ngoại tiếp tam giác vuông FDC là trung điểm của đoạn thẳng DC.
Vì D nằm trên BC nên ba điểm I, D, J thẳng hàng và \(IJ = ID + DJ\).
Suy ra, hai đường tròn (I) và (J) tiếp xúc ngoài với nhau tại D.
b) Do (K) và (I) có điểm chung là D nên chúng chỉ có thể cắt nhau hoặc tiếp xúc nhau.
Nếu (K) tiếp xúc với (I) thì D là tiếp điểm và K, I, D thẳng hàng, nghĩa là K thuộc đoạn DC và \(KD = KC\).
Vậy K phải trùng với trung điểm J của đoạn CD.
Điều đó nghĩa là đường tròn (K) trùng với đường tròn (J) và M trùng với F (trái với giả thiết).
Do đó, (K) và (I) là hai đường tròn cắt nhau.