Giải bài 15 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1 — Không quảng cáo

Đề bài

Cho tam giác ABC cân tại A, $\widehat A < {90^o}$. Vẽ đường tròn đường kính AB cắt BC và AC lần lượt tại D và E. Chứng minh rằng:

a) $\Delta DBE$ là tam giác cân.

b) $\widehat {CBE} = \frac{1}{2}\widehat {BAC}$

Lời giải chi tiết

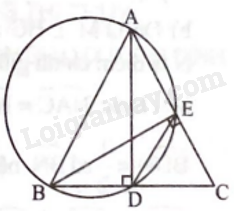
a) Ta có D, E cùng nằm trên đường tròn đường kính AB nên $\widehat {ADB} = \widehat {AEB} = {90^o}$ hay $AD \bot BC$ và $BE \bot AC$ .

Mà tam giác ABC cân tại A nên D là trung điểm BC nên DE = DB = DC. Vậy tam giác BDE cân tại D.

b) Ta có AD là tia phân giác của $\widehat {CAB}$ , nên $\widehat {BAD} = \widehat {CAD} = \frac{1}{2}\widehat {CAB}$ .

Mặt khác $\widehat{CBE}=\widehat{DBE}=\widehat{EAD}=\frac{1}{2}sđ\overset\frown{DE}$.

Suy ra $\widehat {CBE} = \widehat {BAD} = \frac{1}{2}\widehat {BAC}$ .