Giải bài 16 trang 101 sách bài tập toán 9 - Chân trời sáng tạo tập 1
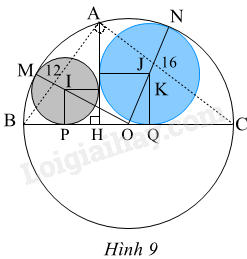
Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O). Tính: a) BC, BH. b) Bán kính R, R’ của đường tròn (I) và (J). c) Khoảng cách PQ.
Đề bài
Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O). Tính:
a) BC, BH.
b) Bán kính R, R’ của đường tròn (I) và (J).
c) Khoảng cách PQ.
Phương pháp giải - Xem chi tiết
Dựa vào: định lý Pytago để chứng minh.
Lời giải chi tiết
a) \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{12}^2} + {{16}^2}} = 20\).
\(\Delta BHA\backsim \Delta BAC\) suy ra BA 2 = BH.BC, suy ra BH = \(\frac{{B{A^2}}}{{BC}} = \frac{{36}}{5}.\)
b) \(OH = OB – BH = 10 - \frac{{36}}{5} = \frac{{14}}{5}.\)
Áp dụng định lí Pytago trong tam giác IPO vuông tại P, ta có
IO 2 = IP 2 + PO 2 , suy ra (10 – R) 2 = R 2 + \({\left( {R + \frac{{14}}{5}} \right)^2}\), suy ra R = \(\frac{{16}}{5}\).
Áp dụng định lí Pytago trong tam giác JQO vuông tại Q, ta có
JO 2 = JQ 2 + QO 2 ,
suy ra (10 – R’) 2 = R’ 2 + \({\left( {R' - \frac{{14}}{5}} \right)^2}\),
suy ra \(R’ = \frac{{24}}{5}\).
c) Ta có PQ = PH + QH = R + R’ = 8.