Giải bài 16 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2 — Không quảng cáo

Đề bài

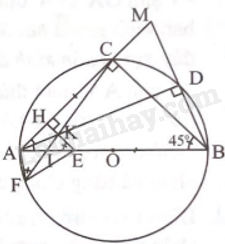
Cho đường tròn tâm O, đường kính AB. Gọi C là điểm chính giữa của cung AB. Trên đoạn thẳng AB lấy điểm E sao cho BE = AC. Tia AC và tia BD cắt nhau tại M. Vẽ EH vuông góc với AC tại H. Tia phân giác của góc \(\widehat {BAC}\) cắt EH tại K và cắt đường tròn (O) tại D. Tia CK cắt AB tại I và cắt đường tròn (O) tại F.

a) Chứng minh EH // BC.

b) Tính số đo của \(\widehat {AMB}\).

c) Chứng minh \(\widehat {AEK} = \widehat {AFK}\).

d) Chứng minh I là trung điểm của đoạn thẳng AE.

Lời giải chi tiết

a) Ta có \(\widehat {ACB} = {90^o}\)(góc nội tiếp chắn nửa đường tròn), suy ra \(BC \bot AC\).

Mà \(EH \bot AC\)(gt), suy ra EH // BC.

b) Vì AD là tia phân giác của \(\widehat {BAC}\) (gt) nên \(\widehat {CAD} = \widehat {BAD}\), suy ra \(s\overset\frown{CD}=s\overset\frown{BD}={{45}^{o}}.\)

Suy ra \(\widehat {MAB} = {45^o}\);

\(\widehat {MBA} = \widehat {MBC} + \widehat {CBA} = {22,5^o} + {45^o} = {67,5^o}\)

c) Vì EH // BC nên \(\widehat {AEK} = \widehat {ABC}\) (hai góc đồng vị).

Ta có \(\widehat {AFK} = \widehat {AFC} = \widehat {ABC}\) (cùng chắn cung AC).

Suy ra \(\widehat {AEK} = \widehat {AFK}\).

d) Tam giác AIC có AK là tia phân giác \(\widehat {CAI}\), suy ra \(\frac{{AI}}{{AC}} = \frac{{KI}}{{KC}}\)  (1).

Tam giác CIB có EK // CB suy ra \(\frac{{IE}}{{BE}} = \frac{{KI}}{{KC}}\) (2).

Từ (1) và (2) suy ra \(\frac{{AI}}{{AC}} = \frac{{IE}}{{BE}}\). Mà AC = BE (gt) nên AI = IE.

Vậy I là trung điểm của đoạn thẳng AE.