Giải bài 2 trang 87 vở thực hành Toán 9 tập 2
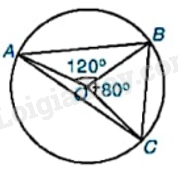
Cho các điểm như hình bên. Tính số đo các góc của tam giác ABC, biết rằng (widehat {AOB} = {120^o},widehat {BOC} = {80^o}).
Đề bài
Cho các điểm như hình bên. Tính số đo các góc của tam giác ABC, biết rằng \(\widehat {AOB} = {120^o},\widehat {BOC} = {80^o}\).
Phương pháp giải - Xem chi tiết
+ Vì góc ở tâm COB và góc nội tiếp CAB cùng chắn cung nhỏ BC nên \(\widehat {BAC} = \frac{1}{2}\widehat {COB}\).
+ Vì góc ở tâm AOB và góc nội tiếp ACB cùng chắn cung nhỏ AB nên \(\widehat {ACB} = \frac{1}{2}\widehat {AOB}\).
+ Tam giác ABC có: \(\widehat {ABC} = {180^o} - \widehat {BAC} - \widehat {ACB}\).
Lời giải chi tiết
Xét trong đường tròn (O), ta có:
\(\widehat {BAC} = \frac{1}{2}\widehat {COB} = {40^o}\) (góc ở tâm COB và góc nội tiếp CAB cùng chắn một cung $\overset\frown{BC}$);
\(\widehat {ACB} = \frac{1}{2}\widehat {AOB} = {60^o}\) (góc ở tâm AOB và góc nội tiếp ACB cùng chắn một cung $\overset\frown{AB}$).
Tổng ba góc trong tam giác ABC bằng \({180^o}\) nên \(\widehat {ABC} = {180^o} - \widehat {BAC} - \widehat {ACB} = {80^o}\).