Giải bài 2 trang 92 vở thực hành Toán 9 tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3cm. Tính diện tích tam giác ABC.
Đề bài
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3cm. Tính diện tích tam giác ABC.
Phương pháp giải - Xem chi tiết
+ Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Ta có: \(R = \frac{{\sqrt 3 }}{3}BC\) nên tính được BC.
+ Gọi M là trung điểm của BC nên \(AM = \frac{3}{2}AO\).
+ Diện tích tam giác ABC là: \(S = \frac{1}{2}AM.BC\).
Lời giải chi tiết
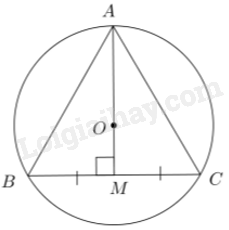
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Ta có: \(R = \frac{{\sqrt 3 }}{3}BC\), hay \(BC = \sqrt 3 R = 3\sqrt 3 cm\).
Gọi M là trung điểm của BC. Ta có: \(AM = \frac{3}{2}AO = \frac{9}{2}cm\).
Vậy \({S_{ABC}} = \frac{1}{2}AM.BC = \frac{{27\sqrt 3 }}{4}\;c{m^2}\).
Cùng chủ đề:
Giải bài 2 trang 92 vở thực hành Toán 9 tập 2