Giải bài 3 trang 71 SGK Toán 8 – Chân trời sáng tạo — Không quảng cáo

Đề bài

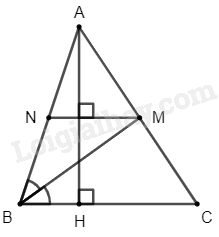
Cho tam giác nhọn $ABC$ có $AH$ là đường cao. Tia phân giác của góc $B$ cắt $AC$ tại $M$ . Từ $M$ kẻ đường thẳng vuông góc với $AH$ và cắt $AB$ tại $N$ . Chứng minh rằng:

a) Tứ giác $BCMN$ là hình thang

b) $BN = MN$

Lời giải chi tiết

a) Ta có:

$NM \bot AH$ (gt)

$BC \bot AH$ (gt)

Suy ra $NM$ // $BC$

Suy ra $BNMC$ là hình thang

b) Vì $NM$ // $BC$ (cmt)

Suy ra $\widehat {{\rm{NMB}}} = \widehat {{\rm{MBC}}}$ (so le trong)

Mà $\widehat {{\rm{MBN}}} = \widehat {{\rm{MBC}}}$ (do $MB$ là phân giác)

Suy ra $\widehat {{\rm{MBN}}} = \widehat {{\rm{NMB}}}$

Suy ra $\Delta MNB$ cân tại $N$

Suy ra $BN = NM$