Giải bài 3 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và (widehat {AMB} = {35^o}). a) Tính số đo của góc ở tâm tạo bởi hai bán kính OA, Ob. b) Tính số đo mỗi cung (oversetfrown{AB}) (cung lớn và cung nhỏ).
Đề bài
Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và \(\widehat {AMB} = {35^o}\) .
a) Tính số đo của góc ở tâm tạo bởi hai bán kính OA, OB.
b) Tính số đo mỗi cung \(\overset\frown{AB}\) (cung lớn và cung nhỏ).
Phương pháp giải - Xem chi tiết
Dựa vào: Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. Số đo của cung lớn bằng hiệu giữa 360 o và số đo cung nhỏ có chung hai đầu mút với cung lớn.
Lời giải chi tiết
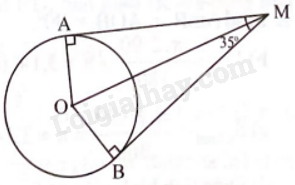
a) Vì MA, MB là hai tiếp tuyến của (O) cắt nhau tại M nên \(\widehat {OAM} = {90^o},\widehat {MBO} = {90^o}\).
Xét tứ giác AOBM, ta có: \(\widehat {OAM} + \widehat {OBM} + \widehat {AMB} + \widehat {AOB} = {360^o}\)
Hay \({90^o} + {90^o} + {35^o} + \widehat {AOB} = {360^o}\) suy ra \(\widehat {AOB} = {145^o}\).
b) Vì \(\widehat {AOB} = {145^o}\) nên số đo cung nhỏ \(\overset\frown{AB}\) là 145 o , số đo cung lớn \(\overset\frown{AB}\) là 360 o – 145 o = 215 o .