Giải bài 30 trang 100 sách bài tập toán 8 - Cánh diều — Không quảng cáo

Đề bài

Cho hình thoi $ABCD$ có $AB = 2$cm, $\widehat A = \frac{1}{2}\widehat B$. Các điểm $H,K$ thay đổi lần lượt trên cạnh $AD,CD$ sao cho $\widehat {HBK} = 60^\circ$.

a)     Chứng minh $DH + DK$ không đổi

b)    Xác định vị trí của các điểm $H,K$ để độ dài $HK$ ngắn nhất. Tính độ dài ngắn nhất đó.

Lời giải chi tiết

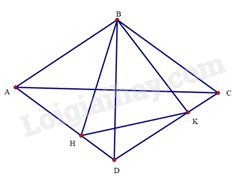
a)     Do $ABCD$ là hình thoi nên $AB = DA = 2cm,\widehat {ABD} = \widehat {CDB} = \frac{1}{2}\widehat {ABC}$

Mà $\widehat {BAD} = \frac{1}{2}\widehat {ABC}$, suy ra $\widehat {BAD} = \widehat {ABD}$. Do đó tam giác $ABD$ cân tại $D$. Suy ra $DA = DB$.

Mà $AB = DA$, suy ra $AB = DA = DB$.

$\Delta ABH = \Delta DBK$ (g.c.g). Suy ra $AH = DK$. Do đó $DH + DK = DH + AH = AD$.

Vậy $DH + DK$ không đổi

b)    Do $\Delta ABH = \Delta DBk$ nên $BH = BK$.

Tam giác $BHK$ có $BH = BK$ và $\widehat {HBK} = 60^\circ$ nên tam giác $BHK$ là tam giác đều.

Suy ra $HK = BH = BK$.

Do đó, độ dài $HK$ ngắn nhất khi $BH$ và $BK$ ngắn nhất. Vậy $H,K$ lần lượt là hình chiếu của $B$ trên $AD,CD$.

Khi đó $\Delta ABH = \Delta DBH$ (cạnh huyền – cạnh góc vuông)

Suy ra $AH = DH = \frac{{AD}}{2} = 1cm$

Trong tam giác $ABH$ vuông tại $H$, ta có: $A{B^2} = A{H^2} + B{H^2}$. Suy ra ta tính được $BH = \sqrt 3 cm$. Vậy độ dài ngắn nhất của $HK$ là $\sqrt 3$ cm.