Giải bài 30 trang 70 sách bài tập toán 8 – Cánh diều
Cho hình vuông \(ABCD\) cạnh bằng \(a\). Lấy điểm \(E\) thuộc cạnh \(BC\), điểm \(F\) thuộc cạnh \(AD\) sao cho \(CE=AF\). Các đường thẳng \(AE,BF\) cắt đường thẳng \(DC\) lần lượt tại \(M\) và \(N\).
Đề bài
Cho hình vuông \(ABCD\) cạnh bằng \(a\). Lấy điểm \(E\) thuộc cạnh \(BC\), điểm \(F\) thuộc cạnh \(AD\) sao cho \(CE=AF\). Các đường thẳng \(AE,BF\) cắt đường thẳng \(DC\) lần lượt tại \(M\) và \(N\). Các đường thẳng \(NA,MB\) cắt nhau tại \(K\).
a) Chứng minh: \(\Delta KAB\backsim \Delta KNM;\Delta CEM\backsim \Delta DAM;\Delta NFD\backsim \Delta NBC\).
b) So sánh \(CM.DN\) và \(A{{B}^{2}}\).
c) Các điểm \(E,F\) lấy ở vị trí nào trên các cạnh \(BC,AD\) thì \(MN\) có độ dài nhỏ nhất?
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của hai tam giác đồng dạng:
- Mỗi tam giác đồng dạng với chính nó
Nếu \(\Delta A'B'C'\backsim \Delta ABC\) thì \(\Delta ABC\backsim \Delta A'B'C'\).
Nếu \(\Delta A''B''C''\backsim \Delta A'B'C'\) và \(\Delta A'B'C'\backsim \Delta ABC\) thì \(\widehat{A}=\widehat{A''},\widehat{B}=\widehat{B''},\widehat{C}=\widehat{C''}\).
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết
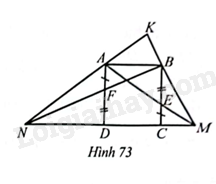
a) Vì \(AB//MN\) nên \(\Delta KAB\backsim \Delta KMN\).
Vì \(CE//AD\) nên \(\Delta CEM\backsim \Delta DAM\)
Vì \(DF//BC\) nên \(\Delta NFD\backsim \Delta NBC\).
b) Vì \(\Delta CEM\backsim \Delta BEA\) nên \(\frac{CM}{BA}=\frac{CE}{BE}\) (1)
Vì \(\Delta NDF\backsim \Delta BAF\) nên \(\frac{AF}{FD}=\frac{BA}{DN}\) (2)
Từ (1) và (2) và \(CE=AF,BE=DF\), ta có \(\frac{CM}{BA}=\frac{CE}{BE}=\frac{AF}{FD}=\frac{BA}{DN}\).
Do đó \(CM.DN=A{{B}^{2}}\).
c) Ta có \({{\left( CM-DN \right)}^{2}}\ge 0\), suy ra \({{\left( CM+DN \right)}^{2}}\ge 4CM.DN\) hay \(CM+DN\ge 2\sqrt{CM.DN}=2AB\). Do đó \(MN=DN+CD+CM\ge 3AB\) (vì \(AB=CD\)). Vậy \(MN\) có độ dài nhỏ nhất bằng \(3AB\). Dấu “=” xảy ra khi \(CM=DN=a\) hay \(E,F\) lần lượt là trung điểm của \(BC\) và \(AD\).