Giải bài 31 trang 63 sách bài tập toán 8 - Cánh diều — Không quảng cáo

Đề bài

Trong mặt phẳng tọa độ $Oxy$, cho các điểm $A\left( {2;3} \right),B\left( {2; - 4} \right)$. Tìm tọa độ điểm $C$ sao cho $C$ nằm trên trục $Ox$ và $CA + CB$ đạt giá trị nhỏ nhất.

Lời giải chi tiết

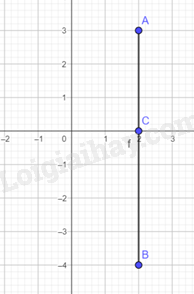
Ta có: $CA + CB \ge AB$ nên $CA + CB$ đạt giá trị nhỏ nhất bằng $AB = 7$. Khi đó, $C$ là giao điểm của $AB$ và trục $Ox$. Vậy $C\left( {2;0} \right)$.